Системи лінійних рівнянь: основні означення та поняття.

Лекція 3.

Системи лінійних рівнянь

План

1. Поняття про системи лінійних рівнянь та їх розв’язки.

2. Розв’язування системи лінійних рівнянь методом послідовного виключення невідомих (метод Гаусса).

3. Розв’язування системи лінійних рівнянь за правилом Крамера.

4. Матричний метод розв’язування систем лінійний рівнянь

Література:

Рудницький . Вища математика. Ст. 49-65

Барковський В.В. Барковська Н.В. “Вища математика для економістів” Ст. 99-110

Основні поняття і терміни: система лінійних рівнянь, основна матриця системи, розширена матриця системи, однорідна система лінійних рівнянь, сумісність системи, теорема Кронекера-Капеллі, метод Гауса, метод Крамера, матричний метод.

Системи лінійних рівнянь: основні означення та поняття.

В загальному випадку система 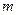лінійних рівнянь з 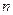невідомими має такий вигляд

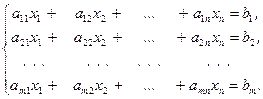(2.1)

або

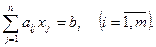
Кожній системі можна співставити дві матриці:

основну матрицю системи, елементами якої є коефіцієнти при невідомих

.

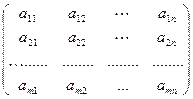розширену матрицю системи , яку дістаємо з основної добавленням стовпця вільних членів

.

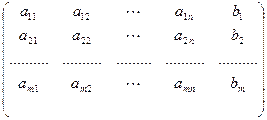Зауваження.Подамо загальне правило запису систем лінійних алгебраїчних рівнянь.

Невідомі позначають однією буквою і відрізняють їх за індексами, наприклад .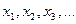

Коефіцієнти біля невідомих позначають однією будь-якою буквою з двома індексами. Перший індекс вказує номер рівняння, другий – номер невідомого , біля якого стоїть даний коефіцієнт.

Вільні члени позначають будь-якою буквою з одним індексом, який вказує на номер рівняння.

Систему лінійних рівнянь називають однорідною, якщо всі її вільні члени 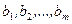дорівнюють нулю. Якщо принаймні один з її вільних членів 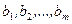відмінний від нуля, то система називають неоднорідною.

Систему (2.1) називають квадратною, якщо число 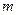її рівнянь дорівнює числу 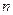її невідомих.

Означення Розв’язком системи називається така сукупність чисел 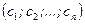, яка при підстановці в систему на місце невідомих 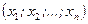перетворює всі рівняння системи в тотожності.

Систему рівнянь називають сумісною, якщо вона має принаймні один розв’язок, і несумісною, якщо вона не має жодного розв’язку.

Сумісну систему називають визначеною, якщо вона має один розв’язок і невизначеною, якщо у неї принаймні два різних розв’язки.

Питання про сумісність систем розв’язується за допомогою теореми Кронекера-Капеллі.

Теорема (Кронекера-Капеллі). Для того щоб система 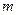лінійних алгебраїчних рівнянь з 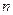невідомими була сумісна, необхідно і достатньо, щоб ранг основної матриці системи і ранг розширеної матриці системи були рівні

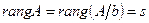
Дальше, якщо 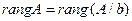і 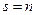, то система має єдиний розв’язків; якщо 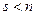, то система має безліч розв’язків.

Основними методами розв’язування систем лінійних рівнянь є : метод Гауса, метод Крамера та метод оберненої матриці.