Система лінійних рівнянь сумісна тоді й лише тоді, коли ранг r основної матриці системи дорівнює рангу розширеної матриці цієї системи.

За цією теоремою, якщо ранги основної та розширеної матриць не рівні, то система несумісна й немає сенсу її розв’язувати. Якщо ранги матриць рівні, то система сумісна.

Для сумісних лінійних рівнянь можливі такі випадки.

1. Якщо ранг матриці сумісної системи дорівнює числу невідомих, тобто r=n, то система (1) має єдиний розв’язок.

2. Якщо ранг матриці сумісної системи менший від числа невідомих, тобто 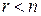, то система невизначена й має нескінченну кількість розв’язків.

Нехай 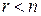; тоді r невідомих x₁, x₂, ¼, x_r називаються основними, або базисними, якщо визначник матриці з коефіцієнтів при цих невідомих відмінний від нуля. Решта n-r невідомих називаються неосновними, або вільними. Оскільки вільні невідомі можуть набувати довільних значень, то в цьому разі система буде невизначеною.

Розв’язок (1), в якому всі n-r неосновних невідомих дорівнюють нулю, називають базисним.

Однорідні системи. Фундаментальна система розв’язків СЛАР

Система m лінійних рівнянь з n невідомимими називається системою лінійних однорідних рівнянь, якщо всі вільні члени дорівнюють нулеві:

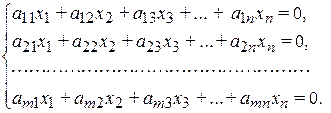, (5)

Якщо у системі (5) т=п, а її визначник відмінний від нуля, то така система має тільки нульовий розв’язок. Ненульові розв’язки можливі лише для таких систем лінійних однорідних рівнянь, у яких число рівнянь менше за число змінних або дорівнює їм, коли визначник системи дорівнює нулеві.

Отже, система лінійних однорідних рівнянь має ненульові розв’язки тоді і тільки тоді, коли ранг її матриці коефіцієнтів при змінних менший за число змінних, тобто при .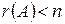

Позначимо розв’язок системи (5) 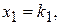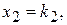…, 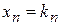у вигляді рядка .

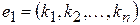Розв’язки системи лінійних однорідних рівнянь мають такі властивості:

1. Якщо рядок 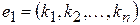- розв’язок системи (5), то і рядок 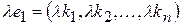- також розв’язок цієї системи.

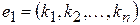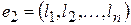2. Якщо рядки і - розв’язки системи (5), то при будь-яких 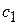і 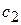їх лінійна комбінація 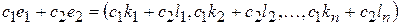- також розв’язок даної системи.

Із сформульованих властивостей випливає, що будь-яка лінійна комбінація розв’язків системи лінійних однорідних рівнянь також є розв’язком цієї системи.

Означення. Система лінійно незалежних розв’язків 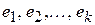називається фундаментальною, якщо кожен розв’язок системи (5) є лінійною комбінацією розв’язків .

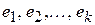Теорема. Якщо ранг 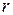матриці коефіцієнтів при змінних системи лінійних однорідних рівнянь (5) менший за число змінних п, то будь-яка фундаментальна система розв’язків системи (5) складається із 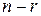розв’язків.

Тому загальний розв’язок системи (5) лінійних однорідних рівнянь має вигляд:

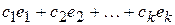, (6)

де 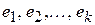- будь-яка фундаментальна система розв’язків, 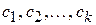- довільні числа і .

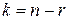Отже, загальний розв’язок системи т лінійних рівнянь з п змінними (1) дорівнює сумі загального розв’язку відповідної їй системі однорідних лінійних рівнянь (5) і довільного частинного розв’язку цієї системи (5).