Тема 5, 6. Лінійні однорідні диференціальні рівняння другого порядку зі сталими коефіцієнтами. Задача Коші.

Для диференціальних рівнянь другого порядку, як і для рівнянь першого порядку, розглядається задача Коші або задача з початковими умовами. Для рівняння (1) ця задача ставиться так: серед усіх розв’язків рівняння (1) знайти такий розв’язок 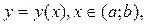який при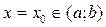

задовольняє такі умови:

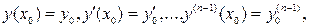
або ( 6 )

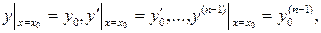
де 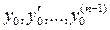- довільні наперед задані дійсні числа.

Умови ( 6 ) називають початковими умовами рівняння ( 1 ). Зокрема, рівняння другого порядку

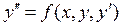
початкові умови при х= х₀ мають вигляд

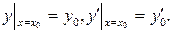
Існування і єдність розв’язку задачі Коші визначають такою теоремою Коші.

Теорема 2.Якщо функція 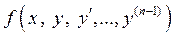і її похідні по аргументам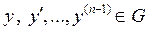 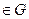то для будь – якої точки 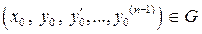існує єдиний розв’язок 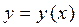рівняння (1), який задовольняє початкові умови (6).

Приклад .

Знайти розв’язок задачі Коші:

а) ;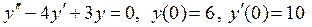

б) .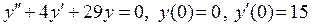

Розв’язання:

а) Складемо характеристичне рівняння 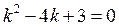і знайдемо його корені 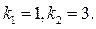За формулою ( 3 ) шуканий розв’язок має вигляд:

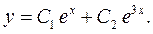
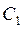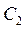Знайдемо та , використовуючи початкові умови:

Знайдемо :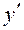

.

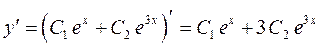
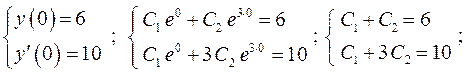
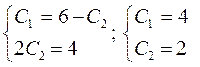Отже, 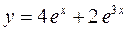– розв’язок рівняння , який задовольняє дані початкові умови.

б) Складемо характеристичне рівняння 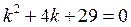і знайдемо його корені 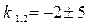За формулою ( 4 ) шуканий розв’язок має вигляд:

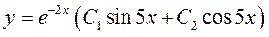
Знайдемо 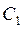та 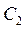, використовуючи початкові умови:

Знайдемо : ;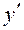

.

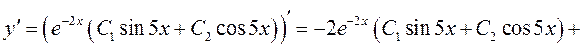
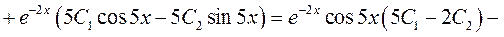
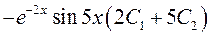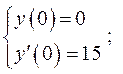
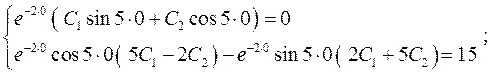
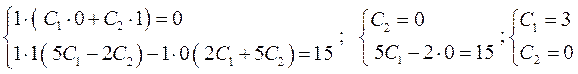Отже, 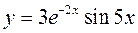– розв’язок рівняння , який задовольняє дані початкові умови.

ПИТАННЯ ТА ЗАВДАННЯ ДЛЯ

САМОСТІЙНОГО

ОПРАЦЮВАННЯ МАТЕРІАЛУ

Тема 1. Рівняння Бернуллі.

Завдання для самоконтролю:

1.1. Розв’язати рівняння Бернуллі .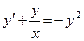

Питання для самоконтролю:

1. Загальний вигляд рівняння Бернуллі.

2. Структура розв’язку рівняння Бернуллі.

Тема 2, 3. Розв’язання диференціальних рівнянь, що дозволяють знизити порядок.

Завдання для самоконтролю:

3.1. Розв’язати рівняння .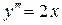

3.2. Розв’язати рівняння .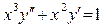

3.3. Розв’язати рівняння .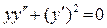

Питання для самоконтролю:

1. Види диференціальних рівнянь, що дозволяють знизити порядок.

2. Способи розв’язання диференціальних рівнянь, що дозволяють знизити порядок, в залежності від виду.

Тема 4. Лінійні однорідні диференціальні рівняння другого порядку зі сталими коефіцієнтами.

Завдання для самоконтролю:

4.1. Розв’язати рівняння .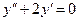

4.2. Розв’язати рівняння .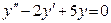

4.3. Розв’язати рівняння .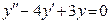

Питання для самоконтролю:

1. Що називається характеристичним рівнянням.

2. Загальний розв’язок однорідні диференціальні рівняння другого порядку, у випадку дійсних та різних коренів характеристичного рівняння.

3. Загальний розв’язок однорідні диференціальні рівняння другого порядку, у випадку дійсних рівних коренів характеристичного рівняння.

4. Загальний розв’язок однорідні диференціальні рівняння другого порядку, у випадку комплексно спряжених коренів характеристичного рівняння.