Частотные методы идентификации динамических объектов.
Динамические свойства объекта могут быть описаны с помощью частотных характеристик, которые представляют собой зависимость от частоты в установившемся режиме двух переменных: 1) отношение амплитуд гармонических сигналов на вход и выход объекта – это АЧХ; 2) сдвиг фаз между входным и выходным сигналами – это ФЧХ. Указанные характеристики изображаются в 2-х форматах: 1) в виде совокупности АЧХ и ФЧХ в прямоугольной системе координат (форма Боде); 2) характеристик строиться в полярных координатах в комплексной плоскости и представляет амплитудно-фазовую характеристику (АФХ) или динамику Найквиста.
Если в диаграмме Боде А(  ) заменяется на L(
) заменяется на L( 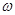 ), то характеристика называется логарифмо-частотной характеристикой (ЛЧХ)
), то характеристика называется логарифмо-частотной характеристикой (ЛЧХ)
Заданные аналитически или графически частотные характеристик объекта позволяют рассчитать контур стабилизации со стандартным регулятором, например: с ПИ или ПИД законом регулирования.
Эксперимент, с помощью которого исследуются частотные характеристики значительно трудоемок на аппаратуре и времени проведения по сравнению с переходными характеристиками. Для исследования необходима аппаратура с помощью которой на вход объекта можно подать гармонический сигнал. Выходной сигнал как правило всегда зашумлен и искажен нелинейностями, имеющимися в объекте. Поэтому для определения амплитуды и фазы выходного гармонического сигнала необходимо выделение 1-ой гармонической составляющей вручную или с помощью спец. аппаратуры. Исследование на различных в том числе и низких частотах требует много времени. Поскольку при исследовании частотных характеристик рассматриваются вынужденные, а не свободные движения системы, то необходимо некоторое время для затухания свободного движения.
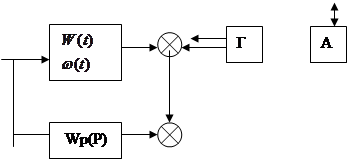
На исследование частотных характеристик неблагоприятное влияние оказывают тренды, вызывающие выползание средней линии выходного сигнала. Для уменьшения ошибок из-за выползания средней линии и уменьшения влияния помех снятия частотных характеристик проводят в замкнутой системе приведенной на рис. 1., где объект охвачен обратной связью с регулятором.
|
 Y(t)
Y(t) 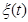
x(t)
y(t)
Рис.1.
На анализатор А, выделяющий первые гармонические составляющие подаются на входные и выходные сигналы объекта управления. Полученные таким образом частотные характеристики могут быть непосредственно использованы для расчета системы управления.
Частотный метод по сравнению с временным имеет ряд преимуществ:
1) при снятии частотных характеристик объект исследуется в установившемся, а не переходном режиме, поэтому влияние случайных помех на результаты будут сказываться меньше;
2) соответствующим выборам амплитуды входных колебаний можно установить достаточно большие колебания регулируемых величин, при которых погрешности измерительных приборов будут мало сказываться.
Вместе с тем частотный метод имеет и отрицательные стороны:
1) длительность эксперимента;
2) большая трудоемкость в обработке полученных результатов.
Для уменьшения затрат времени на снятия частотных характеристик и их обработку применяют специальное оборудование, содержащее генератор синусоидальных колебаний и вычислительные устройства для выделения 1-х гармоник и выполнения расчетов.

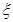 (t) могут содержать кроме случайных составляющих и детерминированные тренды. Но в сигнале Y(t) уползание будет устранено, а воздействие случайных составляющих на выходе
(t) могут содержать кроме случайных составляющих и детерминированные тренды. Но в сигнале Y(t) уползание будет устранено, а воздействие случайных составляющих на выходе