Основные свойства б.м. и б.б. последовательностей

Основные числовые множества

N	{1,2,3,...,n} Множество всех натуральных чисел
Z	{0, ±1, ±2, ±3,...} Множество целых чисел.Множество целых чисел включает в себя множество натуральных.
Q	Множество рациональных чисел. Кроме целых чисел имеются ещё и дроби. Дробь — это выражение вида , где p — целое число, q — натуральное. Десятичные дроби также можно записать в виде . Например: 0,25 = 25/100 = 1/4. Целые числа также можно записать в виде . Например, в виде дроби со знаменателем "один": 2 = 2/1. Таким образом любое рациональное число можно записать десятичной дробью — конечно или бесконечной периодической.
R	Множество всех вещественных чисел. Иррациональные числа — это бесконечные непериодические дроби. К ним относятся: § число — отношение длины окружности к её диаметру; § число — названное в честь Эйлера и др.; Вместе два множества (рациональных и иррациональных чисел) — образуют множество действительных (или вещественных) чисел.

Операции над множествами

Два множества А и В равны (А=В), если они состоят из одних и тех же элементов.
Например, если А={1,2,3,4}, B={3,1,4,2} то А=В.

Объединением (суммой)множеств А и В называется множество А ∪ В, элементы которого принадлежат хотя бы одному из этих множеств.
Например, если А={1,2,4}, B={3,4,5,6}, то А ∪ B = {1,2,3,4,5,6}

Пересечением (произведением) множеств А и В называется множество А ∩ В, элементы которого принадлежат как множеству А, так и множеству В.
Например, если А={1,2,4}, B={3,4,5,2}, то А ∩ В = {2,4}

Разностью множеств А и В называется множество АВ, элементы которого принадлежат множесву А, но не принадлежат множеству В.
Например, если А={1,2,3,4}, B={3,4,5}, то АВ = {1,2}

Симметричной разностью множеств А и В называется множество А Δ В, являющееся объединением разностей множеств АВ и ВА, то есть А Δ В = (АВ) ∪ (ВА).
Например, если А={1,2,3,4}, B={3,4,5,6}, то А Δ В = {1,2} ∪ {5,6} = {1,2,5,6}

Свойства операций над множествами

Свойства перестановочности

A ∪ B = B ∪ A
A ∩ B = B ∩ A

Сочетательное свойство

(A ∪ B) ∪ C = A ∪ (B ∪ C)
(A ∩ B) ∩ C = A ∩ (B ∩ C)

2 Понятие функции. Способы задания функции. Элементарные функции.

Функцией называется закон, по которому числу х из заданного множества Х, поставлено в соответствие только одно число у, пишут , при этом x называют аргументом функции, y называют значением функции.

1. Способы задания функции

Задать функцию означает установить правило (закон) с помощью которого по данным значениям независимой переменной находим соответствующие им значения функции. Рассмотрим различные способы задания функции.

1. Табличный способ.При этом способе в определенном порядке выписываются ряд значений независимой переменной и соответствующие им значения функции . Таковы, например, таблицы логарифмов, таблицы значений тригонометрических функций и т.д. Табличный способ очень распространен в технике, естествознании и т.п. Численные результаты последовательных наблюдений какого-либо процесса или явления выписываются в виде таблицы. Например, результаты измерений температуры воздуха на метеорологической станции за один день оформляются так:

t, ч
Т, °С	-1	-2	-2,5	-2	-0,5				3,5

Эта запись определяет температуру Т как функцию от времени t:T=f(t). Преимущества табличного способа задания функции состоят в том, что он дает возможность определить те или другие конкретные значения функции сразу, без дополнительных изменений или вычислений. Недостатки: определяет функцию не полностью, а лишь для некоторых значений аргумента; не дает наглядного изображения характера изменения функции с изменением аргумента.

2. Графический способ.Графикомфункцииy=f(x) называется множество всех точек плоскости, координаты которых удовлетворяют данному уравнению. Это может быть некоторая кривая, в частности прямая, множество точек на плоскости.

Преимущество – наглядность, недостаток – нет возможности точно определить значения аргумента. В технике и физике часто он является единственно доступным способом задания функции, например, при пользовании самопишущими приборами, которые автоматически записывают изменение одной величины относительно другой (барограф, термограф и др.).

3. Аналитический способ.По этому способу функция задается аналитически, с помощью формулы. Такой способ дает возможность по каждому численному значению аргумента х найти соответствующее ему численное значение функции у точно или с некоторой точностью.

При аналитическом способе функция может быть задана и несколькими разными формулами. Например, функция

задана в области определения [- , 15] с помощью трех формул.

Если зависимость между х и у задана формулой, разрешенной относительно у, т.е. имеет вид у = f(x) , то говорят, что функция от х задана в явном виде, например, . Если же значения х и у связаны некоторым уравнением видаF(x,y) = 0, т.е. формула не разрешена относительно у, то говорят, что функция задана неявно. Например, . Заметим, что не всякую неявную функцию можно представить в виде у =f(x), наоборот, любую явную функцию всегда можно представить в виде неявной: . Еще одна разновидность аналитического задания функции – параметрическое, когда аргумент х и функция у являются функциями третьей величины – параметраt: , где , Т – некоторый промежуток. Такой способ широко применяется в механике, в геометрии.

Аналитический способ является самым распространенным способом задания функции. Компактность, возможность применения к данной функции аппарата математического анализа, возможность вычисления значений функции при любых значениях аргумента – его основные преимущества.

4. Словесный способ.Этот способ состоит в том, что функциональная зависимость выражается словами. Например, функция Е(х) – целая часть числа х, функция Дирихле, функция Римана,n!,r(n) – число делителей натурального числаn.

5. Полуграфический способ.Здесь значения функции представляются в виде отрезков, а значения аргумента – в виде чисел, проставленных на концах отрезков, указывающих значения функции. Так, например, в термометре есть шкала с равными делениями, у которых проставлены числа. Эти числа являются значениями аргумента (температуры). Они стоят на том месте, которое определяет графическое удлинение столбца ртути (значения функции) в связи с ее объемным расширением в результате температурных изменений.

3 Аксиоматическое определение множества действительных чисел.

О п р е д е л е н и е . Совокупность элементов x, y, z, …, состоящая более чем из одного элемента, называется множеством R действительных чисел, если для этих объектов установлены следующие операции и отношения:

I. Для определено единственное числоa + b, называемое суммой двух действительных чисел, так что выполняются условия:

1) a + b = b + a – свойство коммутативности операции сложения;

2) a + b + c =(a + b) + c — свойство ассоциативности операции сложения;

3) $ число ноль такое, чтоa + 0= a для
0 – этонейтральный элемент операции сложения;

4) для $ противоположное число такое, что a + (–a)= 0;

5) число a + (–b) = a – b называется разностью чисел a и b.

II. Для определено единственное числоa·b (или ab), называемое произведением двух действительных чисел, так что выполняются условия:

1) a·b = b·a – свойство коммутативности операции умножения;

2) a·b·c =(a·b)·c – свойство ассоциативности операции умножения;

3) $ число единица такое, чтоa·1= a для
1 – этонейтральный элемент операции умножения;

4) для единственное обратное число такое, что ;

5) число (илиa : b) называется частным от деления числа a на число b.

III. Имеет место свойство дистрибутивности произведения относительно суммы:

(a + b)·c = a·c + b·c для .

IV. Упорядоченность множества действительных чисел .

Для имеет место одно и только одно отношение порядка:

a<bилиa=bилиa>b. При этом выполняются условия:

1) если a<bиb<c, тоa<c— транзитивность;

2) если a<b, тоa+c<b+cдля ;

3) если a <bиc > 0, тоa·c <b·c.

Как следствие этих условий получается свойство плотности множества действительных чисел :

Для и a < b $ число .

w такое, что a < c < b v

Отношения порядка называются неравенствами или сравнениями действительных чисел.

Нестрогие неравенства:

V. Непрерывность множества действительных чисел :

Для " непустых множеств и , у которых для и выполняется неравенство , существует такое число , что выполняется соотношение для и для (рис. 12).

4 Аксиома полноты. Лемма о вложенных отрезках.

Аксиома непрерывности (полноты). Каковы бы ни были непустые множества и , такие что для любых двух элементов и выполняется неравенство , существует такое действительное число , что для всех и имеет место соотношение

Геометрически, если трактовать действительные числа как точки на прямой, данное утверждение представляется очевидным. Если два множества 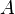и таковы, что на числовой прямой все элементы одного из них лежат левее всех элементов второго, то найдется число , разделяющее эти два множества, то есть лежащее правее всех элементов 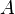(кроме, возможно, самого ) и левее всех элементов (та же оговорка).

Здесь следует отметить, что несмотря на «очевидность» данного свойства, для рациональных чисел оно не всегда выполняется. Для примера, рассмотрим два множества:

Легко видеть, что для любых элементов и выполняется неравенство . Однако рационального числа , разделяющего эти два множества, не существует. В самом деле, этим числом может быть только , но оно не является рациональным.

Лемма о вложенных отрезках

Формулировка

Для всякой системы вложенных отрезков

существует хотя бы одна точка , принадлежащая всем отрезкам данной системы.

Если, кроме того, длина отрезков системы стремится к нулю:

то — единственная общая точка всех отрезков данной системы.

Замечание

Отрезки в формулировке теоремы нельзя заменить на открытые интервалы. Например,

Доказательство

1) Существование общей точки. Множество левых концов отрезков лежит на числовой прямой левее множества правых концов отрезков , поскольку

В силу аксиомы непрерывности, существует точка , разделяющая эти два множества, то есть

в частности

Последнее неравенство означает, что — общая точка всех отрезков данной системы.

2) Единственность общей точки. Пусть длина отрезков системы стремится к нулю. Покажем, что существует только одна точка, принадлежащая всем отрезкам системы. Предположим противное: пусть имеется две различные точки и , принадлежащие всем отрезкам системы:

Тогда для всех номеров выполняются неравенства:

В силу условия стремления к нулю длин отрезков для любого для всех номеров , начиная с некоторого будет выполняться неравенство

Взяв в этом неравенстве , получим

Противоречие. Лемма доказана полностью.

5 Последовательность. Бесконечно малые и бесконечно большие последовательности.

Числовая последовательность — это последовательность элементов числового пространства.

Последовательность называется бесконечно малой последовательностью (б.м.п.), если для любого существует номер такой, что для любого выполняется неравенство:

Последовательность называется бесконечно большой (б.б.п.), если для любого существует номер такой, что для любого выполняется неравенство:

6 Свойства бесконечно малых последовательностей.

Основные свойства б.м. и б.б. последовательностей

1° Сумма б.м. последовательностей есть б.м.п.

2° Произведение ограниченной последовательности и б.м. есть б.м.п.

3° Если - б.м.п., то - ограниченная последовательность.

4° Произведение б.м.п. есть последовательность б.м.

5° Если - б.м.п. и , то , т.е.

6° Если - б.м.п. и , то последовательность - б.б.п.

7° Если - б.б.п., то и последовательность - б.м.п.

7 Сходящиеся последовательности. Предел сходящейся последовательности. Теорема об ограниченности сходящейся последовательности.

Определение: Последовательность {xn} называется сходящейся, если существует такое число а, что последовательность {xn-а} является бесконечно малой. При этом число а называется пределом последовательности {xn}.

В соответствии с этим определением всякая бесконечно малая последовательность является сходящейся и имеет своим пределом число ноль.