Независимость случайных событий.

Для полного обоснования теории вероятностей нам недостает еще одного основного понятия – понятия независимости событий.

При совместном рассмотрении двух случайных событий А и В часто возникает вопрос: насколько связаны эти события друг с другом, в какой мере наступление одного из них влияет на возможность наступления другого?

Простейшим примером связи между двумя событиями может служить причинная связь - когда наступление одного из событий ведет к обязательному осуществлению другого или же, наоборот. Однако наряду с такими крайними случаями существует и много промежуточных, когда непосредственная причинная зависимость одного события от другого отсутствует, но некоторая зависимость всё же имеется.

Для пояснения сказанного приведём пример.

Бросается игральная кость. Событие А – выпадение чётного числа очков, событие В – выпадение числа очков большего, чем 3. очевидно, было бы неверно утверждать, что одно из этих событий влечет за собой другое. В то же время между событиями А и В имеется какая-то зависимость. В самом деле, из трёх случаев, к которым сводится В (выпадение 4, 5 или 6 очков), событию А будут благоприятны два; поэтому, если считать наступившим событие В, то шансы события А будут 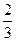. В то же время, при отсутствии предварительной информации об исходе бросания, шансы события А оцениваются отношением 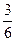. Так как 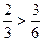, то следует признать, что наступление события В повышает шансы события А. Если мы введём в рассмотрение событие С – выпадение нечётного числа очков, то если мы будем считать наступившим событие С, то шансы наступления события А сведутся к нулю.

Для характеристики зависимости одних событий от других вводят понятие условной вероятности.

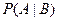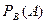Определение 1. Пусть А и В – два случайных события по отношению к некоторому опыту. Условной вероятностью события А при условии, что наступило событие В (обозначение или ) называется вероятность наступления события А при условии, что наступило

событие В.

Замечание. В §2 мы видели, что для вычисления вероятности события А важно, чтобы опыт производился при некотором комплексе условий, не меняющимся при повторении опыта; только в этом случае относительная частота 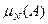появления события А будет «устойчива» - близка к некоторому числу Р(А) при больших N. Если комплекс условий изменить добавочным условием:некоторое событие B заведомо осуществилось, то новый комплекс условий определяет, по существу, уже другой опыт, и вероятность события в этом другом опыте, как правило, будет другой. Исходя из этого, можно дать общее определение условной вероятности

Определение 2. Пусть к комплексу условий, определяющим опыт, добавлено условие, что в опыте непременно осуществляется некоторое событие В; этим определяется некоторый новый опыт. Вероятность события А в таком новом опыте называется условной вероятностью события А при условии, что наступило событие В.

Выведем формулу для условной вероятности, исходя из только что сказанного.

Пусть опыт произведен N раз, но во внимание приняты лишь те случаи, когда наступило событие В. Тогда отношение 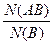показывает, какую долю от числа опытов, в которых наступило событие В, составляет число таких опытов, в которых, помимо В, наступило также и событие А. Таким образом, относительная частота 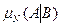события А в N опытах при условии, что наступило событие В равна

.

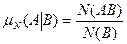Исходя из определения вероятности (см. §2) мы получаем, что условная вероятность события А при условии, что событие В наступило, равна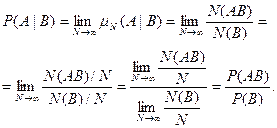

Итак, мы получили формулу для условной вероятности

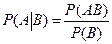. (1)

Замечание. При выводе формулы (1) естественно требовать условие, чтобы .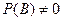

Из равенства (1) следует формула

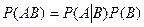, (2)

называемая формулой умножения вероятностей.

Замечание. Вероятность Р(А) ещё называют безусловной вероятностью события А.

Аналогично выводится формула

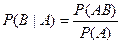(3)

(в случае, когда 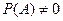) и тогда формула (2) будет выглядеть следующим образом

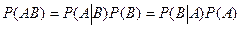. (4)

Пример 1. В урне находится m-белых и n-m не белых шаров. Последовательно, без возвращения выбираются два шара. Найдем вероятность того, что оба шара будут белыми.

Решение. Эту вероятность можно найти с помощью формулы умножения (2).

Обозначим событие 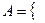первый вынутый шар - белый 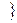, 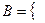второй вынутый шар - белый 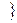. Тогда вычисление вероятносте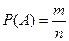й и 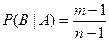сводится к более простым задачам о вынимании шара из урны, содержащей m белых и n-m не белых (см §6). Окончательно вероятность того, что оба шара будут белыми (события АВ) будет равна

.

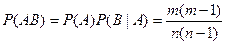С помощью (2), по индукции, легко доказывается более общая теорема.

Теорема (формула умножения). Пусть события А₁,…,А_n таковы, что 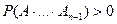. Тогда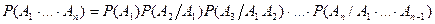

Пример 2. Слово «лотос», составленное из букв-кубиков, рассыпано на отдельные буквы, которые затем сложены в коробке. Из коробки наугад извлекают одну за другой три буквы. Какова вероятность того, что при этом появится слово «сто».

Решение. Введём обозначения для этих событий:

А ₁ – первой извлечена буква «С»;

А ₂ – второй извлечена буква «Т»;

А ₃ – третьей извлечена буква «О»;

А – получить слово «сто».

Очевидно, 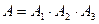. Тогда имеем последовательно:

;

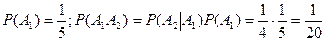И значит:

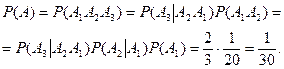
Теперь, опираясь на понятие условной вероятности, можно дать определение независимости событий, имеющего решающее значение для всех применений теории вероятности.

Мы уже видели на примерах, что вероятности Р(A) и 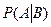, вообще говоря, различны; другими словами, наступление события В может изменить вероятность наступления события A. В связи с этим вводится следующее определение

Определение 3. Если 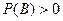, то мы говорим, что событие А не зависит от события В, если выполняется равенство

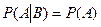. (5)

Таким образом, A не зависит от В, если наступление В не оказывает влияние на вероятность A (или, другими словами, наступление события В не меняет шансов наступления события A).

Если 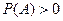, то в этом случае (когда наступление события А не зависит от наступления события В) получаем (см (3))

.

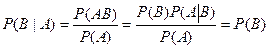Значит из независимости А от В следует независимость В от А, т.е. понятие независимости А и В симметрично.

Из формулы умножения вероятностей (2) следует, что для независимых событий A и В имеет место равенство:

.

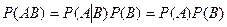Это приводит нас к следующему определению независимости:

Определение 4. События A и В называются независимыми, если

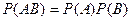. (6)

Если равенство (6) не выполняется, то события A и В будем называть зависимыми.

Это определение уже не содержит ограничений типа 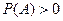и 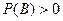. В частности, если 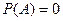, то из того, что событие АВ есть следствие события А следует, что и 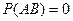, а тогда в силу (6) события A и В независимы. Из определения (6) следует, что 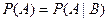и 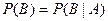, если эти условные вероятности существуют (т.е. 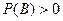и 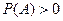соответственно). Таким образом, из определения 4 следует определение 3.

В дальнейшем мы будем пользоваться и тем, и другим определениями независимости событий (чаще всего определением 4).

Замечание. Обычно независимость событий A и В не устанавливается с помощью равенства (6), а постулируется на основе каких-либо внешних (интуитивных) соображений.

Обычный ход рассуждений таков: из конкретных условий рассматриваемого опыта делается заключение о (причинной) независимости тех или иных событий и затем с помощью равенства (6) мы вычисляем вероятность Р(АВ), зная вероятности Р(A) и Р(В) двух независимых событий.

Следующий пример показывает, что независимость может исчезнуть, если незначительно изменить вероятностную модель (схему).

Пример 3. Из колоды в 52 карты (состоящей из 13 карт каждой из четырёх мастей) наугад вынимается карта. Рассмотрим события A ={вынут туз} и В ={вынута карта червовой масти}. Тогда событие АВ={вынут туз червовой масти}. Тогда в этом случае получаем

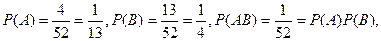
И значит события А и В независимы, хотя это и интуитивно ясно, что А не зависит от В (цена карты не зависит от масти).

Если же колода карт содержит еще и джокер, то A и В станут зависимыми, так как 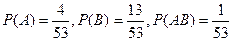и

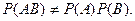
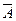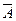Нетрудно видеть (проверьте самостоятельно), что если события A и В независимы, то независимы будут также события и В, и .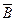

Понятие независимости двух событий распространяется на случай нескольких событий.

Определение 5. События A _{1, A 2}…, A _n называются независимыми, если вероятность любого из них А_i не меняется при наступлении какого угодно числа событий A _j , 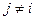из той же совокупности.

Нетрудно видеть (используя определение 4), что это определение может быть сформулировано по-другому.

Определение 6. События A _{1, A 2}…,А_n , называются независимыми, если для любого подмножества 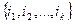множества 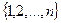выполняются равенства

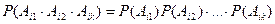. (7)

Можно также, показать, что из независимости событий A _{1, A 2}…,А_n вытекает, что любое из этих событий независимо от любой комбинации остальных.

Еще раз подчеркнём, что в большинстве случаев, основанием для вывода о независимости служат интуитивные соображения. Так, например, если бросают подряд две монеты, то ясно, что выпадение той или иной стороны на одной монете не оказывает никакого влияния на условия бросания другой, и, значит, следующие два события: выпадение герба на одной монете (событие A) и выпадение герба (или решки) на другой (событие В) – являются независимыми.

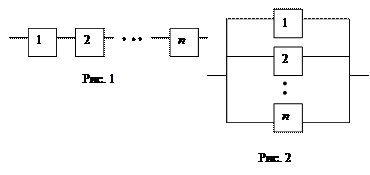
Пример 4. Электрическая схема состоит из n последовательно соединённых блоков (рис 1). Надёжность (т.е. вероятность безотказной работы) каждого блока равна соответственно р₁, р₂, …, р_n. Считая выходы из строя различных блоков независимыми событиями, найти надёжность всей схемы в целом.

Решение (см. §4). Событие, заключающееся в исправной работе i-го блока, обозначим A_i; исправность схемы в целом обозначим через событие А.

Так как блоки соединены последовательно , то событие А имеет место в том и только в том случае, когда имеют место все A_i.

Поэтому 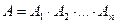, откуда в силу независимости событий 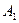, 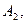…,А_n следует

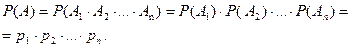
Та же самая задача для схемы из параллельно соединенных блоков (рис 2) приводит к другому ответу. В этом случае 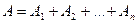и значит

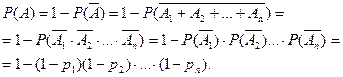
Замечание. На практике формулу умножения полезно применять вместе с формулой сложения. При этом событие А, вероятность которого требуется найти, стараются представить в виде суммы нескольких попарно несовместных слагаемых: 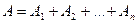, а каждое из слагаемых А_к ,в свою очередь, представить в виде произведения нескольких независимых событий.

Пример 5. Имеются две урны. В первой находится 1 белый шар, 3 чёрных и 4 красных, во второй – 3 белых, 2 чёрных и 3 красных. Из каждой урны наугад извлекают по одному шару, после чего сравнивают их цвета. Найти вероятность того, что цвета вытащенных шаров совпадают (событие А).

Решение. Обозначим событие, состоящее в извлечении из первой урны белого шара, через В₁, чёрного – С₁, красного – D₁. Аналогичные события для второй урны обозначим В₂, С₂, D₂. Событие А распадается на три (несовместных) варианта: В₁В₂, С₁С₂, D₁D₂.

Тогда, применяя формулу сложения (для несовместных событий) и формулу умножения (для независимых событий)), получим