Производная сложной функции
Тема 2.3 Производная функции (повторение).
Основные понятия
Определение производной
Пусть в некоторой окрестности точки 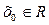 определена функция
определена функция 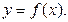 Производной функции fв точке
Производной функции fв точке 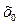 называется предел, если он существует,
называется предел, если он существует,
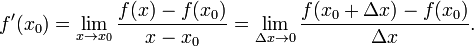
Общепринятые обозначения производной функции
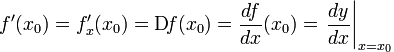
Правила дифференцирования
Операция нахождения производной называется дифференцированием. При выполнении этой операции часто приходится работать с частными, суммами, произведениями функций, а также с «функциями функций», то есть сложными функциями. Исходя из определения производной, можно вывести правила дифференцирования, облегчающие эту работу.
Если C — постоянное число и 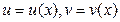 — некоторые дифференцируемые функции, то справедливы следующие правила дифференцирования:
— некоторые дифференцируемые функции, то справедливы следующие правила дифференцирования:
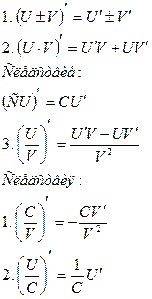
Производная сложной функции
Сложная функция (композиция функций) записывается в виде
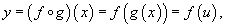
где u = g(x) - внутренняя функция, являющаяся, в свою очередь, аргументом (если функций больше, то промежуточным аргументом) для внешней функции f. Если f и g - дифференцируемые функции, то сложная функция также дифференцируема по x и ее производная равна
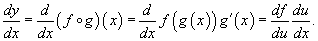
Данная формула показывает, что производная сложной функции равна произведению производной внешней функции на производную от внутренней функции. Важно, однако, что производная внутренней функции вычисляется в точке x, а производная внешней функции - в точке u = g(x)! Эта формула легко обобщается на случай, когда сложная функция состоит из нескольких "слоев", вложенных иерархически друг в друга.
Таблица производных функций независимой переменной.
| Функция | Производная | Функция | Производная | |
Постоянная 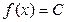 | 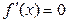 | Тригонометрические 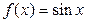 | 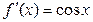 | |
Степенная 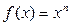 | 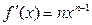 | |||
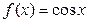 | 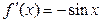 | |||
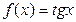 | 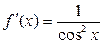 | |||
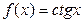 | 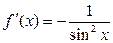 | |||
Логарифмическая 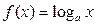 В частности В частности 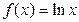 | 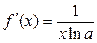 | Обратные тригонометрические 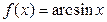 | 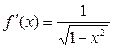 | |
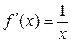 | ||||
Показательная 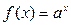 В частности В частности 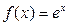 | 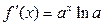 | |||
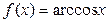 | 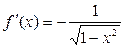 | |||
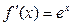 | 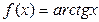 | 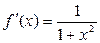 | ||
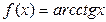 | 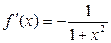 |
Таблица производных функций, аргументом которой является функция.
