Детерминированных сигналов

Литература: [Л.1], с 77-83

[Л.2], с 22-26

[Л.3], с 39-43

Во многих радиотехнических задачах часто возникает необходимость сравнения сигнала и его копии, сдвинутой на некоторое время 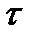. В частности такая ситуация имеет место в радиолокации, где отраженный от цели импульс поступает на вход приемника с задержкой во времени. Сравнение этих сигналов между собой, т.е. установление их взаимосвязи, при обработке позволяет определять параметры движения цели.

Для количественной оценки взаимосвязи сигнала и его сдвинутой во времени копии вводится характеристика

, (2.57)

Которая называется автокорреляционной функцией (АКФ).

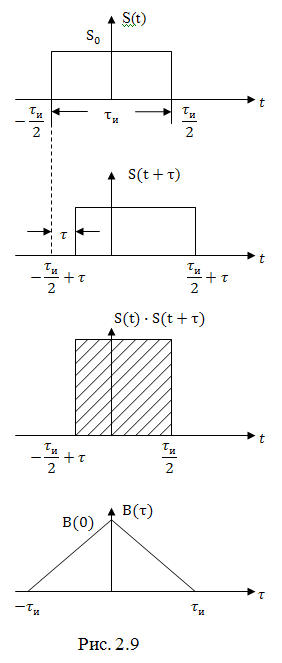
Для пояснения физического смысла АКФ приведем пример, где в качестве сигнала выступает прямоугольный импульс длительностью 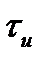и амплитудой . На рис. 2.9 изображены импульс, его копия, сдвинутая на интервал времени 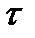и произведение 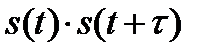. Очевидно, интегрирование произведения дает значение площади импульса, являющегося произведением . Это значение при фиксированном 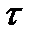можно изобразить точкой в координатах 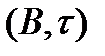. При изменении 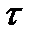мы получим график 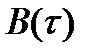автокорреляционной функции.

Найдем аналитическое выражение 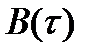. Так как

то подставляя это выражение в (2.57), получим

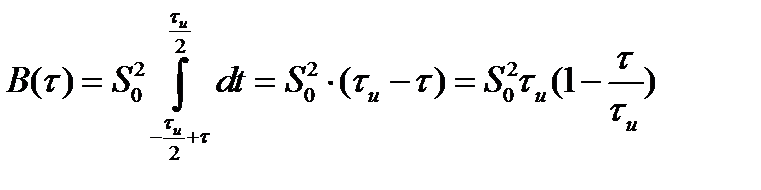. (2.58)

Если осуществлять сдвижку сигнала влево, то аналогичными вычислениями нетрудно показать, что

. (2.59)

Тогда объединяя (2.58) и (2.59), получим

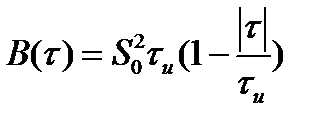. (2.60)

Из рассмотренного примера можно сделать следующие важные выводы, распространяющиеся на сигналы произвольной формы:

1. Автокорреляционная функция непериодического сигнала с ростом 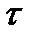убывает (необязательно монотонно для других видов сигналов). Очевидно, при 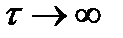АКФ также стремиться к нулю.

2. Своего максимального значения АКФ достигает при 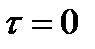. При этом, 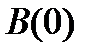равна энергии сигнала. Таким образом, АКФ является энергетической характеристикой сигнала. Как и следовало ожидать при 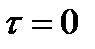сигнал и его копия полностью коррелированны (взаимосвязаны).

3. Из сравнения (2.58) и (2.59) следует, что АКФ является четной функцией аргумента 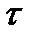, т.е.

.

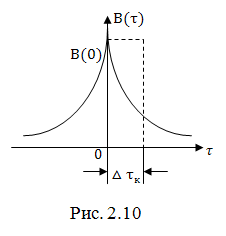
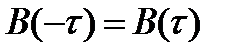Важной характеристикой сигнала является интервал корреляции. Под интервалом корреляции понимают интервал времени 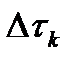, при сдвижке на который сигнал 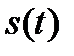и его копия 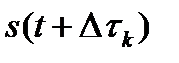становятся некоррелированными.

Математически интервал корреляции определяется следующим выражением

,

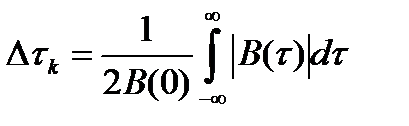или поскольку 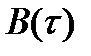– четная функция

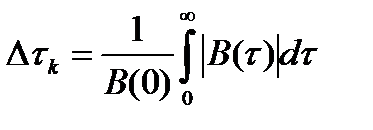. (2.61)

На рис. 2.10 изображена АКФ сигнала произвольной формы. Если построить прямоугольник, по площади равный площади под кривой 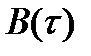при положительных значениях 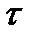(правая ветвь кривой), одна сторона которого равна 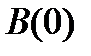, то вторая сторона будет соответствовать .

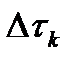Найдем интервал корреляции для прямоугольного импульса. Подставляя (2.58) в (2.60) после несложных преобразований, получим:

,

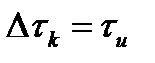что и следует из рис. 2.9.

По аналогии с автокорреляционной функцией степень взаимосвязи двух сигналов 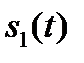и оценивается взаимной корреляционной функцией (ВКФ)

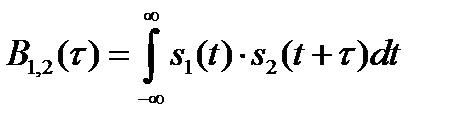. (2.62)

Найдем взаимную корреляционную функцию двух сигналов: прямоугольного импульса с амплитудой 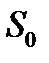и длительностью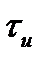

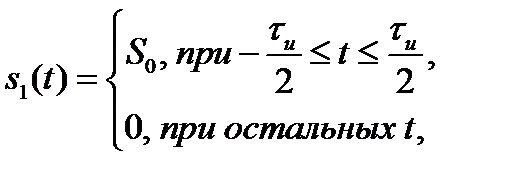
и треугольного импульса той же амплитуды и длительности

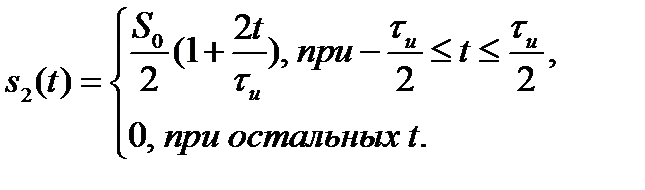
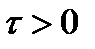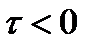Воспользовавшись (2.61) и вычисляя интегралы отдельно для и , получим:

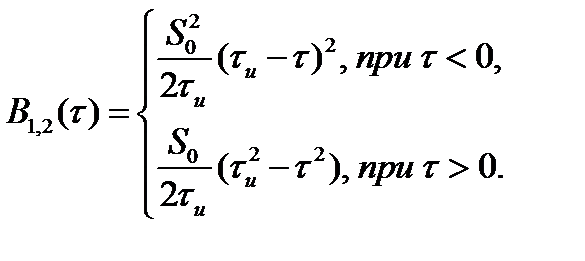
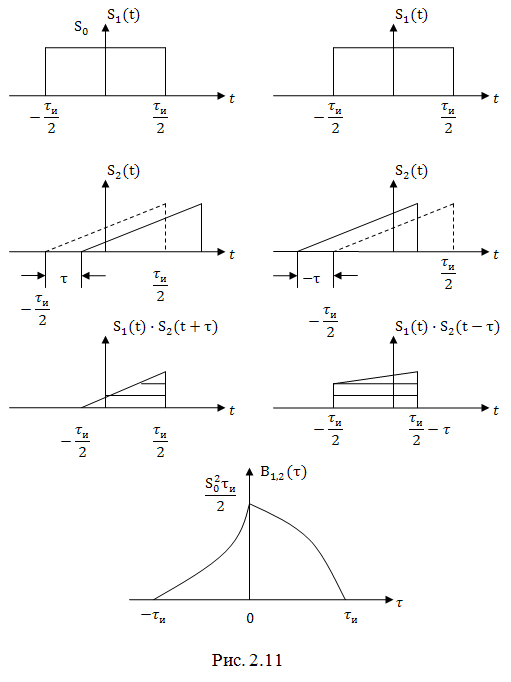
Графические построения, иллюстрирующие вычисления ВКФ, приведены на рис. 2.11

Здесь пунктирными линиями показано исходное (при 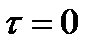) положение треугольного импульса.

При 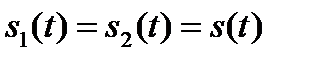выражение (2.61) преобразуется в (2.57). Отсюда следует, что АКФ является частным случаем ВКФ при полностью совпадающих сигналах.

Отметим основные свойства ВКФ.

1. Так же, как и автокорреляционная функция, ВКФ является убывающей функцией аргумента 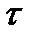. При 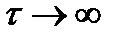ВКФ стремиться к нулю.

2. Значения взаимной корреляционной функции при произвольных 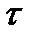представляют собой значения взаимной энергии (энергии взаимодействия) сигналов 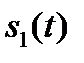и .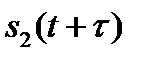

3. При 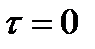взаимная корреляционная функция (в отличие от автокорреляционной) не всегда достигает максимума.

4. Если сигналы 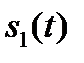и 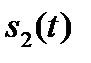описываются четными функциями времени, то ВКФ тоже четна. Если же хотя бы один из сигналов описывается нечетной функцией, то ВКФ так же нечетна. Первое утверждение легко доказать, если вычислить ВКФ двух прямоугольных импульсов противоположной полярност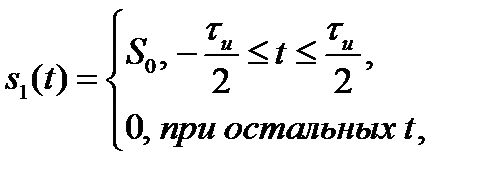и

и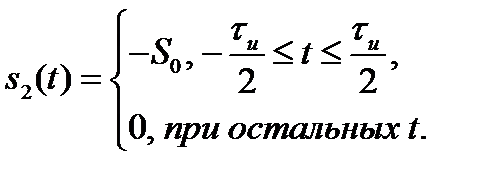

Взаимная корреляционная функция таких сигналов

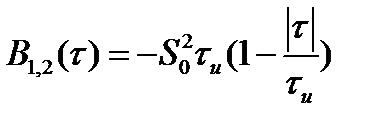, (2.63)

является четной функцией аргумента .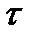

Что же касается второго утверждения рассмотренный пример вычисления ВКФ прямоугольного и треугольного импульсов доказывает его.

В некоторых прикладных задачах радиотехники используют нормированную АКФ

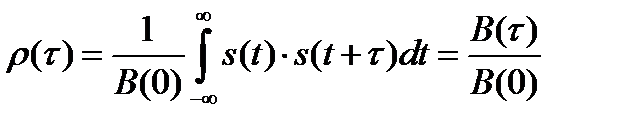, (2.64)

и нормированную ВКФ

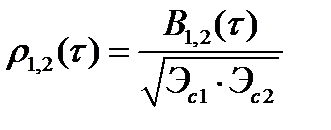, (2.65)

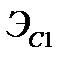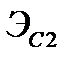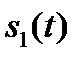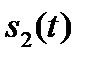где и – собственные энергии сигналов и . При 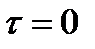значение нормированной ВКФ 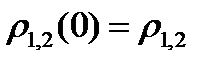называют коэффициентом взаимной корреляции. Если 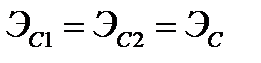, то коэффициент взаимной корреляции

.

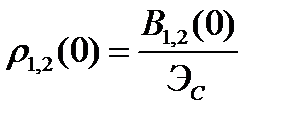Очевидно, значения 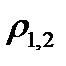лежат в пределах от -1 до +1. Если сравнить (2.65) с (1.32), то можно убедиться, что коэффициент взаимной корреляции соответствует значению косинуса угла между векторам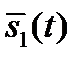и и 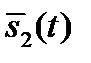при геометрическом представлении сигналов.

Рассчитаем коэффициент взаимной корреляции для рассмотренных выше примеров. Так как энергия сигнала прямоугольного импульса составляет

,

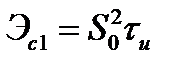а треугольного импульса

,

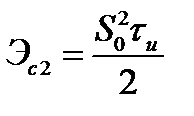то коэффициент взаимной корреляции в соответствии с (2.62) и (2.65) будет равен 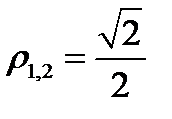. Что же касается второго примера, то для двух прямоугольных импульсов одинаковой амплитуды и длительности, но противоположной полярности, .

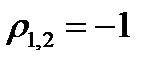Экспериментально АКФ и ВКФ могут быть получены с помощью устройства, структурная схема которого изображена на рис. 2.12

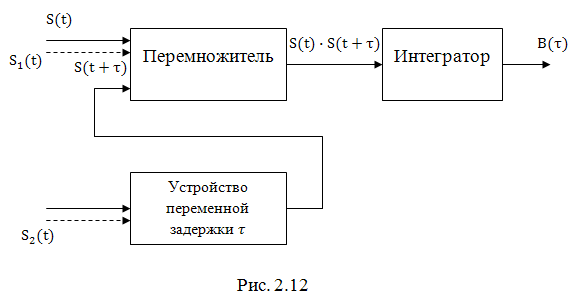
При снятии АКФ на один из входов перемножителя поступает сигнал 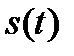, а на второй – этот же сигнал, но задержанный на время 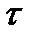. Сигнал, пропорциональный произведению 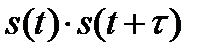, подвергается операции интегрирования. На выходе интегратора формируется напряжение, пропорциональное значению АКФ при фиксированном 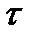. Изменяя время задержки, можно построить АКФ сигнала.

Для экспериментального построения ВКФ сигнал 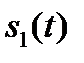подается на один из входов перемножителя, а сигнал 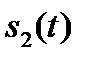– на устройство задержки (входящие цепи показаны пунктиром). В остальном, устройство работает аналогичным образом. Отметим, что описанное устройство называется коррелятором и широко используется в различных радиотехнических системах для приема и обработки сигналов.

До сих пор мы проводили корреляционный анализ непериодических сигналов, обладающих конечной энергией. Вместе с тем, необходимость подобного анализа часто возникает и для периодических сигналов, которые теоретически обладают бесконечной энергией, но конечной средней мощностью. В этом случае АКФ и ВКФ вычисляются усреднением по периоду и имеют смысл средней мощности (собственной или взаимной соответственно). Таким образом, АКФ периодического сигнала:

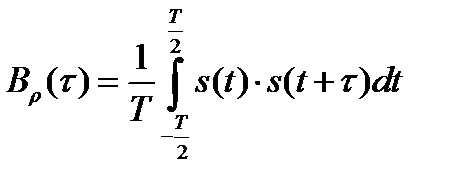, (2.66)

а взаимная корреляционная функция двух периодических сигналов с кратными периодами:

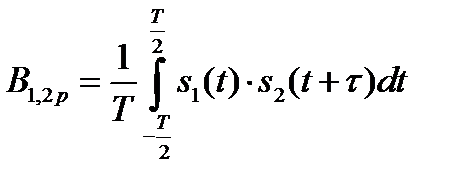, (2.67)

где 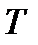– наибольшее значение периода.

Найдем автокорреляционную функцию гармонического сигнала

,

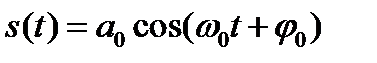где 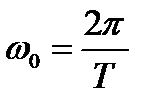– круговая частота, 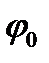– начальная фаза.

Подставляя это выражение в (2.66) и вычисляя интеграл с использованием известного тригонометрического соотношения:

,

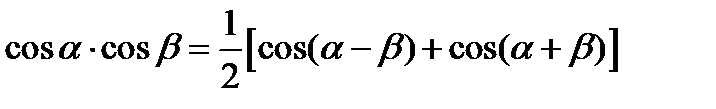получим:

.

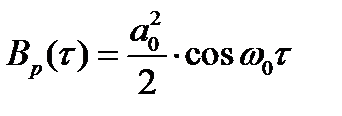Из рассмотренного примера можно сделать следующие выводы, справедливые для любого периодического сигнала.

1. АКФ периодического сигнала является периодической функцией с тем же периодом.

2. АКФ периодического сигнала является четной функцией аргумента .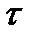

3. При 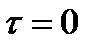значение 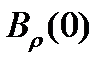представляет собой среднюю мощность, которая выделяется на сопротивлении в 1 Ом и имеет размеренность .

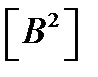4. АКФ периодического сигнала не содержит информации о начальной фазе сигнала.

Следует также отметить, что интервал корреляции периодического сигнала .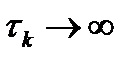

А теперь вычислим взаимную корреляционную функцию двух гармонических сигналов одинаковой частоты, но отличающихся амплитудами и начальными фазами

и .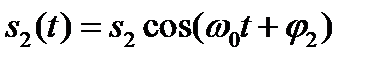

Воспользовавшись (2.67) и проводя несложные вычисления, получим

,

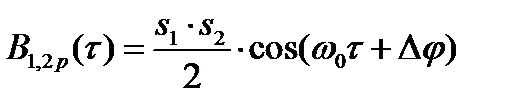где 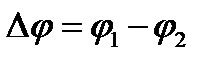– разность начальных фаз сигналов 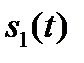и .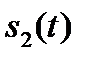

Таким образом, взаимная корреляционная функция двух рассматриваемых сигналов содержит информацию о разности начальных фаз. Это важное свойство широко используется при построении различных радиотехнических устройств, в частности, устройств синхронизации некоторых систем радиоавтоматики и других.

В заключение установим связь между АКФ непериодического сигнала и его энергетическим спектром, определение которого [см. (2.51)] было дано выше. Для этого воспользуемся (2.49) при 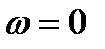. Тогда получим соотношение

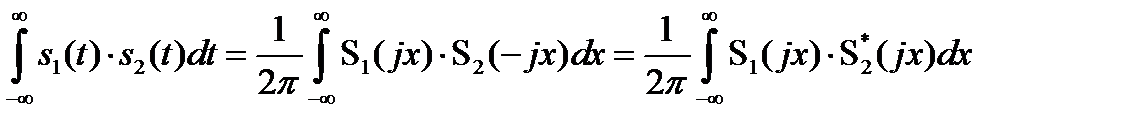, (2.68)

где – функция, комплексно сопряженная с .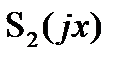

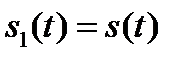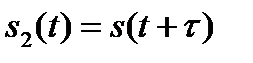Положим теперь и . В соответствии с (2.45) преобразование Фурье имеет вид

.

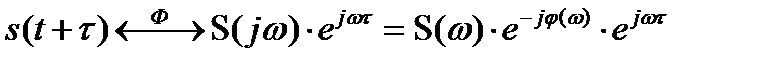С другой стороны

.

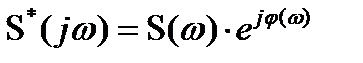Подставляя эти выражения в (2.68), получим

.

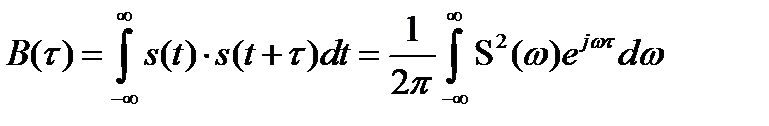Но 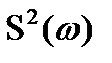в соответствие с (2.51) есть энергетический спектр. Тогда окончательно

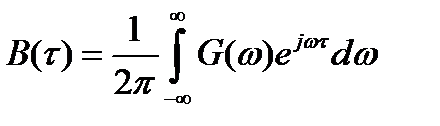. (2.69)

Применяя к 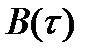прямое преобразование Фурье, приходим к соотношению

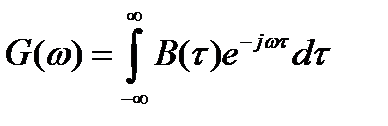. (2.70)

Таким образом, АКФ и энергетический спектр сигнала связаны парой преобразований Фурье.

Так как 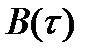и 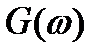– вещественные и четные функции, выражения (2.69) и (2.70) можно записать соответственно в виде

, (2.71)

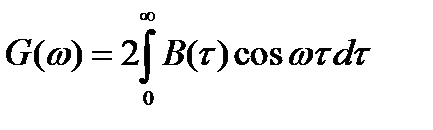. (2.72)

Рассмотренный корреляционно-спектральный анализ позволяет дать еще одну трактовку эффективной ширины спектра. Если известен энергетический спектр, то эффективная ширина спектра определяется так:

. (2.73)

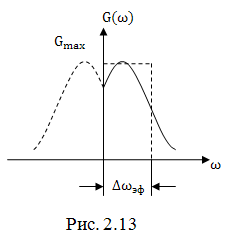
Иными словами 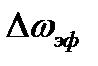представляет собой сторону прямоугольника по площади равного площади под кривой одностороннего спектра, вторая сторона которого равна 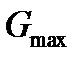(рис.2.13). Очевидно, произведение эффективной ширины энергетического спектра 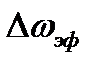на величину интервала корреляции 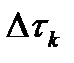есть величина постоянная

.

Таким образом, и в этом случае мы сталкиваемся с проявлением принципа неопределенности: чем больше интервал корреляции, тем меньше ширина энергетического спектра, и наоборот.

Контрольные вопросы к главе 2

1. Что такое система базисных тригонометрических функций?

2. Как можно записать тригонометрический ряд Фурье?

3. Дайте определение амплитудного и фазового спектра периодического сигнала.

4. Какой характер носит спектр последовательности прямоугольных импульсов?

5. Чем отличается спектр одиночного импульса от спектра периодической последовательности импульсов?

6. Запишите прямое и обратное преобразование Фурье.

7. Как найти эффективную длительность и эффективную ширину спектра прямоугольного сигнала?

8. Что представляет собой спектр сигнала в виде дельта-функции?

9. Дайте определение автокорреляционной функции детерминированного сигнала.

10. Что такое взаимная корреляционная функция двух сигналов?

11. Как найти коэффициент взаимной корреляции?

12. Какими свойствами обладает автокорреляционная функция периодического сигнала?