ЛЕКЦИЯ № 2. НЕОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ
Вопрос 2.1. Замена переменных в неопределенном интеграле.
В подавляющем большинстве случаев сведение неопределенного интеграла к табличному или сумме табличных интегралов возможно только при использовании замены переменных. Справедлива следующая теорема
Теорема 2.1. Пусть дан неопределенный интеграл  и дифференцируемая функция
и дифференцируемая функция  , тогда справедливо равенство
, тогда справедливо равенство
 ,
,
если существует неопределенный интеграл в правой части.
Доказательство. Два неопределенных интеграла равны, если равны производные от них:
 .
.
Тогда вычисляя производные от интегралов
 ,
,
 .
.
убеждаемся в равенстве производных, а следовательно и в равенстве самих производных.
Конец доказательства.
Замечание 2.1. Если формулу применять слева на право, то метод называют методом замены переменных.
Замечание 2.2. Если формулу применять справа налево, то метод называют методом подведения множителя под знак дифференциала.
Пример 2.1.  .
.
Конец примера.
Пример 2.2.
 .
.
Конец примера.
Пример 2.3.
 .
.
Конец примера.
Пример 2.4.

Конец примера.
Вопрос 2.2. Метод интегрирования по частям.
Теорема 2.2. Пусть  ,
,  дифференцируемые функции и существует интеграл, тогда справедливо формула интегрирования по частям:
дифференцируемые функции и существует интеграл, тогда справедливо формула интегрирования по частям:

или

Доказательство. Из формулы дифференцирования по частям

найдем
 .
.
Интегрируя последнее равенство, получим
 ,
,
где учтено, что  .
.
Так как  и
и  , то формулу интегрирования по частям можно представить в виде
, то формулу интегрирования по частям можно представить в виде
 .
.
Конец доказательства.
Замечание 2.3. При применении метода подстановки и метода интегрирования по частям полезны выражения:
 ,
,
 ,
,
 ,
,
 ,
,
 .
.
Пример 2.5. Интегралы вида  , где
, где 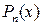 ‑ многочлен n-й степени.
‑ многочлен n-й степени.

Конец примера.
Пример 2.6. Интегралы вида  .
.

Конец примера.
Пример 2.7. Интегралы вида  .
.
Эти интегралы называются возвратными. Вычисляя их дважды по частям, получим уравнение, из которого можно найти значение интеграла.

Решая это уравнение, найдем
 .
.
Конец примера.
ЛЕКЦИЯ №3 НЕОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ.
Вопрос 3.1. Рациональные дроби.
Определение 3.1. Рациональной дробью называется функция вида  , где
, где 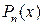 и
и  ‑ многочлены степени n и m. Если n<m, то дробь называется правильной, в противном случае дробь называется неправильной.
‑ многочлены степени n и m. Если n<m, то дробь называется правильной, в противном случае дробь называется неправильной.
Конец определения.
Пример 3.1.
 ‑ правильная рациональная дробь,
‑ правильная рациональная дробь,
 ‑ неправильная рациональная дробь,
‑ неправильная рациональная дробь,
 ‑ неправильная рациональная дробь.
‑ неправильная рациональная дробь.
Конец примера.
Теорема 3.1. Всякую неправильную рациональную дробь можно представить в виде суммы многочлена и правильной рациональной дроби:
 ,
,
где  ‑ многочлены (последний из них называется остатком от деления многочлена
‑ многочлены (последний из них называется остатком от деления многочлена 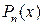 на многочлен
на многочлен  ).
).
Пример 3.2. Деление многочлена на многочлен уголком

Следовательно, можно записать
 .
.
Конец примера.
