Изображения цилиндра и конуса

1. Изображение цилиндра. Пусть цилиндр-оригинал F₀ установлен на горизонтальной плоскости. Тогда для того, чтобы изображение было наглядным, плоскость изображения p выберем вертикальной. При этом ось цилиндра и его образующие будут параллельны плоскости p. Далее, снова из соображений наглядности, направление проектирования выберем параллельным плоскости, проходящей через ось цилиндра перпендикулярно к плоскости p. Если проектирование будет ортогональным (параллельным основаниям цилиндра), то цилиндр-оригинал спроектируется в прямоугольник (рис. 52). Такое изображение также не будет наглядным. Поэтому направление проектирования не должно быть параллельным основаниям (рис. 53).

Рассмотрим, как изображается цилиндр F₀ при выбранном нами способе проектирования. Пусть w₀ – окружность верхнего основания цилиндра F₀, А₀В₀ – ее диаметр, параллельный плоскости изображения p, а С₀D₀ – перпендикулярный ему диаметр. При проектировании на плоскость p окружность w₀ спроектируется в эллипс g с осями АВ и СD, которые являются проекциями диаметров А₀В₀ и С₀D₀. При этом вновь из соображений наглядности будем считать, что направление проектирования выбрано таким образом, что CD < AB.

Так как диаметр С₀D₀ лежит в плоскости, проходящей через ось цилиндра, перпендикулярно плоскости p, то проекции D, O, C, О' точек D₀, O₀, C₀, соответственно, принадлежат одному вертикальному отрезку. Касательная к окружности w₀ в точке А₀ лежит в плоскости верхнего основания и параллельна диаметру С₀D₀, поэтому она спроектируется в касательную к эллипсу g в точке А, и, значит, параллельна CD (рис. 54). Пусть 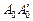– образующая цилиндра. Плоскость, в которой лежат рассмотренная выше касательная и прямая 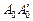, перпендикулярна плоскости p, поэтому проекции этих прямых совпадают. Таким образом, проекция АА¢ образующей 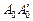лежит на касательной к эллипсу g в точке А. Аналогично, проекция ВВ¢ образующей лежит на касательной к эллипсу g в точке В.

Нижнее основание цилиндра проектируется в эллипс g¢, равный эллипсу g. При этом эллипс g¢ будет образом эллипса g при параллельном переносе на вектор .

Задача 1. Построить изображение правильной четырехугольной призмы, вписанной в цилиндр.

Решение. Основаниями правильной четырехугольной призмы являются квадраты, вписанные в окружности оснований цилиндра. Так как диагонали квадрата перпендикулярны, то их изображением будут сопряженные диаметры эллипса, изображающего окружность основания.

Строим эллипс – изображение окружности основания. Затем выполняем построение изображений квадратов, вписанных в основания цилиндра, и изображение боковых ребер призмы (рис. 55). На левом рисунке для изображения квадратов используются оси эллипсов. Такое изображение недостаточно наглядно, так как изображения двух противоположных ребер призмы лежат на одной прямой. Более наглядное изображение дано на правом рисунке. Здесь для построения квадратов используются сопряженные диаметры эллипсов, не являющиеся осями.

2. Изображение конуса. Пусть вновь конус-оригинал F₀ установлен на горизонтальной плоскости. Из соображений наглядности выберем плоскость изображения p вертикальной. Тогда ось S₀O₀ конуса будет параллельна плоскости p. Направление проектирования возьмем параллельным плоскости, проходящей через ось конуса перпендикулярно плоскости изображения p. При этом будем дополнительно требовать, чтобы прямая этого направления, проходящая через вершину S₀ конуса, пересекала плоскость основания вне окружности основания в точке (рис. 56).

Пусть А₀В₀, C₀D₀ – взаимно перпендикулярные диаметры окружности w₀ основания конуса, при этом А₀В₀║p. Тогда . Проведем в плоскости основания касательные , к окружности w₀. Ясно, что M₀N₀║А₀В₀.

Рассмотрим плоскости , . Эти плоскости содержат образующие S₀M₀, S₀N₀ конуса и параллельны направлению проектирования. При проектировании конуса на плоскость p окружность w₀ проектируется в эллипс g, диаметры A₀B₀, C₀D₀ окружности – в оси AB, CD эллипса. Вершина S₀ конуса в точку S, лежащую на прямой CD вне эллипса (рис. 57). Так как плоскость параллельна направлению проектирования, то прямые и S₀M₀ проектируются в одну и ту же прямую. Но – касательная к окружности w₀ в точке М₀, поэтому ее проекцией будет касательная к эллипсу g в точке М, где М – проекция точки М₀. Таким образом, проекцией образующей S₀M₀ конуса будет отрезок SM касательной к эллипсу g в точке М, проведенной из точки S. Аналогично строится изображение SN образующей S₀N₀.

Задача 2. Построить изображение конуса, вписанного в правильную четырехугольную пирамиду.

Решение. Построение заданной комбинации фигур удобно начать с построения изображения квадрата, описанного около окружности. Окружность изображается эллипсом, а стороны параллелограмма, изображающего квадрат, касаются эллипса в концах его сопряженных диаметров. На левом рисунке (рис. 58) в качестве сопряженных диаметров взяты его оси, а на правом – сопряженные диаметры осями не являются.

Далее, вертикальным отрезком SO изображается ось конуса, строятся касательные к эллипсу, проведенные из точки S, и изображения боковых ребер пирамиды.