Модульна контрольна робота № 1
Висловлення і предикати. Множини, відповідності, відношення
І – варіант
1. Дано множини А і В. А={1, 2, 3, 4, 5}, В={3, 4, 5, 6, 7}.
Знайти: А 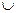 В, А∩В, А\В, В\A.
В, А∩В, А\В, В\A.
2. Зобразити декартів добуток множин А і В на координатній площині, якщо:
А={х | х Є Z, -3 ≤ х ≤ 3}, В={у | у Є R, -1 ≤ у ≤ 2}.
3. Встановити, в якому відношенні перебувають поняття А: «трикутник»,
В: «рівнобедрений трикутник». Зобразити це відношення за допомогою кругів Ейлера.
4. Дано множину А, А={1, 2, 3, 4, 5, 6} і відношення: «х більше у на 2». Визначити властивості даного відношення на даній множині. Побудувати граф цього відношення.
5. Відомо, що висловлення А – істинне, В – хибне, С – істинне. Визначте, які з висловлень істинні, а які хибні. Обґрунтуйте відповідь, використовуючи означення логічних операції над висловленнями, таблиці істинності висловлень: а) А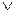 В
В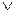 С; б) А
С; б) А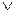 (В
(В 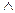 С).
С).
ІІ – варіант
1. Дано множини А і В. А={ 3, 4, 5, 6, 7}, В={6, 7, 8, 9, 10}.
Знайти: А 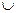 В, А∩В, А\В, В\A.
В, А∩В, А\В, В\A.
2. Зобразити декартів добуток множин А і В на координатній площині, якщо:
А={х | х Є R, -1 ≤ х ≤ 3}, В={у | у Є Z, -2 ≤ у ≤ 2}.
3. Встановити в якому відношенні перебувають поняття:
А «рівносторонній трикутник», В «рівнобедрений трикутник».
Зобразити це відношення за допомогою кругів Ейлера.
4. Дано множину А, А={ 2, 4, 6, 8, 10} і відношення «х в два рази більше за у».
Визначити властивості даного відношення на даній множині. Побудувати граф цього відношення.
5. Відомо, що висловлення А – істинне, В – хибне, С – істинне. Визначте, які з висловлень істинні, а які хибні. Обґрунтуйте відповідь, використовуючи означення логічних операції над висловленнями, таблиці істинності висловлень: а) А 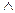 (В
(В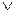 С); б) А
С); б) А 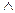 В
В 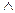 С.
С.
Варіант 3
1. Дано множини А і В. А={4, 5, 6, 7}, В = {3, 4, 5, 6, 7, 8}.
Знайти: А 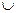 В, А∩В, А\В, В\A.
В, А∩В, А\В, В\A.
2. Зобразити декартів добуток множин А і В на координатній площині, якщо:
А={1, 2, 3}, В={2, 3, 4, 5, 6}.
3. Встановити, в якому відношенні перебувають поняття А: «паралелограм», В: «ромб». Зобразити це відношення за допомогою кругів Ейлера.
4. Елементи множини Х = {0, 1, 3, 4, 6} знаходяться у відношенні Р = {(0, 1), (0, 3), (0, 4), (0, 6), (1, 4), (6, 6)}. Побудуйте граф цього відношення.
5. Відомо, що висловлення А – хибне, В – істинне, С – хибне . Визначте, які з висловлень істинні, а які хибні. Обґрунтуйте відповідь, використовуючи означення логічних операції над висловленнями, таблиці істинності висловлень: а) А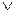 В
В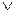 С; б) А
С; б) А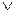 (В
(В 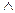 С).
С).
Варіант 4
1. Дано множини А і В. А={1, 2, 3}, В={3, 4, 5, 6, 7}.
Знайти: А 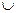 В, А∩В, А\В, В\A.
В, А∩В, А\В, В\A.
2. Зобразити декартів добуток множин А і В на координатній площині, якщо:
А={х | х Є Z, -3 ≤ х ≤ 3}, В={2, 3, 4, 5}.
3. Встановити, в якому відношенні перебувають поняття А: «прямокутник»,
В: «паралелограм». Зобразити це відношення за допомогою кругів Ейлера.
4. Побудуйте граф відношення «більше або дорівнює», заданого на множині {0, 1, 2, 3, 4}. Як задати це відношення за допомогою нерівності з двома змінними?
5. Відомо, що висловлення А – хибне, В – істинне, С – істинне. Визначте, які з висловлень істинні, а які хибні. Обґрунтуйте відповідь, використовуючи означення логічних операції над висловленнями, таблиці істинності висловлень: а) А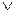 В
В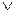 С; б) А
С; б) А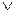 (В
(В 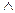 С).
С).
