Основные теоремы о пределах

Пусть f(x) и j (x) – функции, для которых существуют пределы при х ® х₀ (¥):

,

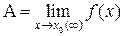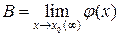
Тогда имеют место следующие теоремы о пределах:

1. Функция не может иметь более одного предела.

2. Предел алгебраической суммы конечного числа функций равен такой же сумме пределов этих функций:

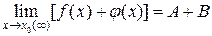
3. Предел произведения конечного числа функций равен произведению пределов этих функций:

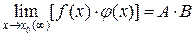
В частности, постоянный множитель можно выносить за знак предела:

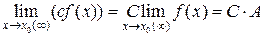
4. Предел частного двух функций равен частному пределов этих функций (при условии, что предел делителя не равен нулю):

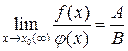(B ¹ 0)

Пример.Вычислить предел .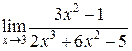

◄ Пределы числителя и знаменателя существуют и предел знаменателя не равен нулю. Пользуясь теоремой о пределе частного, получаем:

. ►

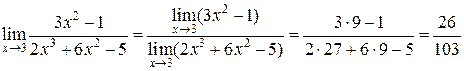Пример. Вычислить .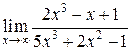

◄ Теорему о переделе частного здесь применять нельзя, т.к. числитель и знаменатель конечного предела не имеют. Имеем неопределенность 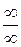. В подобных случаях для раскрытия неопределенности целесообразно числитель и знаменатель разделить на степень х с наивысшим показателем, а затем перейти к пределу:

. ►

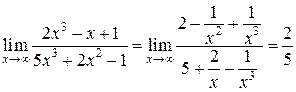Замечательные пределы

Первый замечательный предел:

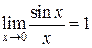
Второй замечательный предел:

,

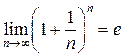где 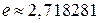–число Эйлера, которое является основанием для натуральных логарифмов. Последний предел можно записать в других формах:

,

.

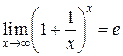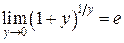Пример. Вычислить .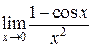

◄ Для раскрытия подобных неопределенностей 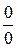используется первый замечательный предел:

.►

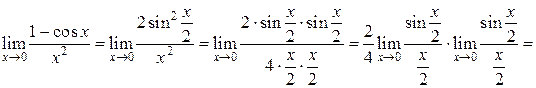
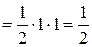Непрерывность функции.

Функция f(x) называется непрерывной в точке х₀, если она удовлетворяет следующим условиям:

1) она определена в точке 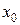,т.е. существует f(х₀);

2) она имеет конечный предел функции при х ® х₀;

3) этот предел равен значению функции в точке х₀,

т.е.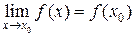

Например, в точке х = 0 функция 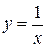не является непрерывной (нарушено 1-е условие).

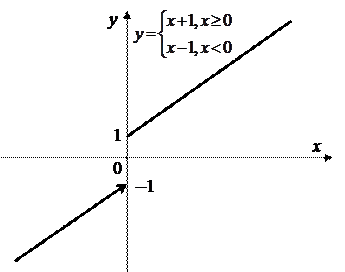Функция, заданная выражением:

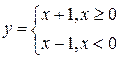
в точке х = 0 не является непрерывной из-за отсутствия предела при х ® 0, хотя существуют пределы слева и справа (см. рис.).

Точка 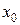называется точкой разрыва функции 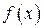, если эта функция в данной точке не является непрерывной. Существует две разновидности точек разрыва.

Точка разрыва 1-го рода: существуют конечные односторонние пределы функции слева и справа при х ® х₀, не равные друг другу.

В качестве примера можно указать точку х = 0 для рассмотренной выше функции .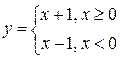

Точка разрыва 2-го рода: хотя бы один из односторонних пределов равен бесконечности или не существует.

В качестве примера можно указать точку х = 0 для функции .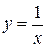

Свойства функций непрерывных в точке:

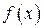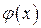1. Если функции и непрерывны в точке 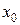, то их сумма 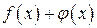, произведение 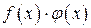и частные 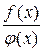( 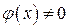) являются функциями, непрерывными в точке .

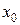2. Если функция y = f(x) непрерывна в точке х₀ и f(x₀) > 0, то существует такая окрестность точки x₀, в которой и f(x) > 0.

3. Если функция y = f(u) непрерывна в точке u₀ и f(x₀) > 0, а функция 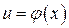непрерывна в точке х₀, то сложная функция y = f[j(х)] непрерывна в точке х₀.

Функция y = f(x) называется непрерывной на промежутке Х, если она непрерывна в каждой точке этого промежутка.

Свойства функций непрерывных на отрезке:

1. Если функция y = f(x) непрерывна на отрезке [a, b], то она ограничена на этом отрезке.

2. Если функция y = f(x) непрерывна на отрезке [a, b], она достигает на этом отрезке наименьшего значения m и наибольшего значения M.

3. Если функция y = f(x) непрерывна на отрезке [a, b] и ее значения на концах отрезка f(a) и f(b) имеют противоположные знаки, то внутри отрезка найдется точка x Î (a, b) такая, что f(x)=0.

Лекция 2.7.2 «Производная. Дифференциал»

Учебные вопросы:

1. Производная

2. Дифференциал

Производная

Производной от функции называется предел отношения приращения функции к приращению независимой переменной при стремлении последнего к нулю (если этот предел существует):

.

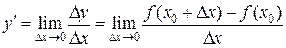Другие обозначения производной: .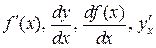

Дифференцирование функции – это нахождение производной этой функции. Если функция имеет в точке x производную (конечную), то она называется дифференцируемой в этой точке.

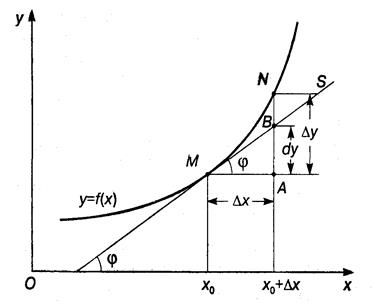Геометрический смысл производной: производная 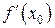равна тангенсу угла между осью Ox и касательной, проведенной к графику функции в точке 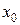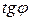(см. рис.).

Механический смысл: производная пути по времени 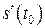есть скорость точки в момент 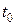т.е. .

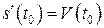Производительность труда в момент 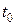есть производная объема произведенной продукции по времени .

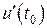Теорема. Если функция дифференцируема в точке 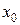, то она в этой точке непрерывна.

Обратная теорема, вообще говоря, не верна, т.е. непрерывная функция может быть не дифференцируемой в точке 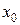, например, функция 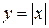в точке .

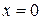Правила дифференцирования

1. Производная константы равна нулю, т.е. 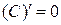, где С - const.

2. Производная аргумента равна 1, т.е. .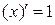

3. Производная алгебраической суммы конечного числа дифференцируемых функций равна такой же сумме производных этих функций, т.е.

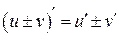
4. Производная произведения двух дифференцируемых функций:

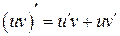
Следствие. Постоянный множитель можно выносить за знак производной: 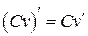, где С - const.

5. Производная частного двух дифференцируемых функций:

.

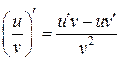при условии, что .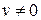

6. Производная сложной функции 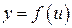, где 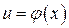, где y и u – дифференцируемые функции своих аргументов, равна

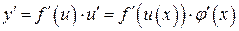
Теорема. Для дифференцируемой функции с производной, не равной нулю, производная обратной функции равна обратной величине производной данной функции, т.е. .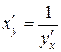

Производная логарифмической функции:

; .

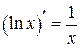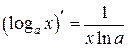Производная показательной функции:

;

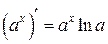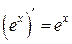
Производная степенной функции:

.

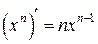Производные тригонометрических функций:

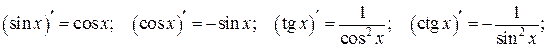
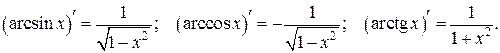
Производная неявной функции 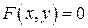получается дифференцированием обеих частей уравнения, рассматривая y как функцию от x, а затем из полученного уравнения находится :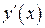