Параметры, характеризующие качество линейной модели
Качеством модели регрессии называется адекватность построенной модели исходным (наблюдаемым) данным.
Для оценки качества модели регрессии используются специальные показатели.
Качество линейной модели парной регрессии характеризуется с помощью следующих показателей:
1) парной линейный коэффициент корреляции, который рассчитывается по формуле: 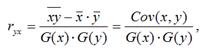
где G(x) – среднеквадратическое отклонение независимой переменной;
G(y) – среднеквадратическое отклонение зависимой переменной.
Также парный линейный коэффициент корреляции можно рассчитать через МНК (метод наименьших квадратов) - оценку коэффициента модели регрессии 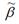 по формуле:
по формуле:
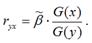
Парный линейный коэффициент корреляции характеризует степень тесноты связи между исследуемыми переменными. Он рассчитывается только для количественных переменных. Чем ближе модуль значения коэффициента корреляции к единице, тем более тесной является связь между исследуемыми переменными. Данный коэффициент изменяется в пределах [-1; +1]. Если значение коэффициента корреляции находится в пределах от 0 до 1, то связь между переменными прямая, т. е. с увеличением независимой переменной увеличивается и зависимая переменная, и наборот. Если коэффициент корреляции находится в пределах от -1 до 0, то связь между переменными обратная, т. е. с увеличением независимой переменной уменьшается зависимая переменная, и наоборот. Если коэффициент корреляции равен нулю, то связь между переменными отсутствует. Если коэффициент корреляции равен единице или минус единице, то связь между переменными существует функциональная связь, т. е. изменения независимой и зависимой переменных полностью соответствуют друг другу.
2) коэффициент детерминации рассчитывается как квадрат парного линейного коэффициента корреляции и обозначается как R2xy . Данный коэффициент характеризует в процентном отношении вариацию зависимой переменной, объяснённой вариацией независимой переменной, в общем объёме вариации.
Качество линейной модели множественной регрессии характеризуется с помощью показателей, построенных на основе теоремы о разложении дисперсий.
Теорема. Общая дисперсия зависимой переменной может быть разложена на объяснённую и необъяснённую построенной моделью регрессии дисперсии:
G2(y)=σ2(y)+δ2(y), Dобщ.=∑1n(yi-yср)2
где G2(y) – это общая дисперсия зависимой переменной;
σ2(y) – это объяснённая (фактическая) с помощью построенной модели регрессии дисперсия переменной у, которая рассчитывается по формуле:
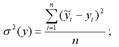 Dфакт.=∑1n(yx-yср)2
Dфакт.=∑1n(yx-yср)2
δ2(y) – необъяснённая или остаточная дисперсия переменной у, которая рассчитывается по формуле:
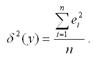 Dост.=∑1n(yi-yx)2
Dост.=∑1n(yi-yx)2
С использованием теоремы о разложении дисперсий рассчитываются следующие показатели качества линейной модели множественной регрессии:
1) множественный коэффициент корреляции между зависимой переменной у и несколькими независимыми переменными хi:
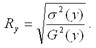
Данный коэффициент характеризует степень тесноты связи между зависимой и независимыми переменными. Свойства множественного коэффициента корреляции аналогичны свойствам линейного парного коэффициента корреляции.
2) теоретический коэффициент детерминации рассчитывается как квадрат множественного коэффициента корреляции:
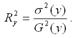
Данный коэффициент характеризует в процентном отношении вариацию зависимой переменной, объяснённой вариацией независимых переменных;
3) показатель
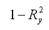
характеризует в процентном отношении ту долю вариации зависимой переменной, которая не учитывается в построенной модели регрессии;
4) среднеквадратическая ошибка модели регрессии (Mean square error – MSE):
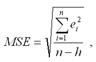
где h– это количество параметров, входящих в модель регрессии.
Если показатель среднеквадратической ошибки окажется меньше показателя среднеквадратического отклонения наблюдаемых значений зависимой переменной от модельных значений β(у), то модель регрессии можно считать качественной.
Показатель среднеквадратического отклонения наблюдаемых значений зависимой переменной от модельных значений рассчитывается по формуле:
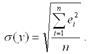
5) показатель средней ошибки аппроксимации рассчитывается по формуле:
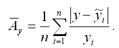
Если величина данного показателя составляет менее 6-7%, то качество построенной модели регрессии считается хорошим. Максимально допустимым значением показателя средней ошибки аппроксимации считается 12-15 %.
