Мысал: Екі қойылымның көбейтіндісі.
Анықтама.Егер n-реттті алмастыруды бірінің астына бірін жазсақ, n-ретті қойылым шығады.
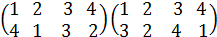 =
= 
47. Анықтауыштың негізгі қасиеттері. (дәлелдеумен)
1)Егер анықтауышта екі жолдың(бағанның) орындарын ауыстырсақ онда анықтауыштың таңбасы қарама-қарсыға ауысады.
Дәлелдеу. 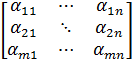 =
= 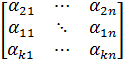
2)Егер матрицаны аударсақ онда оның анықтауышы өзгермейді:| 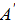 |=|A|
|=|A|
3)Егер анықтауыштың бір жолының(бағанының) ортақ көбейткіші бар болса,онда оны анықтауыштың таңбасының сыртына шығаруға болады.
Дәлелдеу.
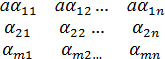 =a
=a  +a
+a 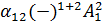 +…a
+…a 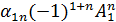 =a|A|
=a|A|
4)Егер матрицаның қандай да бір жолына(бағанына) басқа жолды (бағанды) санға көбейтіп алып қоссақ, онда анықтауыш өзгермейді
5)Егер анықтауыштың екі жолы(бағаны ) бірдей болса, онда анықтауыш нөлге тең болады.
6)Блокты үшбұрышты матрицалардың анықтауышы диагональдік блоктарының анықтауыштарының көбейтіндісіне тең болады.
7)Егер А матрицасының жолдары немесе бағандары сызықтық тәуелді болса, онда анықтауыш 0-ге тең.
Сызықтық кеңістіктің анықтамасы. Мысалдар. Сызықтық кеңістіктердің базисы және өлшемі. Сызықтық кеңістіктердің өлшемі туралы теорема.
(P, +, *) P өрісі берілген (X, 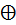 ,
,  ) веторлар жиыны берілсін ,
) веторлар жиыны берілсін , 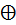 ,
,  <= қосу; санға көбейту векторлардын.<X,P> жұбы сызықтық кеністік деп аталады , егер төмендегі аксиомалар орындалса:
<= қосу; санға көбейту векторлардын.<X,P> жұбы сызықтық кеністік деп аталады , егер төмендегі аксиомалар орындалса:
1. 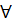 x,y
x,y 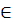 X x
X x 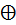 y= y
y= y 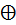 x
x
2. 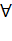 x,y,z
x,y,z 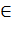 X (x
X (x 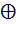 y)
y) 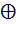 z = x
z = x 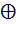 (y
(y 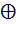 z )
z )
3. 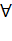 x
x 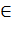 X
X  X x
X x 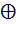 y= y
y= y 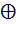 x=
x= 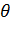
4. 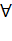 x
x 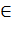 X
X 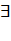 y
y 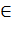 X x
X x 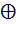 y= y
y= y 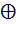 x=
x= 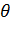
5. 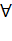 x
x 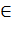 X 1
X 1  x=x
x=x
6.  P
P 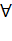 x
x 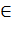 X (
X ( 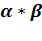 )
)  x=
x=  (
( 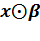 )
)
7. 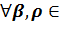 P
P 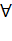 x
x 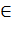 X (
X ( 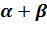 )
)  x=
x= 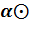 x
x 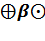 x
x
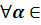 P
P 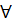 x,y
x,y 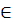 X
X 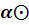 ( x
( x 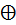 y)=
y)= 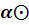 x
x 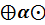 yМысалы: 1. (Mn*k (
yМысалы: 1. (Mn*k (  ),t,*) – сызықтық кеңістік; 2. (М1*n
),t,*) – сызықтық кеңістік; 2. (М1*n 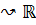 n)- сызықтық кеңістік. <X,P> сызықтық кеністік а1,a2,a3,…,ak
n)- сызықтық кеңістік. <X,P> сызықтық кеністік а1,a2,a3,…,ak 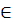 XL(а1,a2,a 3,…,ak)={
XL(а1,a2,a 3,…,ak)={ 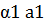 +
+ 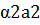 +…
+… 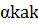 / α1,α2,αk
/ α1,α2,αk 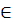 P}-бұл сызықтық қабықша(a1…ak), {b1…bn} векторлар жуйесинің сызықтық эквиваленті деп аталады. Келесі шарттар орындалса: 1.
P}-бұл сызықтық қабықша(a1…ak), {b1…bn} векторлар жуйесинің сызықтық эквиваленті деп аталады. Келесі шарттар орындалса: 1. 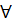 i ai
i ai 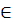 L{b1…bn} 2.
L{b1…bn} 2. 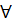 j aj
j aj 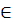 L(a1…an)a1,a2…ak сызықтық векторлар базисі деп аталады егер келесі 2 шарт орындалса:1.{a1…ak} сызықтық тәуелсіз 2.
L(a1…an)a1,a2…ak сызықтық векторлар базисі деп аталады егер келесі 2 шарт орындалса:1.{a1…ak} сызықтық тәуелсіз 2. 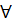 b
b 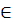 X b
X b 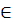 L (ai…ak) сызықты өрнектейді<X,P> c.k. өлшемі деп к санын атаймыз егер кез-келген элемент сызықтық тауелсіз бола тура осы жүйеге Х жиынына(максимал сызықтық тәуелсіз ішкі жүйенін векторларынын саны ) кез келген веторды біріктірсек сызықтық тәуелді жүйе шықса dim x=k.Теорема.(сызықтық кеңістік өлшемі туралы) dim x=n болсын ,онда келесі шарттар эквивалентті: 1)X кеңістігінің веторлар жиынының базисі табылады.
L (ai…ak) сызықты өрнектейді<X,P> c.k. өлшемі деп к санын атаймыз егер кез-келген элемент сызықтық тауелсіз бола тура осы жүйеге Х жиынына(максимал сызықтық тәуелсіз ішкі жүйенін векторларынын саны ) кез келген веторды біріктірсек сызықтық тәуелді жүйе шықса dim x=k.Теорема.(сызықтық кеңістік өлшемі туралы) dim x=n болсын ,онда келесі шарттар эквивалентті: 1)X кеңістігінің веторлар жиынының базисі табылады.
2) X жиынының кез-келген 2 базисінін элементтері саны тең болады.
54.Сызықтық қабықшалар. Ішкі кеңістіктердің қосындысының өлшемі туралы теорема. 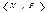 сызықтық кеңістігінде кез келген a1,a2,..,ak векторларының жүйесі берілсін.Осы векторлардан құрылған барлық сызықтық өрнектерден тұратын L(a1,a2,..,ak)⇌{⍺1a1+⍺2a2+…+⍺kak⃓⍺1,⍺2…,⍺k⋴P} жиынын a1a2,..,ak векторларының сызықтық қабықшасы,ал а1,a2,..,ak векторлардын L(a1,a2,...,ak)сызықтық қабықшасының жасаушылары д.а.Ішкі кеңістіктерінің L=L1+L2+…+Lk қосындысы Ɵ вектор үшін a=a+Ɵ жіктелуінің жалғыз болған жағыдайында және тек сол жағдайында ғана тура қосынды б/ы. Дәләлдеу. Қ.Қандайда бір А⋴L векторы үшін a=a+Ɵ жіктеуі бар болсын:a=a1+a2+…+ak және a=a’1+a’2+…+a’k. Бір жіктеуден екіншісін шегеріп,нөлдік вектор үшін Ɵ=(a1-a’1)+(a2-a’2)+..+(ak-a’k) жіктеуін аламыз.Ɵ вектор үшінa=a+Ɵ жіктеуі жалғыз және Ɵ=Ɵ+Ɵ+..+Ɵ болғандықтан, (a1-a’1)=(a2-a’2)=..=(ak-a’k)= Ɵ демек a1= a’1, a2=a’2,…, ak=a’k болады.
сызықтық кеңістігінде кез келген a1,a2,..,ak векторларының жүйесі берілсін.Осы векторлардан құрылған барлық сызықтық өрнектерден тұратын L(a1,a2,..,ak)⇌{⍺1a1+⍺2a2+…+⍺kak⃓⍺1,⍺2…,⍺k⋴P} жиынын a1a2,..,ak векторларының сызықтық қабықшасы,ал а1,a2,..,ak векторлардын L(a1,a2,...,ak)сызықтық қабықшасының жасаушылары д.а.Ішкі кеңістіктерінің L=L1+L2+…+Lk қосындысы Ɵ вектор үшін a=a+Ɵ жіктелуінің жалғыз болған жағыдайында және тек сол жағдайында ғана тура қосынды б/ы. Дәләлдеу. Қ.Қандайда бір А⋴L векторы үшін a=a+Ɵ жіктеуі бар болсын:a=a1+a2+…+ak және a=a’1+a’2+…+a’k. Бір жіктеуден екіншісін шегеріп,нөлдік вектор үшін Ɵ=(a1-a’1)+(a2-a’2)+..+(ak-a’k) жіктеуін аламыз.Ɵ вектор үшінa=a+Ɵ жіктеуі жалғыз және Ɵ=Ɵ+Ɵ+..+Ɵ болғандықтан, (a1-a’1)=(a2-a’2)=..=(ak-a’k)= Ɵ демек a1= a’1, a2=a’2,…, ak=a’k болады.
