Уравнения механической системы

Математические выражения, связывающие параметры движения сооружений и воздействий на него, называются уравнениями движения сооружений. Имеются три метода вывода уравнения движения – метод динамического равновесия, принцип возможных (виртуальных) перемещений и закон сохранения энергии при колебаниях (принцип Гамильтона).

Решение сложных задач динамики может быть сведено к решению более простых задач статики, если к силам действующим на систему материальных точек или деформируемую систему, добавить силы инерции.

Силой инерции называется воображаемая сила, равная по величине произведению массы точки на ее ускорение и имеющая направление прямо противоположное ускорению

Второй з-н Ньютона связывающий силу Р и вызываемое ею ускорение записывается в виде:

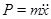(II.1)

Понятие силы инерции можно ввести, если равенство (II.1) переписать в форме

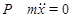(II.2)

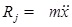или Р+Rj=0 (II.3), где

Формулу (II.3) можно рассматривать как запись условия равенства нулю суммы проекций всех сил, действующих на массу m. При этом под R_j понимается сила прикладываемая к массе, которая условно рассматривается как находящаяся в покое. Это и есть сила инерции, а принцип Даламбера состоит в том, что уравнение движения типа (II.2) можно получить путем составления обычных уравнений равновесия типа (II.3).

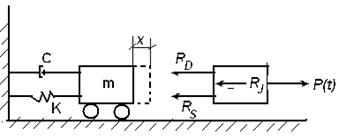
Рис. Модель системы с одной степенью свободы.

Равновесие этой системы от воздействия переменной во времени силы P_t обеспечивается тремя силами сопротивления: инерционная R_j, диссипативная R_D и восстанавливающая R_S. Условие равновесия этих сил:

R_J + R_D + R_S = P(t) (II.4)

Упругая восстанавливающая сила характеризуется жесткостью пружины К на перемещение х:

R_S = k x (II.5a)

Сила инерции равна произвдению массы на ускорение

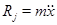(II.5б)

При вязком затухании диссипативная сила RD определяется произведением постоянной затухания С на скорость системы:

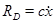(II.5в)

После подстановки этих выражений в формулу (II.4) получаем уравнение движения рассматриваемой системы с одной степень свободы:

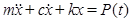
(II.6)

Левая часть этого уравнения движения определяет сопротивляемость (реакцию) деформируемой системы, а правая часть характеризует закон изменения (модель) воздействия.

Свободные или собственные колебания происходят в изолированной системе после внешнего возмущения. Характер колебательного процесса определяется внутренними силами системы, зависящими от физического строения.

Идеализированные системы в которых запас механической энергии остается постоянным называется консервативными системами.

Лекция 13, 14