Ограничения вида неравенств
| (3.3) |
Z = f (x1 ,x2 ,…, xn ) max,
| (3.4) |
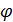 1(x1 ,x2 ,…, xn ) =
1(x1 ,x2 ,…, xn ) = 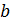 1,
1, 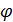 2(x1 ,x2 ,…, xn ) =
2(x1 ,x2 ,…, xn ) = 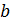 2,
2,
- - - - - - - - - - - - - - -
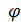 m(x1 ,x2 ,…, xn ) =
m(x1 ,x2 ,…, xn ) = 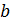 m,
m,
Для ее решения будем использовать метод множителей Лагранжа. Пусть λ1, λ2,…, λm - некоторые числа. Составим функцию Лагранжа 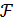 :
:
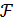 (x1 ,x2 ,…, xn, λ1, λ2,…, λm ) = f (x1 ,x2 ,…, xn ) +
(x1 ,x2 ,…, xn, λ1, λ2,…, λm ) = f (x1 ,x2 ,…, xn ) + 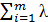 i [b1 -
i [b1 - 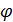 1(x1 ,x2 ,…, xn )].
1(x1 ,x2 ,…, xn )].
Задача на нахождение условного экстремума функции f сводится к задаче нахождения безусловного экстремума функции Лагранжа 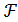 .
.
Необходимым условием экстремума функции Лагранжа является равенство нулю ее частных производных:
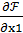 =
= 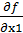 -
- 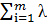 i
i 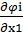 = 0,
= 0,
| (3.5) |
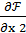 =
= 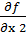 -
- 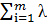 i
i 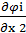 = 0,
= 0,
- - - - - - - - - - - - - - - - - - - - - - - - -
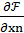 =
= 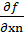 -
- 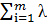 i
i 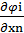 = 0,
= 0,
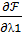 = b1 -
= b1 - 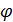 1(x1 ,x2 ,…, xn ) = 0,
1(x1 ,x2 ,…, xn ) = 0,
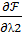 = b2 -
= b2 - 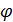 2(x1 ,x2 ,…, xn ) = 0,
2(x1 ,x2 ,…, xn ) = 0,
- - - - - - - - - - - - - - - - - - - - - - - - - - -- - - - - - -
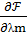 = bm -
= bm - 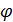 m(x1 ,x2 ,…, xn ) =0.
m(x1 ,x2 ,…, xn ) =0.
Получили систему n + m уравнений с n + m неизвестными x1 ,x2 ,…, xn ; λ1, λ2,…, λm. Для выпуклых (вогнутых) функций решение системы уравнений единственное (если конечно, оно вообще существует). Пусть решением системы является следующая совокупность значений переменных: xo 1, xo2,…, xon ; λo1, λo2,…, λom. Это решение, дающее экстремум функции Лагранжа, состоит из двух частей:
оптимальное решение задачи xo=(xo 1,xo2,…, xon) и оптимальный вектор множителей Лагранжа λo=(λo1, λo2,…, λom).
Вообще-то нам необходимо было найти оптимальное решение задачи (3.3), (3.4), то ест решение xo. Но, как увидим далее, значения множителей Лагранжа, соответствующие оптимальному плану xo, не являются излишними. Напротив, с их помощью можно получить дополнительную ценную информацию об оптимальном xo. Остановимся на значении множителей Лагранжа в плановой практике.
Пусть условия (3.3), (3.4) отражают следующую задачу производства x1 ,x2 ,…, xn для некоторого предприятия, который обеспечивал бы ему максимум прибыли f (x1 ,x2 ,…, xn )
и соответствовал бы балансу потребности и лимита по всем видам производственных ресурсов. Если потребность в ресурсе на предприятии составляет 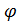 i(x1 ,x2 ,…, xn ) единиц, лимит этого ресурса составляет bi единиц, то можно утверждать, что план производства должен удовлетворять равенствам
i(x1 ,x2 ,…, xn ) единиц, лимит этого ресурса составляет bi единиц, то можно утверждать, что план производства должен удовлетворять равенствам
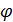 i (x1 ,x2 ,…, xn ) = bi , i=1,2,…,m.
i (x1 ,x2 ,…, xn ) = bi , i=1,2,…,m.
Очевидно, что оптимальное решение задачи (3.3) и (3.4) зависит от правых частей ограничений (3.4). Это значит, что компоненты оптимального плана xo 1,xo2,…, xon зависят от лимитов ресурсов b1, b2,…, bm. Понятно, что и оптимальное значение целевой функции
Zo= f (xo1,xo2,…, xon) также будет зависеть от b1, b2,…, bm. Найдем числовое выражение зависимости оптимального значения целевой функции Z от лимитов ресурсов b1, b2,…, bm.
Для измерения чувствительности оптимального значения целевой функции Zo от изменения лимитов ресурсов bi воспользуемся частной производной 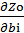 .
.
Докажем, что 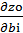 = λoi , i=1,2,…,m.
= λoi , i=1,2,…,m.
Компоненты оптимального плана xoj есть некоторые функции от bi , i=1,2,…,m:
xoj = xoj (b1, b2,…, bm) , j=1,2,…,n.
Поэтому Zo есть сложная функция вида
Zo= Zo(b1, b2,…, bm)= Zo[xo1(b1, b2,…, bm),…, xon(b1, b2,…, bm)].
Используя правило дифференцирования сложной функции, получим
| (3.6) |
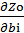 =
= 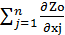 ∙
∙ 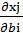 .
. Продифференцируем левую и правую части равенства fk (xo1,xo2,…, xon)=bk по bi, получим
| (3.7) |
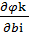 =
= 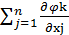 ∙
∙ 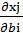 =
= 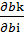 = 1, 2, если k = i если k ≠ i.
= 1, 2, если k = i если k ≠ i. Умножим на λok и просуммируем по k, получим
λoi - 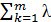 ok
ok 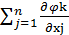 ∙
∙ 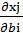 =
= 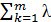 ok
ok 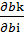 .
.
Отсюда имеем
| (3.8) |
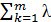 ok
ok 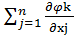 ∙
∙ 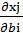 = 0.
= 0. Сложив(3.6) и (3.8), получим
| (3.9) |
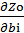 = λoi +
= λoi + 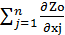 ∙
∙ 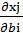 -
- 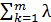 ok
ok 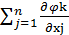 ∙
∙ 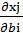 .
. Два последних слагаемых в первой части (3.9) вместе равны нулю. Покажем это:
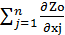 ∙
∙ 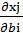 -
- 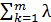 ok
ok 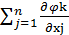 ∙
∙ 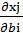 =
= 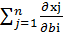 ∙
∙ 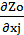 -
- 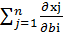 ∙
∙ 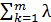 ok
ok 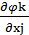 =
=
= 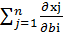 (
( 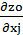 -
- 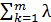 ok
ok 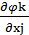 ).
).
Но согласно необходимому условию экстремума функции Лагранжа
| (3.10) |
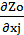 -
- 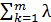 ok
ok 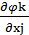 = 0,
= 0,
| (3.11) |
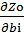 = λoi , i=1,2,…,m.
= λoi , i=1,2,…,m. Таким образом, метод множителей Лагранжа, помимо того, что дает решение задачи ВП с ограничениями в виде равенств, позволяет также проанализировать, насколько оптимальное значение целевой функции чувствительно к изменениям констант ограничений. Например, если какой-то множитель Лагранжа равен нулю, то небольшие изменения соответствующей константы ограничений не окажут никакого влияния на оптимальное значение целевой функции. Если некоторая константа bi увеличится на одну единицу, то при λoi >0 множитель Лагранжа λoi показывает, что оптимальное значение целевой функции Zo увеличится на λoi единицу (в задаче на максимум). Обратим внимание на то, что при этом нет необходимости решать новую задачу ВП, у которой правая часть ограничения i равна bi + 1.
В целом можно сделать вывод, что практическое значение равенства (3.11) в том, что мы легко можем оценить, как изменится оптимальное значение целевой функции при малом изменении лимитов ресурсов. По-другому говоря, множители Лагранжа λoi являются оценками ресурсов b1, b2,…, bm.
Рассмотрим теперь способ решения задачи выпуклого программирования в случае ограничений неотрицательности и ограничений в виде равенств .
| (3.12) |
Z = f (x1 ,x2 ,…, xn ) max,
| (3.13) |
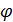 1(x1 ,x2 ,…, xn ) =
1(x1 ,x2 ,…, xn ) = 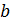 1,
1, 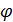 2(x1 ,x2 ,…, xn ) =
2(x1 ,x2 ,…, xn ) = 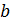 2,
2,
- - - - - - - - - - - - - - -
| (3.14) |
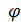 m(x1 ,x2 ,…, xn ) =
m(x1 ,x2 ,…, xn ) = 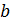 m,
m, xj ≥ 0, j=1,2,…,n.
Вновь для решения задачи применим метод множителей Лагранжа.
Составим функцию Лагранжа
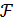 (x1 ,x2 ,…, xn, λ1, λ2,…, λm ) = f (x1 ,x2 ,…, xn ) +
(x1 ,x2 ,…, xn, λ1, λ2,…, λm ) = f (x1 ,x2 ,…, xn ) + 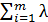 1 [b1 -
1 [b1 - 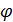 1(x1 ,x2 ,…, xn )].
1(x1 ,x2 ,…, xn )].
| (3.15) |
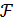 будет записываться так:
будет записываться так:
| (3.16) |
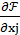 = 0, j=1,2,…,n,
= 0, j=1,2,…,n, λi 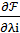 =0, i=1,2,…,m.
=0, i=1,2,…,m.
Запишем условие (3.15) в развернутом виде (случай задачи на максимум):
| (3.17) |
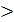 0, то
0, то 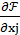 = 0; если xj
= 0; если xj 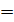 0,то
0,то 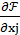 ≤ 0;
≤ 0; или, если xj 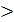 0, то
0, то 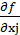 -
- 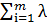 i
i 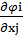 = 0; если xj
= 0; если xj 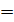 0, то
0, то 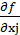 -
- 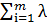 i
i 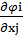 ≤ 0.
≤ 0.
Что касается условия (3.16), то относительно λi оно является тождеством. Действительно
λi 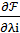 = λi ( bi -
= λi ( bi - 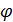 i(x1 ,x2 ,…, xn )) = 0.
i(x1 ,x2 ,…, xn )) = 0.
Согласно условию задачи 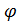 1(x1 ,x2 ,…, xn )=bi ,поэтому λi ( bi -
1(x1 ,x2 ,…, xn )=bi ,поэтому λi ( bi - 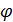 i(x1 ,x2 ,…, xn )) = 0
i(x1 ,x2 ,…, xn )) = 0
Условия bi - 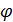 i(x1 ,x2 ,…, xn ) добавляются к условиям (3.17). Получившаяся система n+m неизвестными позволит решить задачу (3.12)-(3.14).
i(x1 ,x2 ,…, xn ) добавляются к условиям (3.17). Получившаяся система n+m неизвестными позволит решить задачу (3.12)-(3.14).
