Теориялық бөлімі
АРЖ зерттеу үшін қолданылатын, реттеуші сигналдар типтік әсерлер деп аталады. Олар әр түрлі жүйелердің қасиеттерін бастапқы шарттары тең және біркелкі кірістік сигналдар кезінде салыстыруға мүмкіндік береді. Әдетте типтік әсерлерге сатылы (өзгеріс) А·1(t) немесе Хевисайд функциясы, импульстік А·δ(t) немесе Дирак функциясы, гармоникалық А·sinωt және дәрежелі А·tn әсерлер (функциялар) жатады. А=1 болғанда әсер бірлікті деп аталады [1].
Типтік әсерлер:
1 Сатылы функциясы
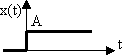 | 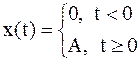 ; A = const ; A = const |
A∙1(t) деп жазылады, А=1 болғанда әсер бірлікті деп аталады.
Лаплас кескіні бойынша L{1(t)} = 1/s.
2 Импульстік функциясы
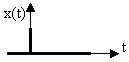 | 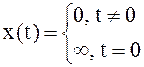 , , 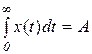 |
А∙δ(t) деп жазылады, А=1 болғанда импульс бірлікті деп аталады.
Лаплас кескіні бойынша 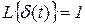 .
.
3 Гармоникалық функциясы
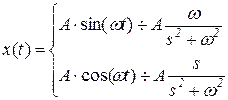 ;
;
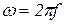 – жиілік, рад/с.
– жиілік, рад/с.
4 Дәрежелі функциясы
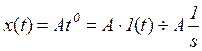 |
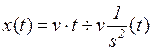 |
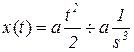 |
негізгі түрі: 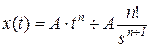
А = 1 (ν = 1, a = 1) болғанда әсер бірлікті деп аталады [3].
Рұқсат етілген қателігі бар, кез - келген уақыт функциясын, салмақ коэффициенттері сәйкес болып келетін типтік әсерлер жиынтығына жіктеуге болады. Онда суперпозициялық қағидасы бойынша осы әсер реакциясы - жеке әсерлерге (есептеу қағидасы белгілі) сызықты жүйелер реакциясының қосындысы арқылы анықталады.
h(t) өтпелі функциясы деп, нөлдік бастапқы шарттағы 1(t) бірлік өзгерісіне деген жүйенің реакциясын айтады. Ерікті шаманың өзгеруі кезінде туындайтын реакцияны екпін қисығы деп атайды.
g(t) импульстік (салмақты) функциясы деп, нөлдік бастапқы шарттағы δ(t) бірлік импульсіне деген жүйенің реакциясы аталады.
Лапластың түрлендіруі дифференциалдық теңдеулерді шешудің негізгі инженерлік әдісі, яғни АРЖ – нің уақыт бойынша сипатын зерттеу болып табылады. Мұнда дифференциалдау мен интегралдау операциялары қарапайым алгебралық операцияларымен - s комплекстік айнымалысына көбейту және бөлумен, алмастырылады. Операторлық беріліс функциясы (БФ) бір кіріс және бір шығыс әдісі бойынша операторлық аймақта жүйені сипаттаудың негізгі түрі болып табылады [1].
W(s) - беріліс функциясы төмендегі әдістермен алынуы мүмкін:
- уақыт және жиіліктік сипаттамалар бойынша;
- құрылымдық сызба бойынша;
- дифференциалдық теңдеу бойынша.
W(s) беріліс функциясы деп, нөлдік бастапқы шарттағы Лаплас бойынша кескінінің Y(s) шығыс шамасының X(s) кіріс шамасына қатынасы аталады. Әдетте m ≤ n, мұндағы n – жүйенің реті.
Жүйенің дифференциалдық теңдеуі арқылы W(s) БФ:
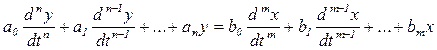
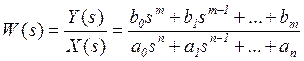
Беріліс функциясы b0/a0 коэффициентіне дейін дәлдікпен, алымындағы полиномның түбірлерімен (нөлдермен) және бөліміндегі полиномының түбірлерімен (полюстермен) көрсетілуі мүмкін [3].
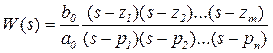
Уақыт функциясының түп-нұсқасының бастапқы және соңғы мәндері туралы теоремаға сәйкес өтпелі сипаттамасының бастапқы h(0) және соңғы (орнатылған) h( 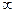 ) мәндері сәйкесінше беріліс функциясының sn дәрежелі болғандағы алымы мен бөліміндегі коэффициенттердің қатынасына және БФ бос мүшелерінің қатынасына (kорн немесе k(∞) орнатылған режиміндегі күшейту коэффициентіне) тең.
) мәндері сәйкесінше беріліс функциясының sn дәрежелі болғандағы алымы мен бөліміндегі коэффициенттердің қатынасына және БФ бос мүшелерінің қатынасына (kорн немесе k(∞) орнатылған режиміндегі күшейту коэффициентіне) тең.
Бастапқы мәні: 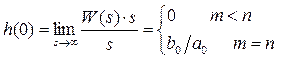
Соңғы мәні: 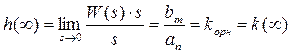 .
.
