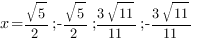Однородные уравнения

Уравнения, имеющие структуру однородного, могут встретиться при решении показательных, логарифмических и тригонометрических уравнений, поэтому ее нужно уметь распознавать.

Однородные уравнения имеют такую структуру: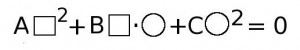

В этом равенстве А, В и С – числа, а квадратиком и кружочком обозначены одинаковые выражения. То есть в левой части однородного уравнения стоит сумма одночленов, имеющих одинаковую степень ( в данном случае степень одночленов равна 2), и свободный член отстутствует.

Чтобы решить однородное уравнение, разделим обе части на

Или на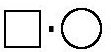

Или на

Внимание! При делении правой и левой части уравнения на выражение, содержащее неизвестное, можно потерять корни. Поэтому необходимо проверить, не являются ли корни того выражения, на которое мы делим обе части уравнения, корнями исходного уравнения.

Пойдем первым путем. Получим уравнение:

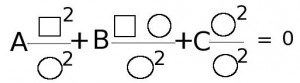Сократим дроби, получим:

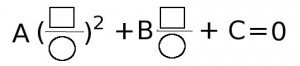
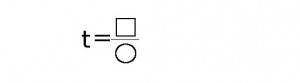
Теперь мы вводим замену переменной:

И решаем квадратное уравнение относительно замены:

.

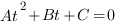Решим уравнение:

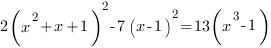
При решении уравнения я обычно придерживаюсь такой тактики: нужно уменьшить количество различных выражений, в состав которых входит неизвестное (принцип «бритвы Оккама» - не нужно множить сущности без нужды), а для этого помогает разложить выражения с неизвестным на множители. Разложим выражение, стоящее в правой части уравнения на множители.

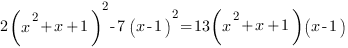
Перенесем все влево, получим:

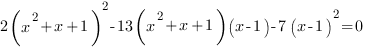
Теперь мы видим, что перед нами однородное уравнение. Разделим обе части уравнения на 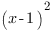, предварительно проверив, что х=1 не является корнем исходного уравнения.

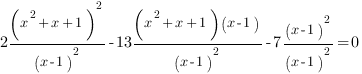
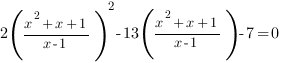
Теперь самое время ввести замену переменной:

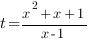
Получим квадратное уравнение:

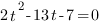
Ответ: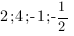

6.

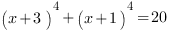
Это уравнение имеет такую структуру:

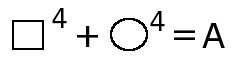Решается с помощью введения вот такой замены переменной:

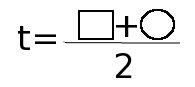В нашем уравнении 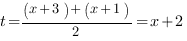,тогда 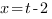. Введем замену:

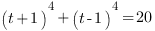
Теперь возведем каждую скобку в четвертую степень, используятреугольник Паскаля:

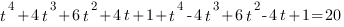
Упростим выражение и получим биквадратное уравнение относительно t:

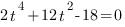
Ответ: 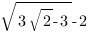или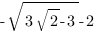

7.

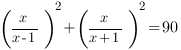
Это уравнение имеет такую структуру: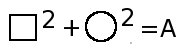

Чтобы его решить, нужно в левой части уравнения выделить полный квадрат.

Чтобы выделить полный квдарат, нужно прибавить или вычесть удовоенное произведение. Тогда мы получим квадрат суммы ли разности. Для удачной замены переменной это имеет определяющее значение.

Начнем с нахождения удвоенного произведения. Именно оно будет ключиком для замены переменной. В нашем уравнении удвоенное произведение равно

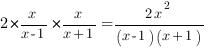
Теперь прикинем, что нам удобнее иметь – квадрат суммы или разности. Рассмотрим, для начала сумму выражений:

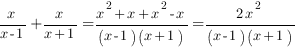
Отлично! это выражении в точности равно удвоенному произведению. Тогда, чтобы в скобках получить квадрат суммы, нужно прибавить и вычесть удвоенное произведение:

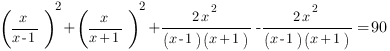[/pmath]

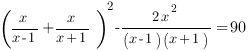
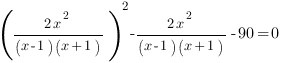
Введем замену: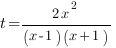

Получим квадратное уравнение:

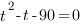
Ответ: