Дәріс. Салу есептерінің классификациясы негізінде шығару әдістерін таңдау.

Планиметрия курсынан стереометрия курсына көшкен Х сынып оқушыларының бұған дейiнгi геометриялық фигуралардың қасиеттерi туралы барлық бiлiмдерi мен түсiнiктерi жазықтыққа негiзделген. Ал үш өлшемдi кеңiстiкте жазықтық жеке фигураға айналады және сонымен қатар өзiнiң қасиеттерiмен бiрге жазық фигураларды жасаушы болады.

Оқушыға жазықтық бейнесiн үш өлшемдi кеңiстiкте елестету, кеңiстiкте екi, үш және одан да артық жазықтықтарды орналастыру қиынға соғады. Осы жағдайларды ескере отырып, стереометрия курсында алдымен негiзгi фигуралардың метрикалық емес қасиеттерi баяндалады. Яғни, үш өлшемдi кеңiстiкте негiзгi фигуралардың өзара орналасу жағдайларына талдаулар жасалып, олардың барлық мүмкiн жағдайлары зерттеледi.

Негiзгi фигуралардың өзара орналасуынан құралған кеңiстiк конфигурациясын ойша елестету және елестегi кеңiстiк образдарына түрлi операциялар қолдану арқылы оқушылардың кеңiстiктiк түсiнiктерiн қалыптастыру – елестету арқылы орындалатын салу есептерiн шығару негiзiнде жүзеге асырылатындығы айтылады. Ал бұндай түрдегi есептер орта мектептiң геометрия оқулықтарында жеткiлiктi ұсынылған. Олар “…жүргiзiңiз” деген конструктивтi тұжырымдамамен және “…жүргiзуге болатындығын дәлелде” сияқты дәлелдеуге берiлген есептер түрiнде берiледi. Мұндағы дәлелдеуге берiлген есептер де конструктивтi жолмен, яғни елестету арқылы орындалатын салулар бойынша шығарылады.

Бұл параграфта стереометрия курсының алғашқы “стереометрия аксиомалары”, “түзулер және жазықтықтардың паралельдiгi”, “түзулер және жазықтықтардың перпендикулярлығы” тарауларындағы түзулер және жазықтықтардың өзара орналасуы мен белгiлi бiр шарттарды қанағаттандыратын түзу немесе жазықтықтың бар болуын дәлелдеуге берiлген салу есептерiне классификация жасалды. Салу есептерiнiң берiлу ерекшелiктерiне қарай, оны шығару барысында қолданылатын жалпы тәсiлдерге талдау жасалып, оқушыларды бұл тәсiлдердiң қажеттiсiн дұрыс таңдай бiлуге және осындай есептердi шығаруда жиi пайдалануға болатын кейбiр дербес тәсiлдердi қолдануға үйрету әдiстемесiн қарастырамыз.

Көп жылдарғы тәжiрибе көрсетiп отырғандай геометрияның планиметрия курсынан стереометрия курсына көшу, Х сынып оқушыларына үлкен қиындықтар туғызады. Ол әсiресе стереометрияның алғашқы тараулары есептерiн шығару кезiнде ерекше байқалады.

Оқушылардың бұл қиындықтарды оңай жеңуiне көмек беру үшiн, есептердiң әртүрлi кластарын шығарудың жалпы әдiстерi көрсетiледi. Есептiң шығарылу жолына талдау жасай отырып, оқушылар назарын келесi есептердi шығаруға қажеттi бiлiмдерге аудару керек. Ондай бiлiмдерге қандайда бiр аксиомалар, теоремалар, анықтамалар мен қатар, есептердi шығару үрдiсiнде қолданылған тәсiлдердi де жатқызуға болады. Яғни, есептiң берiлу ерекшелiгi мен оған сәйкес шығару тәсiлiн таңдап алу жолдарына назар аударылып отырса, оқушы кейiн кездесетiн осыған ұқсас есептер класын ажырата алып, оны шығаруда қай тәсiлдi пайдалану керектiгiн бiлетiн болады.

Оқушыларға стереометриялық салу есептерiнiң планиметриялық салу есептерiнен ерекшелiгi мен оның мәнiн ашып көрсету мақсатында және кеңiстiктегi салуларды орындаудың жалпы схемасын түсiндiру үшiн алғашқы теоремаларды (аксиома салдарларын) дәлелдеудi оқулықта көрсетiлгендей, талдау жасамай-ақ, салуды дәлелдеумен бiрге қарастыратын ықшамдатылған схемасы түрiнде емес, салу есептерiн шығарудың толық схемасы (талдау, салу, дәлелдеу, зерттеу) бойынша жүргiзудiң дұрыс екендiгiн тәжiрибе дәлелдедi. Және кез келген салу есебiнiң мазмұны мынадай үш бөлiктен: а) берiлген элементтерден; ә) ненi салу керектiгiнен; б) есеп шығарылатын құралдардан – тұратындығын ескере отырып, оқулықтағы алғашқы есептердi шығару барысында осы мәселелердi ашып көрсету керек. Мысалы. Берiлген екi түзудiң қиылысу нүктесi арқылы олармен бiр жазықтықта жатпайтын үшiншi түзу жүргiзуге бола ма? Жауабын түсiндiрiңдер. Мұндағы:

а) берiлген элементтер - aÇb=A, (aÇb)ºa;

ә) ненi салу керек - AÎc, cËa;

б) есеп шығарылатын құралдар – C₁, C₂, I₂ аксиомалары негiзiнде елестете отырып салу.

Оқушылар осы сияқты нақты нұсқаулармен берiлген салу есептерiн шығаруды, алғашқы теоремаларды дәлелдеудi, толық схема бойынша орындап үйренедi. Салу есептерiн шығару үшiн мынадай мәселелер ретi анықталуы керек:

1) Есеп шартында берiлген элементтердi айқындау;

2) Есеп талабындағы салу керек элементтi белгiлеу;

3) Елестете отырып салу барысын негiздеу үшiн қолданылатын аксиомалар, белгiлi теоремалар және бұған дейiн шығарылған базистiк есептер жиынтығын анықтау;

4) Есептiң берiлу ерекшелiгiне сәйкес оны шығару тәсiлiн таңдап алу.

Мұнда, берiлген элементтердi айқындау және салу керек элементтi белгiлеу - есептiң шартына сәйкес орындалады. Ал, салу барысын негiздеу үшiн қолданылатын аксиомалар, белгiлi теоремалар және бұған дейiн шығарылған базистiк есептер жиынтығын анықтап алу үшiн iзделiндi фигура салынған деп ұйғарамыз. Содан соң, есеп шешiмiне алып келетiн салу ретi анықталғанша салынған деп ұйғарылған фигура мен есеп берiлгендерi арасындағы байланыстарды талдау жасай отырып анықтаймыз. Талдау жасаудың жалпы жоспарын мына түрде құруға болады:

1. Берiлген шарттарды қанағаттандыратын фигураның (түзу, жазықтық, сфера және т.б.) бар болатындығын көрсетуге қажеттi аксиоманы немесе теореманы анықтау;

2. Қандай көмекшi фигураларды (түзулер, жазықтықтар, сфералар және т.с.с.) пайдалану және оларды қандай ретпен жүргiзу қажеттiгiн белгiлеу;

3. 1-2 тұжырымдарды қашан I-V қарапайым есептер алынғанша қайталау.

Талдау жасауды келтiрiлген жалпы жоспар бойынша жүргiзе отырып, мына төмендегi берiлген салу есебiн шығаруда қажеттi аксиомалар мен белгiлi теоремалар жиынтығын және есеп шешiмiне алып келетiн салу ретiн анықтайық.

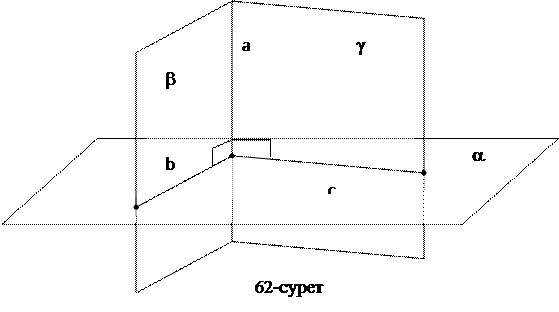
1-есеп. а түзуiнде жатқан А нүктесi арқылы осы түзуге перпендикуляр α жазықтығын жүргiзу.

Талдау.Көрсетiрiлген жалпы жоспар бойынша мынадай талдаулар жасалынады.

а) 1) А нүктесi арқылы өтетiн және а түзуiне перпендикуляр болатын α жазықтығының бар болатындығын көрсетуге қажеттi теорема түзу мен жазықтықтың перпендикулярлық белгiсi болып табылады.

Т е о р е м а. Егер жазықтықты қиятын түзу осы қиылысу нүктесi арқылы өтетiн сол жазықтықта жатқан екi түзуге перпендикуляр болса, ол түзу жазықтыққа перпендикуляр болады.

2) А нүктесi арқылы өтетiн және әрбiрi берiлген а түзуiмен перпендикуляр болатын b және c түзулерiн жүргiзу керек.

ә) 1) Бұндай түзулердiң бар болатындығы планиметрияның мына теоремасы арқылы негiзделедi.

Т е о р е м а. Түзудiң әрбiр нүктесi арқылы оған перпендикуляр түзу жүргiзуге болады және ол тек бiреу ғана болады.

2) Бұл теорема бiр жазықтықта жатқан түзулер үшiн тұжырымдалған. Олай болса, b және c түзулерiн жүргiзу үшiн алдымен а түзуi арқылы β және γ жазықтықтарын жүргiзiп алу қажет.

б) 1) β және γ жазықтықтарын жүргiзу стереометрия курсындағы мына теорема негiзiнде орындалады.

Т е о р е м а. Түзу және онда жатпайтын нүкте арқылы жазықтық жүргiзуге болады және ол тек бiреу ғана болады.

2) Олай болса, β және γ жазықтықтарын жүргiзу үшiн алдымен а түзуiнен тысқары жатқан В және С нүктелерiн алу қажет.

в) 1) а түзуiнен тысқары жатқан әртүрлi В және С нүктелерiнiң бар болуы планиметрияның I₁ - аксиомасы арқылы негiзделедi.

А к с и о м а. Қандай түзудi алсақ та, ол түзуге тиiстi болатын нүктелер де, оған тиiстi емес нүктелер де болады.

Берiлген есеп шешiмiн iздестiру аяқталды. Ендi осы жасалған талдау негiзiнде анықталған аксиомалар мен теоремаларды пайдалана отырып берiлген есептi конструктивтi жолмен шығарайық. Есеп шешiмiне алып келетiн салулар, жасалған талдауға сәйкес, оның соңынан керi қарай орындалады.

Салу.

1) ВÏа нүктесiн салу (62-сурет).

2) а түзуi мен одан тысқары ВÏа нүктесi арқылы β жазықтығын жүргiзу.

3) β жазықтығында А нүктесi арқылы b^а түзуiн жүргiзу.

4) СÏа, СËb нүктесiн салу.

5) а түзуi мен С нүктесi арқылы γ жазықтығын жүргiзу.

6) γ жазықтығында А нүктесi арқылы с^а түзуiн жүргiзу.

Қиылысатын b және c түзулерi арқылы iзделiндi a жазықтығын жүргiзу.

Дәлелдеу. Салуымыз бойынша a^b, a^c болғандықтан АÎа нүктесiнде қиылысатын b, с түзулерi арқылы өтетiн a жазықтығыда a^а және АÎa болғандықтан a жазықтығы iзделiндi жазықтық.

Зерттеу. Жазықтықта берiлген нүкте арқылы түзуге жалғыз түрде ғана перпендикуляр түзу жүргiзуге болатындықтан, ол түзулер арқылы анықталатын a жазықтығы да жалғыз болады. Демек, бұл есептiң шешiмi бар және жалғыз.

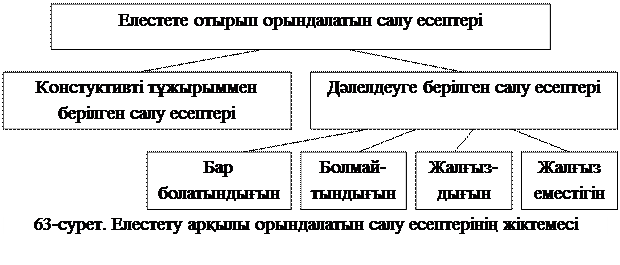
Стереометрия курсының бiрiншi тарауын оқыту барысында-ақ, дәлелдеуге берiлген салу есептерi “Бар болатындығы – Болмайтындығы” және “Жалғыздығы – Жалғыз еместiгi” түрiндегi екi типтегi тұжырымды дәлелдеуге келтiрiледi. Мұндағы (1) қандайда бiр шарттарды қанағаттандыратын түзулердiң немесе жазықтықтардың “бар болатындығы” және ондай түзулердiң немесе жазықтықтардың “жалғыз еместiгi” тұжырымын дәлелдеуге берiлген есептер конструктивтi жолмен шығарылады. Яғни, есеп шешiмi аксиомалар және белгiлi теоремалар немесе шығарылған есептер арқылы негiзделе отырып кеңiстiкте елестету арқылы салынады. Ал, (2) қандайда бiр шарттарды қанағаттандыратын түзулердiң немесе жазықтықтардың “жалғыздығы” және берiлген шарттарды қанағаттандыратын түзулердiң немесе жазықтықтардың “болмайтындығы” тұжырымын дәлелдеу үшiн көп жағдайда қарсы жору әдiсi пайдаланылады. Олай болса, елестету арқылы орындалатын салу есептерiнiң жiктемесiн схема түрiнде мына 63-суреттегiдей беруге болады:

Осы жағдайларға мектеп оқулығынан нақты мысалдар келтiрейiк.

2-есеп. Егер үш нүкте бiр түзудiң бойында жатса, олар арқылы жазықтық жүргiзуге бола ма? Жауабын түсiндiрiңдер.

Шешуi. Яғни, бұл есепте а түзуiнде жататын берiлген А, В, С нүктелерi арқылы a жазықтығын жүргiзуге болатындығын және ондай жазықтықтардың жалғыз еместiгiн көрсету керек (1-жағдай).

Талдау. Берiлген А, В, С нүктелерi а түзуiне тиiстi болсын. Осы а түзуi арқылы қандайда бiр a жазықтығы жүргiзiлген деп ұйғарайық. Бұндай a жазықтығының бар болатындығы мына теорема арқылы негiзделедi.

Т е о р е м а. Түзу және онда жатпайтын нүкте арқылы жазықтық жүргiзуге болады және ол бiреу ғана болады.

Олай болса, a жазықтығын жүргiзу үшiн, а түзуiнен тысқары жатқан D нүктесiн салу керек. Ал, бұндай нүктенiң бар болатындығы I₁-аксиомасы (жоғарыда келтiрiлген) бойынша негiзделедi. Демек, бiр түзудiң бойында жататын үш нүкте арқылы жазықтық жүргiзуге болады. Жүргiзiлген талдауға сәйкес, ондай жазықтықты салу мына ретпен орындалады.

Салу. 1) А, В, С нүктелерi арқылы өтетiн а түзуiнен тысқары жатқан D нүктесiн саламыз.

2) а түзуi және онда жатпайтын D нүктесi арқылы a жазықтығын жүргiземiз.

Дәлелдеу. Салуымыз бойынша А, В және D нүктелерi бiр түзуде жатпайды. Олай болса, бiр түзуде жатпайтын үш нүкте арқылы жазықтық жүргiзуге болады және ол бiреу ғана болады – теоремасы бойынша бұл нүктелер арқылы жазықтық жүргiзуге болады.

Зерттеу. I₁-аксиомасы бойынша, а түзуiнен тысқары жатқан D нүктесiнен басқа да нүктелер алуға болады. Демек, осы нүктелер мен а түзуi арқылы a жазықтығынан басқа да жазықтықтар жүргiзуге болады. Олай болса, бiр түзудiң бойында жатқан үш нүкте арқылы шексiз көп түрде жазықтықтар жүргiзуге болады.

Ендi екiншi жағдайға оқулық бойынша нақты мысал келтiрейiк.

3-есеп. Төрт нүкте бiр жазықтықта жатқан жоқ. Олардың қандайда бiр үшеуi бiр түзудiң бойында жата ала ма? Жауабын түсiндiрiңдер.

Шешуi. Берiлген төрт нүктенiң қандайда бiр үшеуi бiр түзудiң бойында жатқан болсын деп ұйғарайық. Онда осы үш нүкте арқылы өтетiн түзу және төртiншi нүкте арқылы жазықтық жүргiзуге болады. Олай болса, берiлген төрт нүктеде бiр жазықтыққа тиiстi. Ал бұл берiлген есеп шартына қайшы. Демек, төрт нүкте бiр жазықтықта жатпаса, онда осы нүктелердiң ешбiр үшеуi бiр түзуде жатпайды.