Дифференциал функции и его геометрический смысл

Пусть 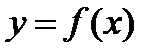дифференцируема на , – производная в некоторой точке отрезка.

Отношение при стремится к определенному числу . Следовательно, отличается от производной на бесконечно малую величину , то есть . при , умножим на :

. (1)

, при постоянном и переменном – бесконечно малая величина первого порядка относительно . Произведение – бесконечно малая высшего порядка относительно , так как

.

состоит из двух слагаемых, из которых первое слагаемое есть (при ), так называемая, главная часть приращения, линейная относительно . Произведение называется дифференциалом функции. Обозначение или .

.

Пример. Найти дифференциал функции .

Решение.

,

, .

Дифференциал независимого переменного сравнивается с его приращением .

,

,

. (2)

Таким образом, приращение функции отличается от дифференциала на величину бесконечно малую высшего порядка относительно . Если , то является бесконечно малой высшего порядка и относительно и

.

,

то есть

.

Выясним геометрический смысл дифференциала, для этого проведем к графику функции 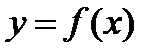в точке касательную, – угол с осью (рис. 5).

Рисунок 5 –

Рассмотрим ординату этой касательной для точки . Отрезок является ординатой точки , ординатой касательной для точки . Назовем приращение ординаты касательной. Покажем, что оно равно .

Из треугольника : , . Согласно геометрическому смыслу производной, , следовательно,

.

Дифференциал функции 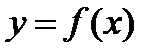в точке 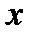равен приращению ординаты касательной.

Пусть и дифференцируемые функции. Тогда

,

,

, .

.

Пример. Найти дифференциал функции .

Решение.

.

Инвариантность формы дифференциала

Если 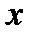– независимая переменная, то дифференциал 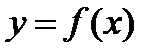имеет следующую форму:

.

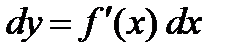Покажем, что эта форма сохраняется, когда 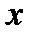– функция. Действительно, если 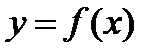, , то – сложная функция.

,

,

что и требовалось доказать.

Дифференциал сложной функции 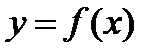, для которой , имеет такой же вид 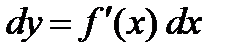, как если бы аргумент 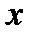был независимой переменной. Это свойство называется инвариантностью формы дифференциала.