Линейный коэффициент детерминации. 8 страница

—

—

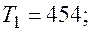
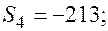
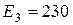
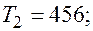
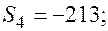
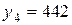
На основе квартальных данных объемов продаж 1993 – 2002гг. была построена аддитивная модель временного ряда. Трендовая компонента имеет вид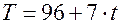

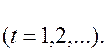
Показатели за 1997 г. приведены в таблице:

Квартал	Фактический объем продаж	Компонента аддитивной модели
трендовая	сезонная	случайная
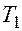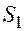				-6
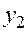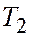				+8
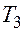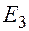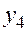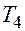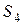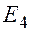ИТОГО:

Отдельные недостающие данные в таблице равны:

+—

—

—

—

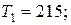
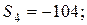
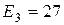
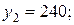
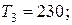
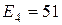
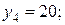
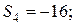
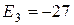
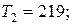
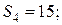
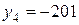
Дана таблица:

Момент времени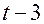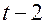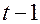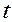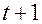
					___

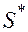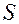где 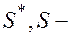ожидаемый и действительный объемы предложения. В соответствии с моделью адаптивных ожиданий, где 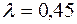, значения 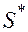соответственно равны:

+—76,75; 87,21; 101,97; 116,83

—78,25; 90,21; 105,25; 120,14

—76,75; 87,21; 105,25;120,14

—78,25; 90,21; 106,60; 122,22

Дана таблица:

Момент времени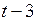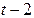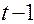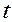
					___

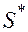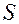где 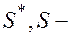ожидаемый и действительный объемы предложения. В соответствии с моделью адаптивных ожиданий, где 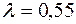, значения 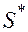соответственно равны:

+—138,25; 152,96; 173,33; 193,50

—136,75; 149,46; 169,63; 189,83

—138,25; 152,96; 169,63; 189,83

—136,75; 149,46; 167,70; 186,74

Дана таблица:

Момент времени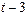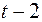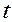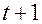
					___

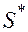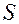где 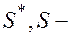ожидаемый и действительный объемы предложения. В соответствии с моделью адаптивных ожиданий, где 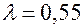, значения 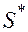соответственно равны:

+—79,25; 101,66; 128,25; 148,46

—78,25; 90,21; 135,46; 120,14

—79,25; 101,66; 135,46;120,14

—78,25; 90,21; 106,74; 122,22

Дана таблица:

Момент времени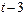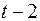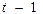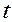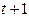
					___

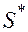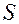где 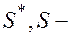ожидаемый и действительный объемы предложения. В соответствии с моделью адаптивных ожиданий, где 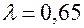, значения 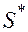соответственно равны:

+—138,25; 155,64; 177,97; 198,79

—136,75; 149,46; 169,63; 189,83

—138,25; 155,64; 169,63; 189,83

—136,75; 149,46; 167,70; 186,74

Дана таблица:

Момент времени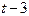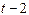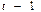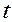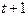
					___

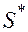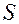где 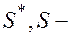ожидаемый и действительный объемы предложения. В соответствии с моделью адаптивных ожиданий, где 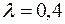, значения 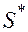соответственно равны:

+—126,00; 133,60; 142,16; 155,30

—125,00; 131,50; 141,50; 152,74

—126,00; 133,60; 141,50; 152,74

—125,00; 131,50; 136,16; 149,70

На основе квартальных данных с 2000 г. по 2004 г. получено уравнение y = - 0,67 + 0,0098 x _t1 – 5,62 x _t2 + 0,044 x _t3

RSS =110,3, ESS = 21,4

В уравнение были добавлены три фиктивные переменные, соответствующие трем первым кварталам года, величина RSS увеличилась до 120,2. Проверьте гипотезу о сезонности (α =0,05):

+—гипотезу об отсутствии сезонности отвергаем, т.к. F=3,76 (>Fкр)

—гипотезу об отсутствии сезонности отвергаем, т.к. F=4,2 (>Fкр)

—гипотезу о наличии сезонности отвергаем, т.к. F=3,76 (<Fкр)

—гипотезу о наличии сезонности отвергаем, т.к. F=4,2 (<Fкр)

На основе квартальных данных с 1991 г. по 2004 г. получено уравнение y = - 0,55 + 0,088 x _t1 – 4,77 x _t2 + 5,4 x _t3

RSS =90,4, ESS = 21,4

В уравнение были добавлены три фиктивные переменные, соответствующие трем первым кварталам года, величина RSS увеличилась до 92. Проверьте гипотезу о сезонности (α =0,05):

+—гипотезу об отсутствии сезонности отвергаем, т.к. F=4,31 (>Fкр)

—гипотезу об отсутствии сезонности отвергаем, т.к. F=3,2 (>Fкр)

—гипотезу о наличии сезонности отвергаем, т.к. F=1,31 (<Fкр)

—гипотезу о наличии сезонности отвергаем, т.к. F=2,2 (<Fкр)

На основе квартальных данных с 2001 г. по 2003 г. получено уравнение y = - 0,55 + 1,8 x _t1 – 2,7 x _t2 + 3,4 x _t3

RSS =115,3, ESS = 10,2

В уравнение были добавлены две фиктивные переменные, соответствующие двум первым кварталам года, величина RSS увеличилась до 120. Проверьте гипотезу о сезонности (α =0,05):

+—гипотезу об отсутствии сезонности отвергаем, т.к. F=8,7 (>Fкр)

—гипотезу об отсутствии сезонности отвергаем, т.к. F=3,2 (>Fкр)

—гипотезу о наличии сезонности отвергаем, т.к. F=8,7 (<Fкр)

—гипотезу о наличии сезонности отвергаем, т.к. F=3,2 (<Fкр)

На основе квартальных данных с 2000 г. по 2002 г. получено уравнение y = 1,55 + 1,4 x _t1 – 0,77 x _t2 + 2,4 x _t3

RSS = 82, ESS = 12

В уравнение были добавлены три фиктивные переменные, соответствующие трем первым кварталам года, величина RSS увеличилась до 90. Проверьте гипотезу о сезонности (α =0,05):

+—гипотезу об отсутствии сезонности отвергаем, т.к. F=4,31 (>Fкр)

—гипотезу об отсутствии сезонности отвергаем, т.к. F=3,2 (>Fкр)

—гипотезу о наличии сезонности отвергаем, т.к. F=1 (<Fкр)

—гипотезу о наличии сезонности отвергаем, т.к. F=2,2 (<Fкр)

Модель зависимости объемов продаж компании от расходов на рекламу имеет вид y = - 0,67 + 4,5 x _t + 3 x _t-1 + 1,5 x _t-2 + 0,5 x _t-3

Краткосрочный, долгосрочный мультипликатор и средний лаг равны:

—краткосрочный 0,5 , долгосрочный 9,5, средний лаг 2,3

+—краткосрочный 4,5 , долгосрочный 9,5, средний лаг 0,791

—краткосрочный -0,67 , долгосрочный 9,5, средний лаг 0,7

Модель зависимости объемов продаж компании от расходов на рекламу имеет вид y = -0,31 + 1,5 x _t + 3 x _t-1 + 4,5 x _t-2 + 0,5 x _t-3

Краткосрочный, долгосрочный мультипликатор и средний лаг равны:

—краткосрочный 0,5 , долгосрочный 9,2, средний лаг 2,3

+—краткосрочный 1,5 , долгосрочный 9,5, средний лаг 0,791

—краткосрочный -0,67 , долгосрочный 9,2, средний лаг 0,7

Модель зависимости объемов продаж компании от расходов на рекламу имеет вид y = 0,27 +1,23 x _t + 0,963 x _t-1 +0,77 x _t-2 + 1,04 x _t-3

Краткосрочный, долгосрочный мультипликатор и средний лаг равны:

—краткосрочный 0,27 , долгосрочный 2,2, средний лаг 2,3

+—краткосрочный 1,23 , долгосрочный 3, средний лаг 2,81

—краткосрочный 1,04, долгосрочный 2, средний лаг 0,7

Модель зависимости объемов продаж компании от расходов на рекламу имеет вид y = -1,6 + 0,5 x _t + 3,3 x _t-1 + 5,5 x _t-2 + 1,5 x _t-3

Краткосрочный, долгосрочный мультипликатор и средний лаг равны:

—краткосрочный 0,5 , долгосрочный 9,2, средний лаг 2,3

+—краткосрочный 0,5 , долгосрочный 10,8, средний лаг 1,46

—краткосрочный -0,67 , долгосрочный 9,2, средний лаг 0,7

На основе квартальных данных получено уравнение множественной регрессии и RSS = 120,32, ESS = 41,4. Для этой же модели были раздельно проведены регрессии на основе данных:

1-й квартал 1991 г. - 1-й квартал 1995 г. и

2-й квартал 1995 г. – 4 квартал 1996 г., соответственно получены следующие значения сумм квадратов остатков ESS₁ = 22,25, ESS₂=12,32. Гипотеза о том, что произошли структурные изменения на уровне α =0,05:

—подтвердилась, т.к. F = 1,8 , что больше F _кр

+—не подтвердилась, т.к. F = 0,8 , что меньше F _кр

—подтвердилась, т.к F = 3,54, что больше F _кр

На основе квартальных данных получено уравнение множественной регрессии и RSS = 110,32, ESS = 21,43. Для этой же модели были раздельно проведены регрессии на основе данных:

1-й квартал 1991 г. - 1-й квартал 1995 г. и

2-й квартал 1995 г. – 4 квартал 1996 г., соответственно получены следующие значения сумм квадратов остатков ESS₁ = 12,25, ESS₂=2,32. Гипотеза о том, что произошли структурные изменения на уровне α =0,05:

—подтвердилась, т.к. F = 1,883 , что больше F _кр

+—не подтвердилась, т.к. F = 1,883 , что меньше F _кр

—подтвердилась, F = 3,54, что больше F _кр

На основе квартальных данных получено уравнение множественной регрессии и RSS = 92,32, ESS = 22,3. Для этой же модели были раздельно проведены регрессии на основе данных:

1-й квартал 1991 г. - 1-й квартал 1995 г. и

2-й квартал 1995 г. – 4 квартал 1996 г., соответственно получены следующие значения сумм квадратов остатков ESS₁ = 6,78, ESS₂=2,2. Гипотеза о том, что произошли структурные изменения на уровне α =0,05:

+—подтвердилась, т.к. F = 8,839 , что больше F _кр

—не подтвердилась, т.к. F = 1,883 , что меньше F _кр

—подтвердилась, т.к F = 3,54, что больше F _кр

На основе квартальных данных с 1991 года по 1996 год с помощью МНК получено следующее уравнение:

Y _t = 1,12 – 0, 0098 x _t1 – 5, 62 x _t2 + 0, 044 x _t3

(2,14) (0,0034) (3,42) (0,009)

В скобках указаны стандартные ошибки, ESS (объясненная сумма квадратов) = 115, 32; RSS (остаточная сумма квадратов) = 25, 43

Когда в уравнение были добавлены три фиктивные переменные, соответствующие первым трем кварталам года, величина ESS выросла до 128, 20. Проверьте гипотезу о наличии сезонности при уровне значимости α = 0,05:

+—гипотеза о наличии сезонности отвергается

—гипотеза о наличии сезонности принимается

—на основе имеющихся данных такую гипотезу проверить невозможно

На основе квартальных данных с 1991 года по 1996 год с помощью МНК получено следующее уравнение:

Y _t = 1,12 – 0, 0098 x _t1 – 5, 62 x _t2 + 0, 044 x _t3

(2,14) (0,0034) (3,42) (0,009)

В скобках указаны стандартные ошибки, ESS (объясненная сумма квадратов) = 116, 32; RSS (остаточная сумма квадратов) = 31, 43

Проверьте значимости коэффициентов и модели в целом при уровне значимости α = 0,05:

—все коэффициенты модели значимы и модель в целом также значима

+—модель в целом значима, но часть коэффициентов незначима

—все коэффициенты незначимы и модель также статистически незначима

—на основе имеющихся данных проверить такие гипотезы невозможно

Тема Система одновременных уравнений. Косвенный МНК (Теоретические вопросы)

Принцип построения системы независимых уравнений состоит в том, что:

+—каждая зависимая переменная рассматривается как функция одного и того же набора факторов

—одни и те же зависимые переменные в одних уравнениях входят в левую часть, в других уравнениях – в правую часть системы

—модель содержит как в правой, так и в левой части эндогенные и экзогенные переменные

Принцип построения системы взаимозависимых уравнений состоит в том, что:

—каждая зависимая переменная рассматривается как функция одного и того же набора факторов

+—одни и те же зависимые переменные в одних уравнениях входят в левую часть, в других уравнениях – в правую часть системы

—модель содержит как в правой, так и в левой части эндогенные и экзогенные переменные

Система одновременных уравнений – это:

+—система взаимозависимых уравнений

—система независимых уравнений

—приведенная форма модели

—система взаимозависимых уравнений или структурная форма модели

Идентификация модели – это:

+—единственность соответствия между приведенной и структурной формами модели

—преобладание эндогенных переменных над экзогенными

—преобладание экзогенных переменных над эндогенными

Модель идентифицируема, если:

+—число коэффициентов структурной модели равно числу коэффициентов приведенной формы модели

—число приведенных коэффициентов меньше числа структурных коэффициентов

—число приведенных коэффициентов больше числа структурных коэффициентов

Модель неидентифицируема, если:

—число коэффициентов структурной модели равно числу коэффициентов приведенной формы модели

+—число приведенных коэффициентов меньше числа структурных коэффициентов

—число приведенных коэффициентов больше числа структурных коэффициентов

Модель сверхидентифицируема, если:

—число коэффициентов структурной модели равно числу коэффициентов приведенной формы модели

—число приведенных коэффициентов меньше числа структурных коэффициентов

+—число приведенных коэффициентов больше числа структурных коэффициентов

Модель считается идентифицируемой, если:

+—каждое уравнение системы идентифицируемо

—хотя бы два уравнения модели идентифицируемы

—большинство уравнений модели идентифицируемо

Необходимое условие идентификации выполняется, если для уравнения модели соблюдается счетное правило:

+—

— <

— >

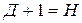
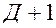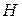
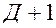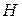
Структурные коэффициенты модели можно оценить тогда, когда:

—модель идентифицируема

—модель сверхидентифицируема

+—модель идентифицируема или сверхидентифицируема

Методы оценивания коэффициентов структурной модели:

—косвенный МНК

—двухшаговый и трехшаговый МНК

—метод максимального правдоподобия

+—косвенный МНК, двухшаговый и трехшаговый МНК, метод максимального правдоподобия

Под системой или моделью одновременных уравнений понимается:

+—случай, когда зависимая переменная в одном или нескольких уравнениях является объясняющей переменной в других уравнениях системы

—система из нескольких независимых уравнений, описывающих изучаемое явление

—система уравнений с одной и той и той же зависимой переменной, но с разным набором объясняющих переменных

Эндогенные переменные это:

+—зависимые переменные в системе одновременных уравнений, определяемые данной системой, даже если они появляются в качестве объясняющих переменных в других уравнениях системы

—переменные определяемые внешними факторами

—переменные в каждом уравнении, некоррелированные с соответствующей ошибкой

Предопределенные переменные включают в себя:

—экзогенные переменные, определенные внешними для данной модели факторами

+—экзогенные переменные и лаговые эндогенные переменные

—эндогенные переменные

Под смещением одновременных уравнений понимается:

+—переоценка или недооценка структурных параметров при применении структурных параметров при применении обычного МНК к структурным уравнениям модели одновременных уравнений

—результат, получаемый при использовании косвенного МНК

—оценка, получаемая при применении обычного МНК к приведенным моделям

Уравнения приведенной формы получаются:

+—путем решения структурных уравнений, когда каждая эндогенная переменная в системе выражается как функция только экзогенных или предопределенных переменных системы

—при решении структурных уравнений обычным МНК

—при уменьшении количества независимых переменных

Дана следующая система из двух структурных уравнений – простейшая модель спроса и предложения:

Спрос: 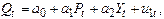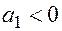и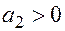

Предложение: , ,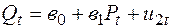

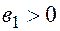где, 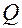- количество продаваемых и покупаемых товаров, 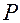- цена, 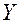- доход потребителей

Почему оценка данной функции спроса и предложения обычным МНК дает смещенные и несостоятельные оценки?

+—так как эндогенная переменная P является объясняющей переменной в обоих уравнениях и коррелирован с 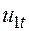в уравнении спроса и с 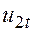в уравнении предложения

—так как для решения системы одновременных нельзя использовать МНК

—так как при решении системы одновременных уравнений невозможно получить несмещенные и состоятельные оценки

Дана следующая система из трех уравнений:

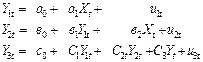
Может ли быть использован обычный МНК для оценки каждого из этих уравнений?

—нет

—только для первого

—только для второго и третьего

+—да, для каждого уравнения

Под идентификацией понимается:

+—возможность или невозможность получения структурных параметров системы одновременных уравнений через приведенные формы уравнений

—определение количества эндогенных переменных в системе уравнений

—получение оценок параметров приведенных уравнений

Дана следующая модель спроса и предложения:

Спрос: , ;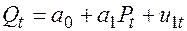

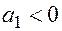Предложение: , :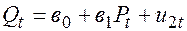

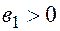—данная модель точно идентифицируема

—данная модель сверхидентифицируема

+—данная модель неидентифицируема

Косвенный МНК используется для определения состоятельных структурных параметров в системе одновременных уравнений:

+—если уравнения точно идентифицированы

—если уравнения неидентифицированы

—если уравнения сверхидентифицированы

Для точно идентифицированных уравнений двухшаговый метод наименьших квадратов дает оценки:

+—одинаковые с косвенным МНК

—лучше чем косвенный МНК

—хуже чем косвенный МНК

Дана следующая модель:

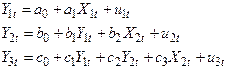
Данная модель является:

+—системой рекурсивных уравнений

—системой независимых уравнений

—системой взаимосвязанных моделей

Выберите верное из следующих утверждений: «Преимуществом двухшагового МНК, по сравнению с косвенным МНК, является то, что он может быть использован для получения состоятельных оценок структурных параметров…»:

+—…как для сверхидентифицированных, так и для точно идентифицированных уравнений в системе одновременных уравнений

—…для неидентифицированных уравнений в системе одновременных уравнений

—…как для неидентифицированных, так и для точно идентифицированных уравнений в системе уравнений

В правой части структурной формы взаимозависимой системы могут стоять:

—только экзогенные лаговые переменные

—только экзогенные переменные (как лаговые, так и нелаговые)

—только эндогенные лаговые переменные

—только эндогенные переменные (как лаговые, так и нелаговые)

+—любые экзогенные и эндогенные переменные