Системы линейных уравнений. Метод Крамера

Рассмотрим систему 3-х уравнений с тремя неизвестными

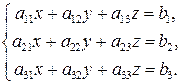(1.3)

Используя определители 3-го порядка, решение такой системы можно записать в таком виде:

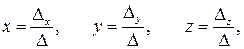(1.4)

если D¹0. Здесь

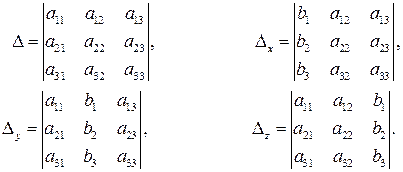(1.5)

Это есть формулы Крамера решения системы трех линейных уравнений с тремя неизвестными.

Пример 1.6. Решить систему линейных уравнений методом Крамера:

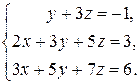
Решение. Находим определитель основной матрицы системы:

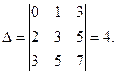
Поскольку D¹0, то для нахождения решения системы можно применить метод Крамера. Вычислим остальные определители:

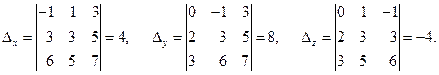
Тогда

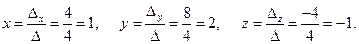
Проверка:

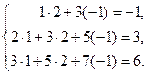
Следовательно, решение найдено правильно.

Теорема Крамера. Квадратная система линейных неоднородных уравнений n-го порядка с отличным от нуля определителем основной матрицы системы (D¹0) имеет одно и только одно решение, и это решение вычисляется по формулам:

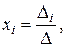
где D – определитель основной матрицы, D_i – определитель матрицы, полученной из основной, заменой i-го столбца столбцом свободных членов.

Отметим, что если D=0, то правило Крамера не применимо. Это означает, что система либо вообще не имеет решений, либо имеет бесконечное множество решений.

Матричный метод. Обратная матрица

Матрица А^–1 называется обратной матрицей по отношению к матрице А, если выполняется равенство AA^–1 = A^–1A = E. Только квадратные матрицы могут иметь обратные. Однако не каждая квадратная матрица имеет обратную. Для того чтобы матрица А имела обратную, необходимо и достаточно, чтобы ее определитель был отличен от нуля: detA¹0.

Пример 1.7. Решить систему линейных уравнений матричным методом (при помощи обратной матрицы).

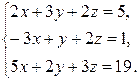
Решение. Запишем исходную систему уравнений в матричном виде:

.

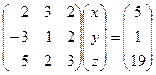Тогда решение можно формально записать в виде:

.

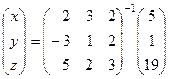Таким образом, чтобы найти решение системы, нужно вычислить обратную матрицу

.

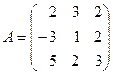Найдем ее

1) Вычисляем определитель исходной матрицы: .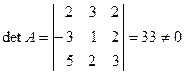

2) Транспонируем матрицу .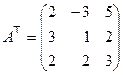

3) Находим все алгебраические дополнения транспонированной матрицы:

,	,	,
,	,	,
,	,	.

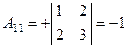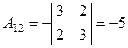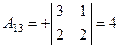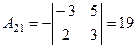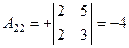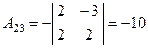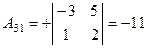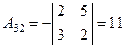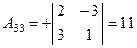4) Составляем присоединенную матрицу, для этого вместо элементов транспонированной матрицы ставим найденные алгебраические дополнения:

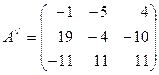
5) Записываем обратную матрицу, для этого все элементы присоединенной матрицы делим на определитель исходной матрицы:

.

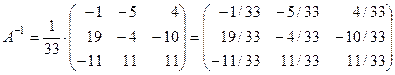6) Сделаем проверку:

.

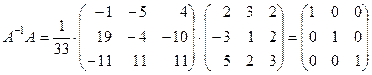Следовательно, обратная матрица найдена правильно.

Теперь, используя найденную обратную матрицу можно найти решение исходной системы:

.

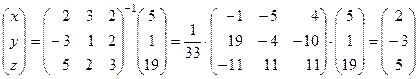Метод Гаусса

Рассмотрим произвольную систему линейных уравнений

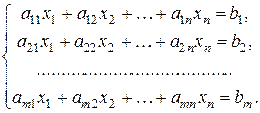(1.5)

В общем случае n¹m.

Задача теории систем линейных уравнений состоит в том, чтобы найти все решения системы. При этом возможны три случая. 1) Система вообще не имеет решений. Системы линейных уравнений, не имеющие ни одного решения, называются несовместными. 2) Система имеет хотя бы одно решение. такие системы называются совместными. 3) Система имеет только одно решение. Такие системы называются определёнными.

Метод Гаусса (метод последовательного исключения неизвестных) заключается в том, что с помощью элементарных преобразований система приводится к эквивалентной системе ступенчатого вида. Рассмотрим метод Гаусса на конкретных примерах.

Пример 1.8.Решить систему линейных уравнений методом Гаусса.

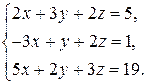
Решение. Выпишем расширенную матрицу системы, а затем при помощи элементарных преобразований строк приведем ее к треугольному виду:

.

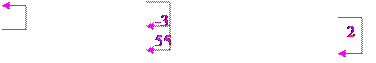
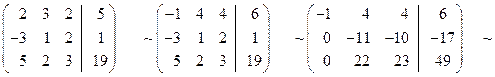
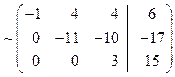Теперь выписываем соответствующую укороченную систему уравнений. Из последнего уравнения находим значение z и подставляем его во второе уравнение. После этого из второго уравнения находим y. Найденные значения y и z подставляем в первое уравнение, из которого затем находим значение x:

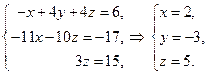
Эта тройка чисел будет являться единственным решением системы.

Пример 1.9. Решить систему методом Гаусса:

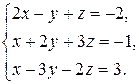
Решение. Выписываем и преобразуем расширенную матрицу системы

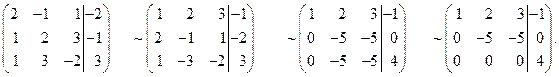
Записываем упрощенную систему уравнений:

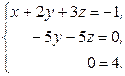
Здесь, в последнем уравнении получилось, что 0=4, т.е. противоречие. Следовательно, система не имеет решения, т.е. она несовместна.

Пример 1.10.Найти общее решение методом Гаусса

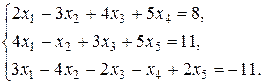
Решение. Выпишем расширенную матрицу системы, а затем при помощи элементарных преобразований строк приведем ее трапециевидной форме:

-1

:15

.

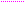
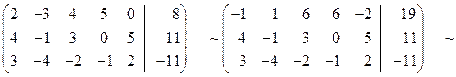
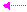
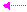
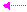
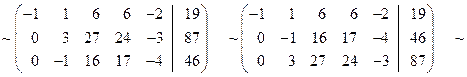
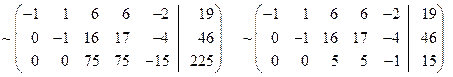Теперь выписываем соответствующую укороченную систему уравнений:

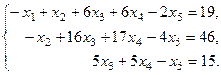
Пусть переменные x₄ и x₅ будут свободными, тогда переменные x₁, x₂ и x₃ будут основными (или базисными). Их мы оставим в левой части:

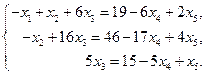
Разрешая эту систему относительно x₁, x₂ и x₃ получим

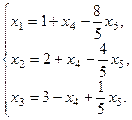
Это есть общее решение системы. Запишем это решение в параметрическом виде. Пусть x₄=a и x₅=5b. Тогда общее решение системы запишется в виде:

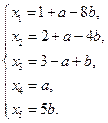
Давая числам a и b различные значения, будем получать частные решения. Например, если a=0, b=1, то x₁=–7, x₂=–2, x₃=4, x₄=0, x₅=5.

Ранг матрицы

Минором M_k k-го порядка матрицы А называется определитель k-го порядка с элементами, лежащими на пересечении любых k строк и k столбцов матрицы А. В частности, минорами 1-го порядка являются сами элементы матрицы А. В матрице А минор порядка r называется базисным, если он отличен от нуля, а все миноры большего порядка равны нулю или вообще не существуют. Отметим, что в матрице может быть несколько базисных миноров, но порядок у них будет одинаковым.

Рангом матрицы А называется наивысший порядок отличных от нуля миноров этой матрицы. Обозначать ранг матрицы А будем символом RgA. Матрицам с нулевым рангом соответствуют нулевые матрицы.

Пример 1.11.Вычислить ранг матрицы: а) методом окаймляющих миноров; б) методом элементарных преобразований:

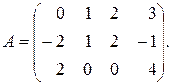
Решение. а) Фиксируем минор 2-го порядка, неравный нулю:

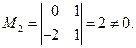
Вычисляем миноры 3-го порядка, окаймляющих М₂:

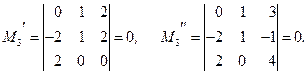
Следовательно, RgA=2, а минор М₂ – один из базисных миноров.

б) При помощи элементарных преобразований данной матрицы приведем ее к диагональному виду:

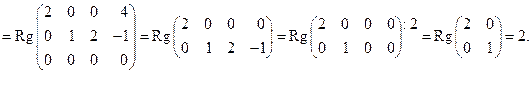
ВЕКТОРНАЯ АЛГЕБРА