А. Линейная алгебра и аналитическая геометрия
Семестр
1. Дать определение матрицы размера m×n.
2. Дайте определения квадратной, треугольной, диагональной и единичной матриц.
3. Какие матрицы называются равными?
4. Опишите операцию умножения матрицы на число.
5. Опишите операцию сложения матриц.
6. Опишите операцию умножения матриц.
7. Опишите операцию транспонирования матрицы.
8. Дайте определение перестановки и инверсии в ней. Как подсчитать число инверсий в перестановке (α1, α2, … αn)?
9. Для каких матриц вводится понятие определителя?
10. Опишите, как составляются слагаемые, входящие в определитель порядка n.
11. Дайте определение определителя порядка n.
12. Опишите правило вычисления определителя порядка 2.
13. Опишите правило вычисления определителя порядка 3.
14. Как изменится определитель при транспонировании матрицы?
15. Чему равен определитель, имеющий стоку или столбец, целиком состоящий из нулей?
16. Как изменится определитель, если его строку или столбец умножить на число α?
17. Как изменится определитель, если в нем переставить две строки или два столбца?
18. Опишите, в чем заключается линейное свойство определителя.
19. Как изменится определитель, если к какой-либо его строке прибавить другую, умноженную на некоторое число?
20. Как изменится определитель, если к какой-либо строке, умноженной на число α, добавить другую строку, умноженную на число β?
21. Чему равен определитель, имеющий две пропорциональные строки?
22. Как связаны между собой определители матриц А и λА?
23. Чему равен определитель произведения матриц А и В?
24. Дайте определение алгебраического дополнения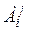 
элемента 
.
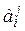25. Сформулируйте две теоремы об алгебраических дополнениях.
26. Дайте определение минора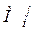 
.
27. Сформулируйте теорему о связи минора и алгебраического дополнения.
28. Опишите, как свести вычисление определителя порядка n к вычислению определителя порядка n-1.
29. Дайте определение обратной матрицы.
30. Какие матрицы имеют обратную?
31. Как найти элемент 
обратной матрицы?
32. Как найти матрицу Х из уравнения А·Х=В, если detА≠0?
33. Как найти матрицу Х из уравнения Х·А=В, если detА≠0?
34. Объясните, как понимаете слова: «Определена внутренняя операция над элементами множества А».
35. Объясните, как понимаете слова: «Определена внешняя операция над элементами множества А».
36. Сформулируйте аксиомы, характеризующие внутреннюю операцию в определении линейного пространства.
37. Сформулируйте аксиомы, характеризующие внешнюю операцию в определении линейного пространства.
38. Сформулируйте аксиомы, связывающие внешнюю и внутреннюю операции в определении линейного пространства.
39. Дайте определение понятий линейной комбинации, линейно зависимой и линейно независимой систем векторов.
40. Сформулируйте теорему о необходимом и достаточном условии линейной зависимости системы векторов.
41. Приведите примеры линейных пространств.
42. Какое линейное пространство называется n-мерным?
43. Дайте определение базиса n-мерного линейного пространства.
44. Сформулируйте теорему о разложении вектора по базису в n-мерном линейном пространстве.
45. Дать определение координат вектора в линейном пространстве.
46. Сформулируйте теорему о сведении внутренней и внешней операций над векторами к операциям над их координатами.
47. Дайте определение минора порядка m матрицы А.
48. Дайте определение ранга матрицы.
49. Дайте определение базисного минора, базисных строк и столбцов матрицы.
50. Сформулируйте теорему о базисном миноре.
51. Сформулируйте правило, позволяющее определить линейно зависимые строки (столбцы) матрицы или нет.
52. Сформулируйте правило, позволяющее определить, является ли данная строка матрицы линейной комбинацией других строк или нет.
53. Сформулируйте теорему о необходимых и достаточных условиях равенства нулю определителя.
54. Определите преобразования матрицы, называемые элементарными.
55. Опишите практический способ отыскания ранга матрицы.
56. Какие два линейных пространства называются изоморфными?
57. Дайте определение подпространства. Понятие линейной оболочки.
58. Сформулируйте теорему о размерности линейной оболочки L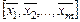 
.
59. Какое линейное пространство называется евклидовым?
60. Запишите неравенство Коши - Буняковского.
61. Какие два вектора из Еn называются ортогональными?
62. Дайте определение ортогональной системы векторов в Еn. Сформулируйте теорему о линейной независимости ортогональной системы.
63. Опишите процесс ортогонализации системы векторов из Еn.
64. Как строится матрица перехода от одного базиса к другому?
65. Запишите формулы, связывающие координаты одного и того же вектора в двух базисах (в матричной форме).
66. Укажите свойства матрицы перехода от одного ортонормированного базиса к другому.
67. Запишите формулы, связывающие координаты одного и того же вектора в двух ортонормированных базисах.
68. Какие формы записи систем линейных уравнений знаете? Запишите систему, используя правило Эйнштейна, а также в матричной форме.
69. Дайте определение решения системы.
70. Дайте определения совместных, несовместных, определенных и неопределенных систем.
71. Сформулируйте теорему о совместности произвольной системы линейных уравнений.
72. Какие две системы называются эквивалентными?
73. Для каких систем линейных уравнений применимо правило Крамера? Запишите формулы Крамера.
74. Как узнать, какие из уравнений можно удалить из системы, не нарушая ее эквивалентности?
75. Какие неизвестные системы называют свободными, а какие – зависимыми?
76. Дайте определение общего и частного решений системы.
77. Сформулируйте две теоремы о существовании нетривиальных решений однородной системы.
78. Свойства решений системы линейных однородных уравнений.
79. Из каких свойств решений линейной однородной системы следует, что множество всех решений таких систем образует линейное пространство? Какова его размерность?
80. Дайте определение фундаментальной системы решений однородной системы линейных уравнений. Сколько решений содержит Ф.С.Р.?
81. Дайте определение геометрического вектора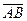 
, его модуля | 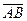| и нулевого вектора. Какие два вектора называются коллинеарными?
82. Какие два вектора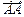 
и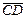 
называются равными?
83. Как отложить вектор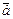 
от точки А?
84. Как определяется операция сложения векторов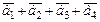 
?
85. Как определяется операция умножения вектора на число?
86. Дать определение понятий: «Линейная комбинация геометрических векторов», «Линейно зависимые и линейно независимые системы векторов».
87. Понятие аффинного и декартова базиса во множестве геометрических векторов. Понятие координат вектора. Как устроен базис на прямой, плоскости и в пространстве?
88. Что означает геометрически линейная зависимость системы двух векторов?
89. Какая система векторов называется компланарной? Что означает геометрически линейная зависимость системы из трех и более векторов?
90. Понятие аффинной и декартовой систем координат. Как называют оси в декартовой системе координат?
91. Понятие радиуса-вектора точки и координат точки. Как найти координаты вектора, зная координаты его конца и начала?
92. Как понимаете утверждение: «Точка М делит отрезок АВ в отношении λ.
93. Запишите координаты точки М, делящей отрезок АВ в отношении λ, если А(х1,у1), В(х2,у2).
94. Понятие проекции точки на ось и проекции вектора на ось. Чему равна проекция вектора 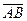на ось 
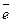, если ( 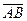^ 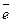)=φ?
95. Дайте определение скалярного произведения геометрических векторов. Его свойства.
96. Как узнать, используя скалярное произведение, какой угол (прямой, тупой или острый) образуют векторы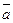 
и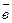 
?
97. Запишите формулы вычисления скалярного произведения ( 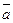, 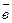) если известны декартовы координаты векторов 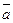и ?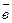
98. Как, используя понятие скалярного произведения, найти длину вектора и расстояние между двумя точками?
99. Как найти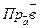 
, cos ( ^ )?
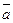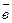100. Дайте определение направляющих косинусов вектора. Как их найти?
101. Понятие орта вектора. Как найти координаты орта вектора?
102. Понятие правой и левой связки двух векторов. Понятие левой и правой тройки векторов.
103. Дать определение векторного произведения геометрических векторов 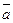и .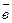
104. Свойства векторного произведения.
105. Геометрический смысл |[ , ]|.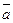
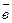106. Формула вычисления векторного произведения, если известны декартовы координаты векторов.
107. Дать определения смешанного произведения трех векторов.
108. Геометрический смысл |( , ,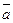 
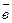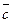)| и знака ( , , ).
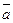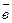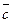109. Как узнать компланарна тройка векторов 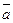, , 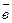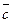или нет, используя понятие смешанного произведения?
110. Формула вычисления смешанного произведения векторов по их известным декартовым координатам.
111. Понятие функции f: х Í Rn→y Í Rm.
112. Определение линейного оператора А: Rn→Rm.
113. Как строится матрица линейного оператора А: Rn→Rm?
114. Как найти координаты вектора А[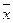 
], зная матрицу оператора А: Rn→Rm?
115. Запишите матрицу линейного оператора А: R1→R1.
116. Запишите матрицу линейного оператора А: Rn→R1.
117. Запишите матрицу линейного оператора А: R1→Rn.
118. Определите операцию сложения двух линейных операторов. Как найти матрицу суммы двух операторов?
119. Определите операцию умножения оператора на число.
120. Определите композицию двух линейных операторов. Как найти матрицу композиции линейных операторов А и В?
121. Понятие обратного линейного оператора.
122. Запишите закон изменения матрицы линейного оператора А: Rn→ Rn при переходе к новому базису.
123. Дать определение собственных чисел и собственного вектора линейного оператора
А: Rn→Rn.
124. Запишите характеристическое уравнение матрицы А.
125. Опишите процесс отыскания собственных векторов матрицы А.
126. Сформулируйте теорему о линейной комбинации собственных векторов, отвечающих одному и тому же собственному числу.
127. Сформулируйте теорему о системе собственных векторов, отвечающих попарно различным собственным числам.
128. Дайте определение уравнения плоской кривой L относительно декартовой системы координат.
129. Запишите уравнение окружности с центром в точке (х0,у0) радиуса R.
130. Дайте определение уравнения поверхности S относительно декартовой системы координат.
131. Дайте определение сферы. Запишите уравнение сферы с центром в точке, М0(х0,у0,z0) радиуса R.
132. Укажите способы задания кривой в пространстве.
133. Охарактеризуйте поверхности, задаваемые уравнениями F(x,y)=0, F(x,z)=0, F(y,z)=0.
134. Охарактеризуйте поверхность, задаваемую однородным уравнением F(x,y,z)=0. Объясните, какое уравнение называется однородным.
135. Охарактеризуйте поверхности, задаваемые уравнениями типа F(x,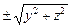 
)=0, F(y, 
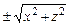)=0, F(z, 
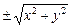)=0.
136. Опишите полярную систему координат. Запишите формулы, связывающие декартовы и полярные координаты точки.
137. Запишите в векторной и координатной форме уравнения прямой проходящей через точку М0(х0,у0) перпендикулярно вектору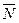 
=(А,В).
138. Запишите общее уравнение прямой на плоскости в декартовой системе координат. Охарактеризуйте его коэффициенты.
139. Охарактеризуйте прямые на плоскости, задаваемые неполными уравнениями Вх+D=0, Ау+D=0, Ах+Ву=0, х=0, у=0.
140. Запишите параметрические и канонические уравнения прямой на плоскости.
141. Запишите формулу вычисления расстояния от точки М0(х0,у0) до прямой Ах+Ву+С=0 на плоскости.
142. Запишите уравнение прямой с угловым коэффициентом, охарактеризуйте его коэффициенты.
143. Запишите формулы для вычисления угла между прямыми.
144. Как охарактеризовать взаимное расположение двух прямых А1х+В1у+С1=0, А2х+В2у+С2=0?
145. Запишите в векторной и координатной форме уравнения плоскости, проходящей через точку М0(х0,у0,z0) перпендикулярно вектору 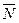={А,В,С}.
146. Запишите общее уравнение плоскости. Охарактеризуйте его коэффициенты.
147. Запишите в векторной и координатной форме уравнения плоскости, проходящей через точку М0(х0,у0,z0) с радиусом вектором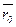 
параллельно векторам 
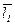={m1,n1,p1} и 
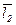={m2,n2,p2}.
148. Запишите формулу вычисления расстояния от точки М0(х0,у0,z0) до плоскости Ах+Ву+Сz+D=0.
149. Как найти угол между двумя плоскостями А1х+В1у+С1z+D1=0 и А2х+В2у+С2z+D2=0?
150. Как охарактеризовать взаимное расположение трех плоскостей по заданным общим уравнениям?
151. Запишите параметрические и канонические уравнения прямой в пространстве.
152. Запишите общее уравнение прямой в пространстве.
153. Опишите процесс перехода от общих уравнений прямых в пространстве к каноническим и параметрическим.
154. Запишите в векторной форме формулу вычисления расстояния от точки до прямой в пространстве.
155. Запишите в векторной форме формулу для вычисления расстояния между двумя прямыми в пространстве.
156. Как охарактеризовать взаимное расположение двух прямых в пространстве?
157. Дайте определение эллипса.
158. Запишите каноническое уравнение эллипса. Объясните выбор декартовой системы координат. Изобразите эллипс на рисунке.
159. Дайте определение эксцентриситета эллипса и его директрис.
160. Дайте определение гиперболы.
161. Запишите каноническое уравнение гиперболы. Изобразите гиперболу на рисунке.
162. Дайте определение эксцентриситета гиперболы и его директрис.
163. Дайте определение параболы.
164. Запишите каноническое уравнение параболы. Изобразите параболу на рисунке.
165. Опишите процесс приведения к каноническому виду общего уравнения а11х2+2а12ху+а22у2+а1х+а2у+b=0 кривой второго порядка.
166. – 187. Укажите название, изобразите на рисунке поверхность, уравнение которой в декартовой системе координат может быть записана в виде:
179. 
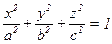
180. 
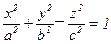
181. 
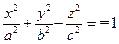
182. 
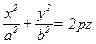(p>0)
183. 
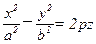(p>0)
184. 
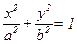
185. 
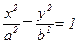
186. 
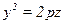
187. 
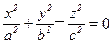
188. Опишите процесс приведения общего уравнения второго порядка а11х2+а22у2+а33z2+2а12ху+2а13хz+2а23уz+а1х+а2у+а3z+b=0 к каноническому виду.
В. Математический анализ
1. Опишите понятие множества. Приведите примеры множеств. Поясните смысл утверждения: «Множество А задано». Какие способы задания множеств знаете.
2. Объясните, что означают следующие записи аÎА, аÏА, АÍВ, ВÍА.
3. Какие два множества называются равными. Как можно доказать, что А=В.
4. Дайте определение объединения суммы двух множеств. Приведите примеры.
5. Дайте определение пересечения двух множеств. Приведите примеры.
6. Понятие разности двух множеств.
7. Понятие универсального множества. Понятие дополнения множеств.
8. Дайте определение действительного числа. Какие числа называются рациональными, иррациональными.
9. Дайте определение модуля действительного числа, укажите его свойства.
10. Запишите в виде неравенств множества действительных чисел: [а,b], (a,b), [a,b), (a,b].
11–15. Дайте определения и приведите примеры:
11) верхней границы множества А;
12) точной верхней границы множества А;
13) нижней границы множества А;
14) точной нижней границы множества А;
15) ограниченного сверху (снизу), ограниченного множества.
16. В чем заключается свойство непрерывности, плотности и упорядоченности множества действительных чисел.
17. Символы -¥, +¥, ¥. Запишите в виде неравенств множества [а,+¥), (а,+¥], (-¥,а], (-¥,а).
18. Операции с символами -¥, +¥, ¥.
19. Понятие функции f: хÍRn→yÍRm.
20. Понятие области определения и области значений функции.
21. Охарактеризуйте частные классы функций f: хÍRn→yÍRm при различных значениях m и n. Примеры таких классов.
22. Понятие графика функции.
23–28. Дать определение и привести примеры следующих классов функций f: хÍR→yÍR:
23) монотонно убывающей, строго монотонно убывающей функции;
24) монотонно возрастающей, строго монотонно возрастающей функции;
25) четной, нечетной функций и функции общего вида;
26) ограниченной сверху (снизу), ограниченной функции;
27) неограниченной сверху (снизу), неограниченной функции;
28) периодической функции.
29. Опишите класс основных элементарных функций. Укажите их область определения и область значений. Постройте график каждой из основных элементарных функций.
30. Дайте определение композиции функций.
31. Понятие обратной функции.
32. Виды окрестностей конечной точки х0 на прямой, их обозначения и запись в виде неравенств.
33. Понятия односторонней окрестности точки х0 на прямой. Их обозначения и запись в виде неравенств.
34. Понятия шаровых и параллелепипедальных окрестностей на плоскости и в пространстве.
35. Окрестности -¥, +¥, ¥ на прямой, их обозначение и запись в виде неравенств.
36. Понятие предельной точки, внутренней и граничной точки множества. Понятие границы множества, открытые и замкнутые множества.
37–60. Дать определение на языке окрестностей и неравенств, привести рисунок для понятий:
37) 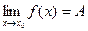 | 38) 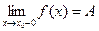 | 39) 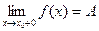 | 40) 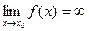 | 41)  |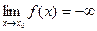
42) 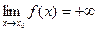 | 43) 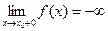 | 44) 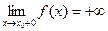 | 45) 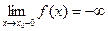 | 46)  |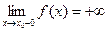
47) 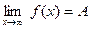 | 48) 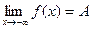 | 49) 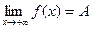 | 50) 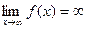 | 51)  |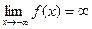
52) 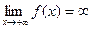 | 53) 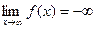 | 54) 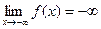 | 55) 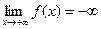 | 56)  |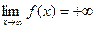
57) 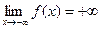 | 58) 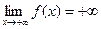 | 59) 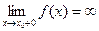 | 60)  |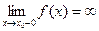
61. Понятие числовой последовательности. Виды числовых последовательностей.
62. Понятие предела числовой последовательности.
63. Понятие векторной последовательности.
64. Сформулировать теорему о пределе векторной последовательности.
65. Сформулировать теорему о пределе монотонной ограниченной последовательности.
66. Дать определение предела функции на языке последовательностей.
67. Сформулировать и доказать теорему об единственности предела.
68. Сформулировать и доказать теорему об ограниченности функции, имеющей конечный предел.
69. Сформулировать и доказать теорему о пределе суммы, произведения и частного.
70. Сформулировать и доказать теорему о переходе к пределу в неравенстве f(x)< j(х)< y(х) .
71. Сформулировать и доказать теорему о переходе к пределу в неравенстве f(x)£ b.
72. Сформулировать теорему о пределе при М®М0 функции f: хÍRn→yÍRm.
73. Сформулировать теорему о связи пределов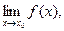 
.
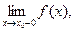
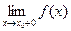74. Сформулировать теорему о связи пределов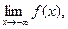 
.
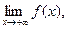
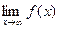75. Сформулируйте различные определения непрерывности функции в точке х0.
76. Сформулировать и доказать теорему о непрерывности сложной функции.
77. Понятие непрерывности функции слева и справа.
78. Теорема о непрерывности суммы, произведения и частного функции.
79. Сформулировать теорему Коши о промежуточных значениях непрерывной на [a,b] функции.
80. Сформулируйте первую теорему Вейерштрасса об ограниченности непрерывной на [a,b] функции.
81. Как Вы понимаете слова: функция на [a,b] достигает своего наименьшего и наибольшего значений? Сформулируйте вторую теорему Вейерштрасса.
82. Запишите и докажите справедливость первого замечательного предела и некоторых его следствий.
83. Приведите различные формы записи второго замечательного предела. Докажите, что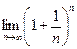 
существует.
84. Запишите следствия второго замечательного предела и докажите их.
85. Приведите классификацию разрывов функции: f: хÍR→yÍR.
86. Понятие бесконечно малой и бесконечно большой функции. Примеры.
87. Сформулировать и доказать теорему о связи бесконечно малой и бесконечно большой функции.
88. Сформулировать и доказать теорему о произведении бесконечно малой и ограниченной функций.
89. Сформулировать и доказать теорему о разности функции и ее предела.
90. Дайте определение порядка малости бесконечно малой функции a(х) относительно b(х).
91. Понятие эквивалентности двух бесконечно малых функций.
92. Понятие главной части бесконечно малой функции относительно другой бесконечно малой.
93. Сформулируйте и докажите свойства эквивалентных бесконечно малых.
94. Объясните, как можно применять понятие эквивалентных бесконечно малых при отыскании пределов.
95. Как определяют бесконечно малые и бесконечно большие функции в случае f: хÌRn→yÍRm?
96. Дайте определение дифференцируемой функции. Понятие производной матрицы и дифференциала.
97. Сформулируйте и докажите теорему о связи дифференцируемости и непрерывности.
98. Строение производной матрицы в случае f: хÍR→yÍR.
99. Строение производной матрицы в случае f: хÌRn→yÌR. Понятие частных производных.
100. Строение производной матрицы в случае f: хÍR→yÍRn и . f: хÍRm→yÍRn
101. Получите формулы для производных всех основных элементарных функций.
102. Сформулируйте правила дифференцирования суммы, произведения и частного.
103. Сформулируйте и докажите теорему о дифференцировании сложной функции.
104. Укажите формулу дифференцирования функции U= f [x1(t), x2(t),…,xn(t)].
105. Укажите правило дифференцирования функции U= f [x1(t1, t2, …,tn), x2(t1, t2, …,tn),…,
xn(t1, t2, …,tn)].
106. Опишите правило дифференцирования обратных функций.
107. Понятие производной по направлению.
108. Запишите и докажите формулу вычисления производной по направлению. Понятие градиента.
109. Понятие производных высших порядков от f: хÌR→yÌR.
110. Понятие частных производных высших порядков.
111. Сформулируйте теорему о равенстве смешанных частных производных.
112. Опишите правило дифференцирования параметрически заданных функций. Объясните параметрический способ задания функций.
113. Поясните неявный способ задания функций f: хÌR→yÌR. Правило их дифференцирования.
114. Правило отыскания частных производных функций, заданных неявно.
115. Геометрический и механический смысл производной функции f: хÌR→yÌR.
116. Записать уравнение касательной к кривой при различных способах ее задания.
117. Уравнение касательной плоскости и нормали к поверхности.
118. Как записать дифференциал для функции f: хÍR→yÍR?
119. Как записать дифференциал для функции f: хÍRn→yÍR?
120. Как записать дифференциал для функции f: хÍR→yÍRn?
121. Как записать дифференциал для функции f: хÍRn→yÍRm?
122. В чем заключается свойство инвариантности формы записи первого дифференциала?
123. Как определяются дифференциалы d2f, d3f,…, dnf ?
124. Записать общий вид дифференциалов d2f, d3f,…, dnf для функций f: хÌR→yÌR, если х – независимая переменная.
125. Записать выражение для d2f функции у = f(х), если х = х(t).
126. Записать выражение для d2f функции z = f(х,y).
127. Записать выражение для d3f функции z = f(х,y).
128. Запишите формулу Тэйлора порядка n для функций у = f(х), у = f(х1, x2,…, xn) в дифференциальной форме.
129. Запишите формулу Тэйлора порядка n для функций у = f(х), используя в записи производные.
130. Записать формулу Маклорена для функций ex, sin x, cos x, ln(1+x), (1+x)a.
131. Сформулируйте и докажите теорему о поведении функции f(х) в окрестности точки х0, если f’(х) > 0, (f’(х) < 0).
132. Сформулируйте и докажите теорему Ферма об обращении в нуль производной в точке наибольшего (наименьшего) значения.
133. Сформулируйте и докажите теорему Ролля об обращении производной в нуль.
134. Сформулируйте и докажите теорему Лагранжа (об отношении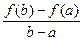 
).
135. Сформулируйте и докажите теорему Коши (об отношении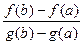 
).
136. Сформулируйте и докажите теорему о дифференцируемости функции f: хÌR→yÌR.
137. Сформулируйте и докажите теорему о дифференцируемости функции f: хÌRn→yÌR.
138. Сформулируйте правило Лопиталя раскрытия неопределенности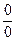 
139. Сформулируйте правило Лопиталя раскрытия неопределенности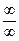 
140. Как раскрыть неопределенность 0×¥, ¥-¥?
141. Как раскрыть неопределенность 00, 1¥, ¥0?
142. Дайте определение точек экстремума для функции у = f(х), у = f(х1, x2,…, xn).
143. Сформулируйте и докажите необходимое условие экстремума для функций у = f(х) и
у = f(х1, x2,…, xn).
144. Сформулируйте и докажите достаточные условия экстремума для функций f(х), связанные со знаком f’(х).
145. Сформулируйте и докажите достаточные условия экстремума для функций f(х), связанные со второй производной и производной порядка n.
146. Положительно и отрицательно определенные квадратичные формы. Сформулируйте критерий Сильвестра положительно и отрицательно определенной квадратичной формы.
147. Сформулируйте достаточные условия экстремума функций f(х1, x2,…, xn).
148. Опишите правило отыскания наибольшего и наименьшего значений функции на замкнутом множестве.
149. Понятие условного экстремума.
150. Какие знаете способы отыскания условного экстремума?
151. Дайте определение выпуклости вверх и вниз графика функции.
152. Сформулируйте необходимые и достаточные условия выпуклости вниз (вверх) графика функции, связанные со второй производной.
153. Понятие точки перегиба и правило их отыскания.
154. Понятие асимптоты графика функции.
155. Как найти вертикальные асимптоты?
156. Как найти горизонтальные асимптоты?
157. Как найти наклонные асимптоты?
158. Опишите схему исследования и построения графика функции.