Радианная мера углов и дуг

Вопросы для проверки

1. Что такое числовая окружность?

2. Перечислите признаки числовой окружности.

3. Какая величина принимается за единицу измерения при градусном измерении углов?

4. Что такое радиан?

5. По каким формулам переводят градусную меру угла в радианную и наоборот?

6. Выразите в радианах углы, равные 30°, 45°, 60°, 90°, 180°, 270°, 360°.

7. Почему ошибочна запись p = 180°?

8. При каком условии длина дуги равна ее радианной мере?

9. Какой угол называется углом поворота?

10. Какой угол поворота называется положительным? отрицательным?

11. Задайте формулой общий вид углов поворота.

12. Сформулируйте правило «полного оборота».

13. Какие функции называются тригонометрическими?

14. Дайте определение функции синус; косинус; тангенс; котангенс.

15. При каких углах не определен тангенс? котангенс?

16. Назовите значения тригонометрических функций углов 30°, 45°, 60°.

17. Какие значения может принимать синус? косинус? тангенс? котангенс?

18. Определите знаки тригонометрических функций в зависимости от того, в какой четверти находится аргумент.

19. Какие из тригонометрических функций являются четными, какие – нечетными?

20. Чему равен период синуса? косинуса? тангенса? котангенса?

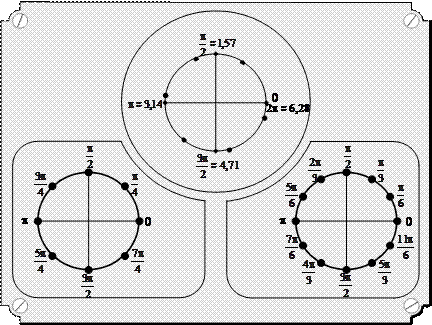
Числовая окружность

Единичная окружность — это окружность, радиус которой принят за единицу измерения.

Числовая окружность — это единичная окружность с установленным соответствием между действительными числами и точками окружности:

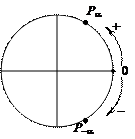
Указанное соответствие можно определить следующим образом: каждому числу a соответствует такая точка Р числовой окружности, чтобы дуга ÈОР имела длину |a| и была отложена в положительном направлении если a > 0 и в отрицательном, если a < 0:

Признаки числовой окружности:

1) начало отсчета – правый конец горизонтального диаметра;

2) единичный отрезок – длина радиуса окружности;

3) положительное направление – против часовой стрелки.

Откладывать можно дуги какой угодно длины. То есть числовую окружность можно рассматривать как окружность радиуса 1, на которую «намотана» числовая прямая:

Радианная мера углов и дуг

Угол в 1° — это центральный угол, опирающийся на дугу, длина которой равна части окружности.

Угол поворота — это угол, полученный вращением луча около его начала О от начального положения ОА до конечного положения ОВ.

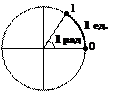Угол в 1 радиан — это центральный угол, опирающийся на дугу, длина которой равна радиусу окружности.

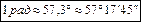
Радианная мера угла численно равна пути, который проходит точка по дуге единичной окружности, на которую опирается этот угол:

Для связи радианов и градусов используют развернутый угол:

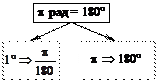1. Говорят: «угол радиан» или чаще «угол ». Обозначение «радиан» или «рад», как правило, опускают.

2. Термин «радианное измерение углов» равносилен термину «числовое измерение углов», т.е. фраза «угол a равен двум радианам» равносильна фразе «угол a равен числу 2» и даже «угол a равен двум». Поэтому вопрос типа «Чему равно ?» некорректен. Нужно спрашивать: «Чему равен угол ?» (60°) или «Чему равно число ?» (» 1,05).

Угол поворота

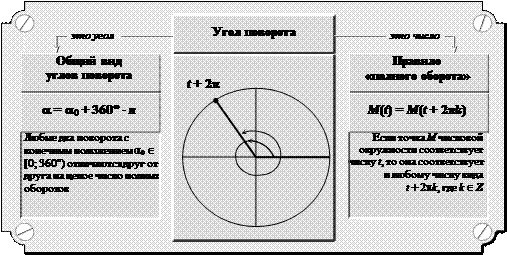áПолныйñ оборот — это угол поворота, равный 2p рад (или 360°).

Некоторые положения конечной точки угла поворота: