Счетные и несчетные множества

Для того, чтобы сравнить два каких-либо множества А и В, между их элементами устанавливают соответствие.

Если это соответствие взаимнооднозначное, то множества называются эквивалентными или равномощными, А ~ В или А Û В.

Примеры:

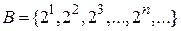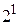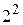1. Множества А = {1, 2, 3, …, n, …} и являются равномощными, т. к. между их элементами можно установить взаимнооднозначное соответствие: 1 « , 2 « , 3 « 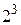, …, n « , ….

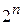2. Множество точек катета BC и гипотенузы AC треугольника ABC являются равномощными (рис. 1).

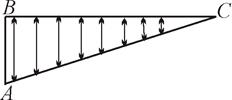
Рис. 1

3. Можно установить взаимнооднозначное соответствие между точками отрезка [0; 1] и множеством точек всей числовой прямой (-∞; +∞). Построим полуокружность радиуса r = 0,5 с центром в точке С (0,5; 0,5) (рис. 2).

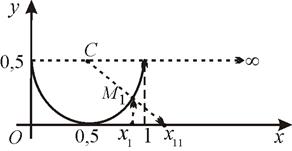
Рис. 2

Через точку 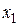, принадлежащую отрезку [0; 1], проведем прямую параллельно оси Oy до пересечения с полуокружностью в точке 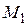. Через точки С и 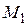проведем прямую до пересечения с осью Ox в точке 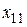. Следовательно, точке 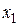соответствует точка 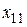и наоборот. Таким образом, можно установить соответствие между любой точкой отрезка [0; 1] и точкой множества точек числовой прямой (-∞; +∞). В частности, если 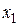= 0,5, то 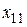= 0,5; если 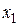= 1, то 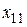= ¥. Следовательно, эти множества равномощные, [0; 1] ~ (-∞; ∞).

Последовательностью называется множество чисел, перенумерованных с помощью натуральных чисел и расставленных в порядке возрастания их номеров .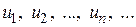

Счетным множеством называется множество эквивалентное множеству натуральных чисел.

Следовательно, любая последовательность является счетным множеством.

Предложение 1. Для того, чтобы множество было счетным, необходимо и достаточно, чтобы его можно было представить в виде последовательности.

Предложение 2. Декартово произведение конечного или счетного числа счетных множеств является счетным множеством.

Предложение 3. Любое подмножество счетного множества является либо конечным, либо счетным.

Таким образом, счетное множество является наименее мощным из бесконечных множеств.

Более мощным, чем счетное множество, является множество действительных чисел 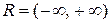. Его мощность называют мощностью континуума. Так как [0; 1] ~ R, то множество точек отрезка [0; 1] обладает также мощностью континуума.

Функции, их классификация

Одним из основных понятий математического анализа является функция.

Зачатки определения функции имелись у П. Ферма и Б. Паскаля. Впервые слово функция употребил Лейбниц в 1692 г.

Определение функции, наиболее близкое к современному, дал И. Бернулли в 1718 г.

До недавнего времени наиболее распространенным было следующее определение функции.

Переменная величина y называется функцией переменной величины x,если каждому значению х соответствует единственное определенное значение y. Записывается .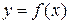

В настоящее время обычно употребляют определение функции, основанное на теории множеств.

Переменная величина y называется функцией переменной величины x с областью определения D и множеством значений E, если для любого значения х, принадлежащего множеству D (" x Î D)существует единственное значение y, принадлежащее множеству Е (y Î E) (рис. 3), т. е.

.

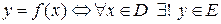Рис. 3

Например, найти область определения и множество значений функции 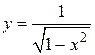. Получаем , .

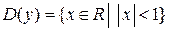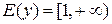Если между множествами D и E можно установить взаимно однозначное соответствие, то существует обратная функция 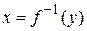или .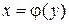

Если аргумент функции 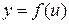является в свою очередь функцией переменной величины х 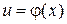, то 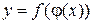называется сложной функцией.

Здесь функци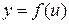и и 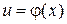называются составляющими функциями.

Например, 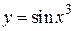сложная функция, ее составляющие функци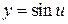и и .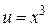

Основными элементарнымифункциями являются следующие:

1) 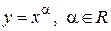- степенная функция;

2) 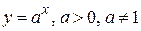- показательная функция;

3) 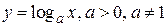- логарифмическая функция;

4) 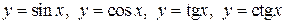- тригонометрические функции;

5) 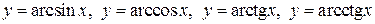- обратные тригонометрические функции.

Функция называется элементарной, если она образована из основных элементарных с помощью конечного числа алгебраических действий: сложения, вычитания, умножения, деления, возведения в рациональную степень.

Например, .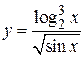

Функция называется алгебраической, если она образована из независимой переменной x с помощью конечного числа алгебраических действий: сложения, вычитания, умножения, деления, возведение в степень с рациональным показателем.

Функция называется трансцендентной, если она не является алгебраической.

Алгебраическая функция называется иррациональной, если она содержит операцию извлечение корня.

Функция называется рациональной, если она является алгебраической и не содержит корней независимой переменной.

Простейшей рациональной функцией является многочлен вида

,

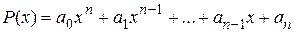где 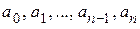– числовые коэффициенты, х – независимая переменная, n – целое положительное число.

Любую рациональную функцию можно представить в виде отношения двух многочленов

,

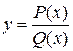где 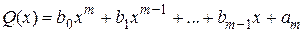, 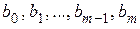– числовые коэффициенты, m – целое положительное число.

Предел последовательности

Окрестностью точки 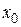называется любой интервал, содержащий эту точку.

d-окрестностью точки 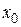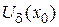называется интервал длиной 2d с центром в этой точке.

В математическом анализе обычно рассматривается d-окрестность точки 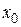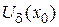, которая не содержит точку 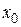(рис. 4).

Кратко записывается

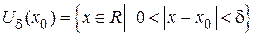
или .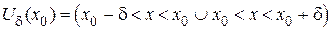

Рис. 4

Пусть в некоторой области D имеется предельная точка .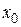

Точка называется предельной, если любая, сколь угодно малая, ее окрестность содержит бесконечное множество точек этого множества. Из любого бесконечного множества точек можно выбрать бесконечное счетное множество, т.е. последовательность 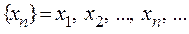. Пусть эта последовательность такая, что с увеличением номера n члены последовательности 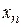неограниченно приближаются к 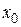, но никогда не достигают его. Так что расстояние от точки х до точки 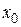становится сколь угодно мало, но никогда не становится равным нулю. В этом случае говорят, что члены последовательности 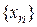стремятся к 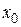. Стремятся к 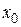– значит неограниченно приближаются, но не достигают 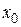(рис. 5).

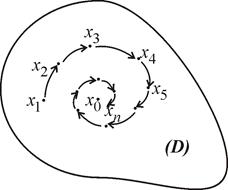
Рис. 5

Определение предела последовательности. Число b называется пределом последовательности 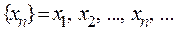( 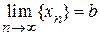), если для любого, сколь угодно малого, положительного d существует такое положительное число N, что если номер члена последовательности n > N, то 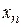принадлежит d-окрестности числа b ( 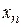Î ).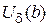

Кратко с помощью кванторов можно записать

.

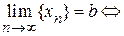
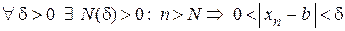Например, доказать, что 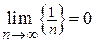. Запишем последнее соотношение из определения предела и преобразуем его, учитывая, что 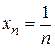, а b = 0. Получим 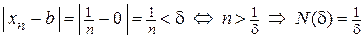. Отсюда следует, что для того, чтобы член последовательности 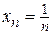отличался от предела b = 0 меньше, чем на d = 0,001, его номер n должен быть больше 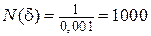(n > 1000). При d = 0,0001 N(d) равняется 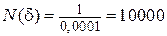и т. д. Таким образом, для любого d можно выбрать N(d) такое, что 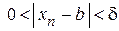, если только n > N(d). Следовательно, предел этой последовательности равен нулю.

Теорема Больцано-Коши (без доказательства). Для того, чтобы последовательность 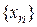имела предел, необходимо и достаточно, чтобы для любого d > 0 существовало N(d)> 0 такое, что если n > N, m > N, то .

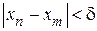Теорема Вейерштрасса (без доказательства). Если последовательность монотонно возрастает (убывает) и ограничена сверху (снизу), то она имеет предел.

Последовательность 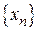называется монотонно возрастающей (убывающей), если для любого n Î N ( ).

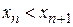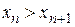Предел функции