Принцип наложения. Метод наложения

Принцип (теорема) наложения гласит, что ток в любой ветви (напряжение на любом элементе) сложной схемы, содержащей несколько источников, равен алгебраической сумме частичных токов (напряжений), возникающих в этой ветви (на этом элементе) от независи­мого действия каждого источника в от­дельности.

Для упрощения доказательства теоремы выберем одну из наружных вет­вей сложной схемы за номером 1, в которой действительный ток равен контур­ному: I₁ = I_k1. Составим для сложной схемы систему контурных уравнений 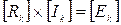и решим ее относительно тока I₁ = I_k1 методом определителей (Крамера):

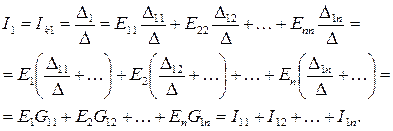
Здесь G₁₁ –входная проводимость ветви 1, G₁₂, G₁₃, …, G_1n– взаимные проводимости между 1-й и остальными ветвями, I₁₁ = E₁G₁₁ – частичный ток в ветви 1 от источника ЭДС E₁, I₁₂ = E₂G_{12, …,} I_1n = E_nG_1n – частичные токи в ветви 1 от источников ЭДС E₂,…, E_n.

Принцип наложения выполняется только для тех физических величин, которые опи­сываются линейными алгебраическими уравнениями, например, для токов и напряжений в линейных цепях. Принцип наложения не выполня­ется для мощности, которая с током связана нелинейным уравнением P=I²×R.

Принцип наложения лежит в основе метода расчета сложных цепей, по­лучившего на­звание метода наложения. Сущность этого метода состоит в том, что в сложной схеме с не­сколькими источниками последовательно рассчиты­ваются частичные токи от каждого источ­ника в отдельности. Расчет частичных токов выполняют, как правило, методом преобразова­ния схемы. Действитель­ные токи определяются путем алгебраического сложения частичных токов с учетом их направлений.

E1 E2

Пример.Задана схема цепи (рис. 21) и параметры ее элементов:E₁ =12 B; E₂ =9 B; R₁= R₂ =R₃ = 2 Ом. Требуется определить токи в ветвях схемы методом наложения.

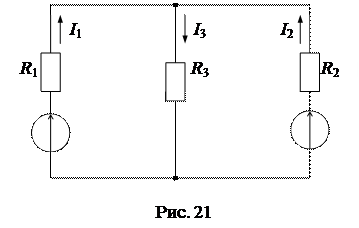
На рис. 22а представлена схема цепи для определения частичных токов от источника ЭДС Е₁, а на рис. 22б - от источника ЭДС Е₂.

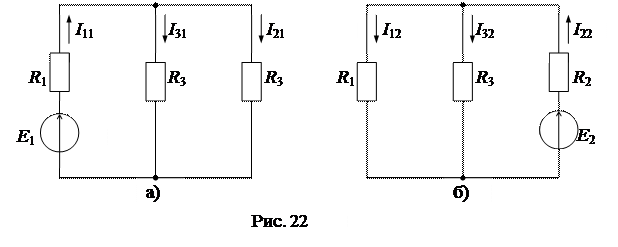Частичные токи в схеме рис. 22а от E₁:

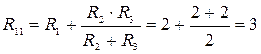Ом; I₁₁= E₁/R₁₁=12/3 = 4A; I₂₁= I₃₁= 2А.

Частичные токи в схеме рис. 22б от E₂:

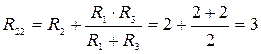Ом; I₂₂ = E₂/R₂₂ = 9/3 = 3A; I₁₂= I₃₂ = 1,5А.

Действительные токи как алгебраические суммы частичных токов:

I₁ = I₁₁ - I₁₂ = 4 – 1,5 = 2,5 A

I₂ = - I₂₁ + I₂₂ = -2 + 3 =1 A

I₃ = I₃₁+ I₃₂ = 2 + 1,5 =3,5 A

Теорема о взаимности

Выделим из сложной схемы две произвольные ветви “m” и “n”, в одной из которых включен источник ЭДС E (в ветви m). Теорема о взаимности гласит, что если источник ЭДС E, включенный в ветви “m”, вызывает в ветви “n” час­тичный ток I , то такой же источник ЭДС E, включенный в ветвь “n”, вызовет в ветви “m” такой же частичный ток I (рис.23) .

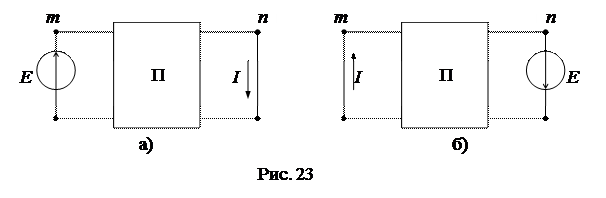Доказательство теоремы о взаимности вытекает из принципа наложения. Частичные токи равны:

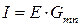— для схемы рис. 23а, 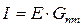— для схемы рис. 23б.

Так как взаимные проводимости в линейной цепи равны (G_mn=G_nm), то соответственно равны токи в обеих схемах.

Теорема о компенсации

Формулировка теоремы: любой пассивный элемент электрической схемы можно заменить а) идеальным источником напряжения с ЭДС, равной напряжению на этом элементе (E=U) и направленной навстречу току, б) иде­альным источником тока J, равным току в этом элементе (J=I) и направленным согласно току I.

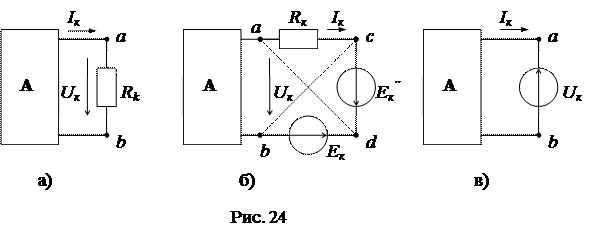Выделим пассивный элемент R_k с током I_k и напряжением U_k из схемы цепи (рис. 24а). Для доказательства п. а) теоремы включим последовательно с элементом R_k навстречу друг другу два идеальных источника ЭДС 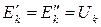(рис. 24б). Такое включение источников ЭДС не вызовет изменения режима сложной схемы, так как их действие взаимно компенсируется. Cоставим потен­циальное уравнение между точками “a” и “d” :

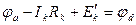, откуда следует 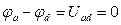, или .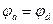

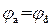Точки “a” и “d”, как точки равного потенциала, можно закоротить и за­короченный участок “a-d” из схемы удалить без нарушения ее режима. В ре­зультате удаления закороченного участка схема получает вид рис. 24в, в кото­рой пассивный элемент R_k заменен идеальным источником ЭДС .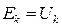

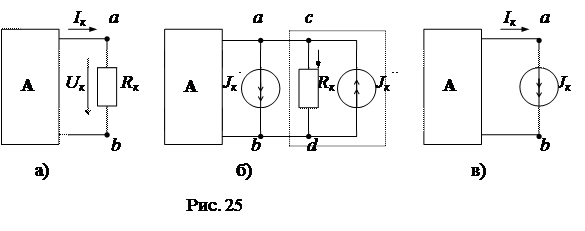Для доказательства п. б) теоремы включим параллельно с элементом R_k два идеальных источника тока 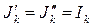, направленные навстречу друг другу (рис. 25б).

Такое включение источников тока 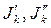не вызовет изменения режима сложной схемы, так как их действия взаимно компенсируются. С другой сто­роны ток в ветви “a-c” равен нулю ( 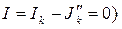, и эту ветвь можно отклю­чить без нарушения режима остальной части схемы. В результате отключения схема получает вид рис. 25в, в которой пассивный элемент R_k заменен идеаль­ным источником тока J_k=I_k .