Таким образом, в цикле Kapно сумма приведенных теплот равна нулю

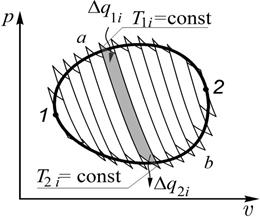Рис. 3.8

Рассмотрим далее произвольный обратимый цикл. Его можно представить как совокупность весьма большого числа элементарных циклов Карно, состоящих каждый из двух адиабат и двух бесконечно малых изотерм, как показано на рис. 3.8. По каждой из изотерм на участке 1-2 происходит подвод весьма малого (элементарного) количества теплоты 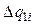при соответствующей температуре 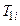. А на участке 2-1 - отвод теплоты 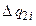при температуре 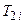.Осуществление такого произвольного обратимого цикла потребует наличия большого количества теплоотдатчиков и теплоприемников с различными температурами. Видно, что рассматриваемая совокупность элементарных циклов Карно (при увеличении их числа до бесконечности) эквивалентна исходному произвольному циклу. Действительно, суммарная площадь всех таких циклов Карно равна площади данного цикла. Следовательно, эквивалентная этой площади работа данного цикла и работа совокупности элементарных циклов Карно будут также одинаковы. Суммарное количество подведенной теплоты будет равно 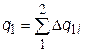и при устремлении числа элементарных циклов к бесконечности станет точно равным подведенному количеству теплоты в данном цикле. То же можно сказать и об отведенной теплоте .

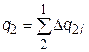Для каждого из этих элементарных циклов Карно сумма приведенных теплот равна нулю, т.е.

.

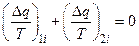Тогда, просуммировав такие равенства, записанные для каждого из этих циклов Карно, получим

,

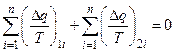где n - число таких циклов Карно, или (при n ® ¥)

,

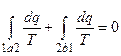то есть 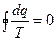, (3.7)

где символ 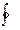обозначает интеграл, взятый по всему замкнутому контуру рассматриваемого цикла.

Таким образом, в произвольном обратимом цикле интегральная сумма элементарных приведенных теплот равна нулю.

Рассмотрим теперь необратимые циклы. Во всяком необратимом цикле, осуществляемом с тем же теплоотдатчиком (с температурой Т₁) и тем же теплоприемником (с температурой Т₂), что и цикл Карно, термический КПД (вследствие неравновесности процессов и диссипации энергии) будет меньше, чем у цикла Карно:

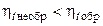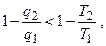или откуда 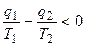, т.е. .

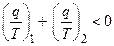Следовательно, в произвольном необратимом цикле сумма приведенных теплот отрицательна.

Тогда, повторяя вывод, приведенный выше для произвольного обратимого цикла, можно показать, что для произвольного необратимого цикла

, (3.8)

т.е. в произвольном необратимом цикле интегральная сумма элементарных приведенных теплот отрицательна.

Объединяя формулы (3.7) и (3.8), в общем случае будем иметь

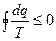, (3.9)

где знак равенства относится к обратимым циклам, а знак неравенства - к необратимым. Формула (3.9) называется неравенством Клаузиуса.

Энтропия и ее свойства

Энтропией называется термодинамическая функция, полный дифференциал которой ,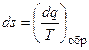

где 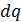– тепло, подведенное к газу в обратимом процессе. Размерность энтропии Дж/(кг∙К).

3.7.1. Свойства энтропии в обратимых процессах

1. Для кругового обратимого процесса из неравенства Клазиуса следует, что 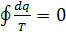или .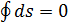

2. Изменение энтропии 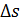в любом обратимом процессе перехода вещества из состояния 1 в состояние 2 не зависит от пути этого процесса, а зависит только от параметров вещества в его начальном и конечном состояниях.

Докажем это, рассмотрев обратимый круговой процесс 1-а-2-b-1 (рис. 3.9), в котором некоторое тело (газ) сначала переходит из состояния 1 в

состояние 2 по пути 1-а-2, а потом возвращается в состояние 1 по пути 2-b-1. Согласно неравенству Клаузиуса, в этом случае

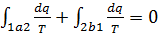или .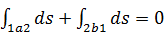

Теперь рассмотрим такой же процесс, но с переходом из состояния 1 в состояние 2 по другомупути 1-с-2 (см. рис. 3.9) . В этом случае также

или .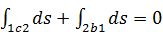

Сравнивая эти равенства, видим, что

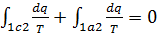или .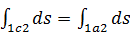

Таким образом, энтропия является функцией состояния вещества, а её величина однозначно определяется параметрами его состояния в начале и конце процесса.

3. Энтропия термодинамической системы, состоящей из нескольких частей (энтропии которых равны S₁, S₂,..., S_n), равна сумме энтропий всех её частей:

.

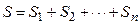4. Энтропия отдельного тела или системы тел в различных обратимых процессах может как возрастать, так и уменьшаться. Действительно, из определения энтропии следует, что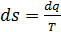

.

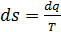Так как , а 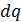может быть как положительным, так и отрицательным, то подводу теплоты соответствует 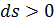, а отводу - .

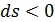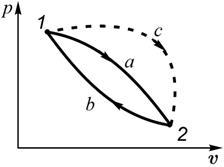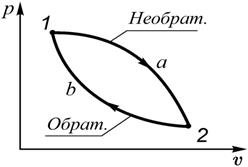Рис. 3.9	Рис. 3.10

3.7.2. Особенности изменения энтропии в необратимых процессах

Пусть рабочее тело переходит из состояния 1 в состояние 2 в необратимом процессе 1а2, а возвращается в исходное состояние в обратимом процессе 2б1 (рис. 3.10). Тогда цикл 1а2б1 является необратимым и для него справедливо неравенство Клазиуса 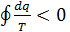или .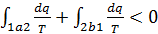

Но для обратимого процесса .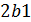

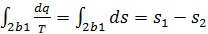Тогда для необратимого процесса 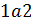получим .

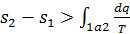Таким образом, в необратимых процессах изменение энтропии всегда больше интегральной суммы приведенных теплот данного процесса.

В дифференциальной форме последнее неравенство для необратимых процессов можно записать в виде .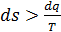

Это соотношение можно объединить с выражением для обратимых процессов, в которых .

Тогда в общем случае получим .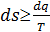

Знак 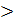относится к необратимым процессам, а знак равенства – к обратимым процессам.

Это выражение является аналитической записью второго закона термодинамики.