Производные высшего порядка

Пусть y = f(x) является дифференцируемой функцией. Тогда производная также представляет собой функцию от x. Если она является дифференцируемой функцией, то мы можем найти вторую производную функции f, которая обозначается в виде

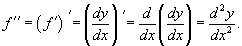
Аналогично, если f '' существует и дифференцируема, мы можем вычислить третью производнуюфункции f:

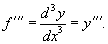
Производные более высокого порядка (если они существуют), определяются как

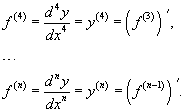
Примеры.

а) Найти производную сложной функции .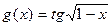

Решение.

Здесь мы имеем дело с композицией трех функций, из которых внешней является тангенс. Производная тангенса равна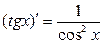

Тогда

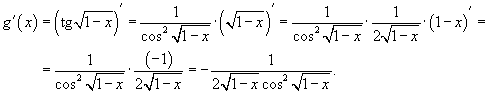
б) Продифференцировать функцию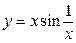

Решение.

Сначала найдем производную произведения:

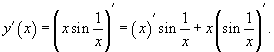
Далее, по формуле производной сложной функции

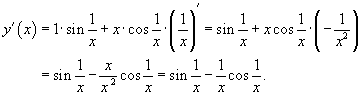
в) Определить производную функции .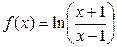

Решение.

Применим формулы производной сложной функции и производной частного.

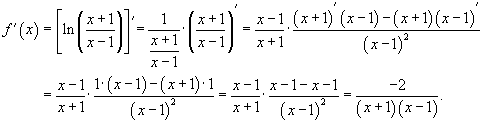
г) Найти y'', если .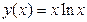

Решение.

Возьмем первую производную дифференцируя функцию как произведение.

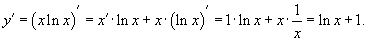
Теперь найдем производную второго порядка

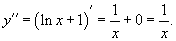
д) Вычислить производную степенно-показательной функции

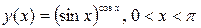
Решение.

Прологарифмируем заданную функцию:

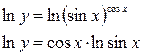
Вычислим производную, воспользовавшись формулой производной произведения и производной сложной функции:

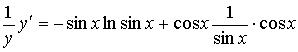
Выразим производную заданной функции:

.

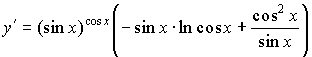е) Вычислить производную функции с помощью логарифмического дифференцирования

.

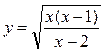Решение.

Прологарифмируем функцию:

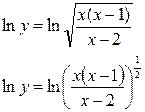
Преобразуем выражение с помощью свойств логарифмов:

;

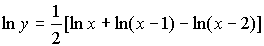Продифференцируем полученное равенство

.

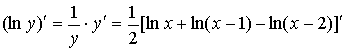
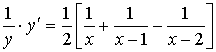Выразим производную заданной функции:

.
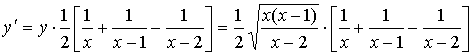