Занятие № 6. Метод итераций

Цель - ознакомить студентов с методом итераций решения алгебраических уравнений.

Если каким-либо способом получено приближенное значение x₀ корня уравнения f(x)=0, то уточнение корня можно осуществить методом последовательных приближений или методом итераций. Для этого уравнение

f(x)=0 представляют в виде

x = φ (x) (15)

что всегда можно сделать, и притом многими способами, например,

x = x + c • f(x) (16)

где с - произвольная постоянная.

Пусть число x₁ есть результат подстановки x₀ в правую часть уравнения (15), т.е. x₁=φ(x₀). Далее, x₂=φ(x₁), x₃=φ(x₂),...,

x_n+1=φ (x_n) (17)

Процесс последовательного вычисления чисел x_n (n=1,2,3,...). по формуле (17) называется методом последовательных приближений или методом итераций.

Утверждение. Итерационный процесс сходится 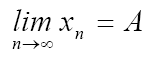(здесь А- точный корень исходного уравнения f(x)=0), если на отрезке [a,b] содержащем корень А и его последовательные приближения x_n, выполнено условие

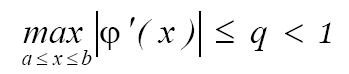(18)

Замечание. В качестве первого приближения x₀ можно взять произвольное значение из интервала, содержащего корень A, причем такой интервал можно сделать достаточно малым.

Для оценки погрешности метода итераций используется следующая формула

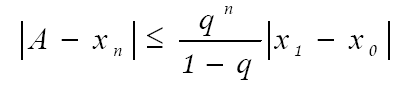(19)

При 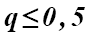оценка погрешности упрощается

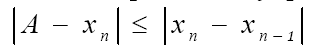(20)

Пример 1 . Методом итераций найти меньший положительный корень уравнения x³ -5x+1=0.

Решение. Графически отделяя корни данного уравнения, заключаем, что уравнение имеет три действительных корня, лежащих в отрезках [-3;-2], [0;1], [2;3]. Найдем корень принадлежащий отрезку [0; I]. Укажем отрезок меньшей длины, на котором находится корень. Поскольку, f(x)=x³ -5x+1, f(0)=1>0, 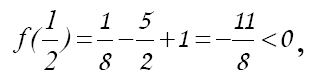, то корень принадлежит отрезку [0; 0,5]. Данное уравнение приведем к виду (15), разрешая его относительно x:

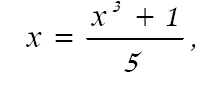т.е.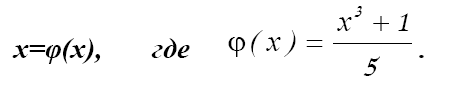

Так как, 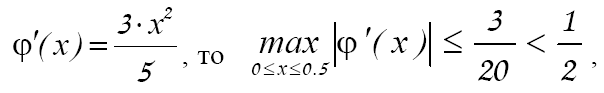то условие (18) выполняется, следовательно процесс итераций будет сходиться, а для оценки погрешности можно использовать (20).

Взяв в качестве начального приближения середину отрезка, т.е. приняв x₀=0,25, вычисление последующих приближений проведем по формуле

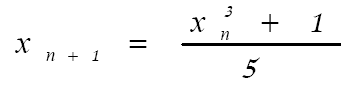
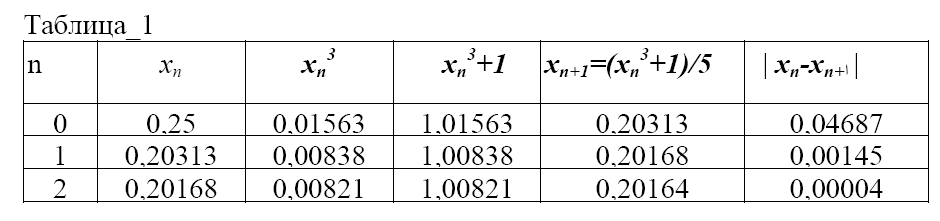
Результаты этих вычислений представлены в таблице_1, из которой видно, что искомый корень A= 0,20164, вычислен с заданной точностью ε=0,0001, т.к. согласно формуле (20) имеем

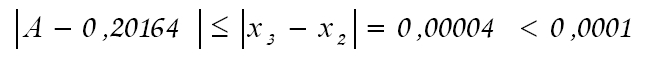
Замечание. При нахождении двух других корней исходного уравнения методом последовательных приближений уже нельзя пользоваться формулой

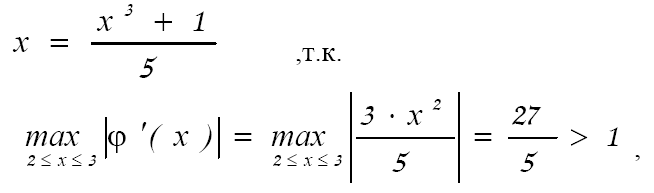
т.е. условие (18) не выполняется. В этом случае данное уравнение следует представить в другом виде, например, 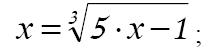для функции 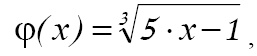условие (18) на отрезках [-3;-2], [2;3] будет выполняться.

Пример 2. Методом итераций найти отрицательный корень уравнения

x⁴ + x -3 = 0

Решение. Данное уравнение имеет два действительных корня; отрицательный корень находится на отрезке [-1,5;-1,4], так как для его концов выполняется условие

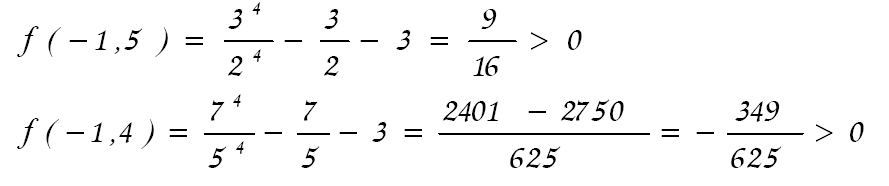
Уравнение запишем в виде (16):

x = x + c • ( x ⁴ + x — 3 )

где с - произвольная постоянная. Выберем значение с так, чтобы для функции 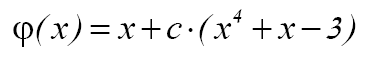на отрезке [-1,5;-1,4] выполнялось условие (18). В качестве такого значения можно взять с=0,1, тогда

φ (x) = x + 0,1 • (x⁴ + x — 3 ) ,

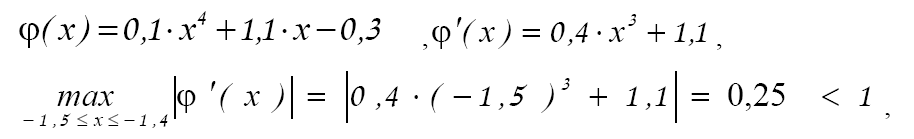
т.е. выполнено условие (18).

Возьмем x₀=-1,45. Вычисление последующих приближений осуществим по формуле

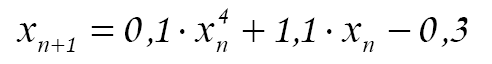
и представим результаты в таблице_2, из которой видно, что A=-1,45262 является приближенным корнем данного уравнения.

Таблица_2

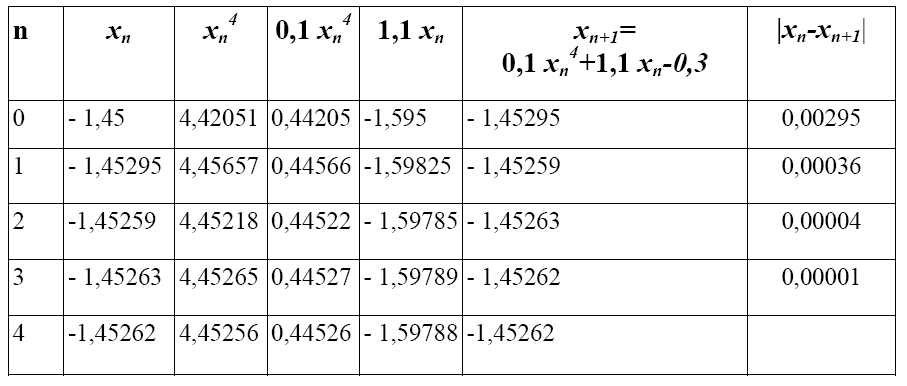
Задания: Выполнить задание 2.2 и 3 ИДЗ№1.