Если система (2.3) имеет единственное решение, определяемое по формулам:

2) Если ==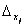0, система имеет бесконечно много решений.

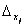
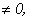3) Если =0, а хотя бы один из система не имеет решений.

Примеры:

1. Рассмотрим систему 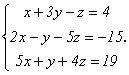, решенную в предыдущем разделе методом Гаусса, и применим к ней правило Крамера. Найдем все нужные определители:

следовательно, система имеет единственное решение.

Отсюда

2. 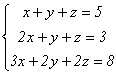. Здесь поскольку имеет два одинаковых столбца.

Следовательно, система не имеет единственного решения. Найдем и

поэтому система имеет бесконечно много решений.

3. 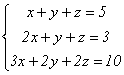. Для этой системы но

следовательно, решений нет.

Лекция 3.

Операции над матрицами, их свойства. Обратная матрица, ее вычисление.

Матричная запись системы линейных уравнений. Решение матричных уравнений и линейных систем с помощью обратной матрицы.

Определение 3.1. Матрицы одинаковой размерности называются равными, если у них соответственно равны элементы, стоящие на одинаковых местах.

Определение 3.2. Матрица называется нулевой, если все ее элементы равны 0.

Определение 3.3. Квадратная матрица называется единичной, если элементы, стоящие на ее главной диагонали, равны 1, а остальные равны 0.

Линейные операции над матрицами.

1. Сложение матриц.

Определение 3.4. Суммой матриц А и В одинаковой размерности mn называется матрица С той же размерности, каждый элемент которой равен сумме элементов матриц А и В, стоящих на тех же местах:

Свойства сложения:

1. А + В = В + А.

2. (А + В) + С = А + (В + С) .

3. Если О – нулевая матрица, то А + О = О + А = А

Замечание 1. Справедливость этих свойств следует из определения операции сложения матриц.

Замечание 2. Отметим еще раз, что складывать можно только матрицы одинаковой размерности.

Пример.

2. Умножение матрицы на число.

Определение 3.5. Произведением матрицы на число называется матрица той же размерности, что и исходная, все элементы которой равны элементам исходной матрицы, умноженным на данное число.

Свойства умножения матрицы на число:

1. (km)A=k(mA).

2. k(A + B) = kA + kB.

3. (k + m)A = kA + mA.

Замечание 1. Справедливость свойств следует из определений 3.4 и 3.5.

Замечание 2. Назовем разностью матриц А и В матрицу С, для которой С + В =А, т.е. С = А + (-1)В.

Пример.

. Тогда

Перемножение матриц.

Выше было указано, что сложение матриц накладывает условия на размерности слагаемых. Умножение матрицы на матрицу тоже требует выполнения определенных условий для размерностей сомножителей, а именно: число столбцов первого множителя должно равняться числу строк второго.

Определение 3.6. Произведением матрицы А размерности mp и матрицы В размерности называется матрица С размерности , каждый элемент которой определяется формулой: Таким образом, элемент представляет собой сумму произведений элементов i-й cтроки матрицы А на соответствующие элементы j-го столбца матрицы В.

Пример.

. При этом существует произведение АВ, но не существует произведение ВА. Размерность матрицы С=АВ составляет Найдем элементы матрицы С:

Итак,

Теорема 3.1 (без доказательства). Определитель произведения двух квадратных матриц равен произведению их определителей.

Замечание. Операция перемножения матриц некоммутативна, т.е. Действительно, если существует произведение АВ, то ВА может вообще не существовать из-за несовпадения размерностей (см. предыдущий пример). Если существуют и АВ, и ВА, то они могут иметь разные размерности (если ).

Для квадратных матриц одного порядка произведения АВ и ВА существуют и имеют одинаковую размерность, но их соответствующие элементы в общем случае не равны.

Однако в некоторых случаях произведения АВ и ВА совпадают.

Рассмотрим произведение квадратной матрицы А на единичную матрицу Е того же порядка:

Тот же результат получим и для произведения ЕА. Итак, для любой квадратной матрицы А АЕ = ЕА =А.

Обратная матрица.

Определение 3.7. Квадратная матрица А называется вырожденной, если , и невырожденной, если .

Определение 3.8. Квадратная матрица В называется обратной к квадратной матрице А того же порядка, если АВ = ВА = Е. При этом В обозначается .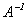

Рассмотрим условие существования матрицы, обратной к данной, и способ ее вычисления.

Теорема 3.2. Для существования обратной матрицы необходимо и достаточно, чтобы исходная матрица была невырожденной.

Доказательство.

1) Необходимость: так как то (теорема 3.1), поэтому

2) Достаточность: зададим матрицу 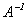в следующем виде:

Тогда любой элемент произведения (или ), не лежащий на главной диагонали, равен сумме произведений элементов одной строки (или столбца) матрицы А на алгебраические дополнения к элементам друго столбца и, следовательно, равен 0 (как определитель с двумя равными столбцами). Элементы, стоящие на главной диагонали, равны Таким образом,

=. Теорема доказана.

Замечание. Сформулируем еще раз способ вычисления обратной матрицы: ее элементами являются алгебраические дополнения к элементам транспонированной матрицы А, деленные на ее определитель.

Пример.

Найдем матрицу, обратную к

следовательно, матрица А невырожденная. Найдем алгебраические дополнения к ее элементам:

Не забудем, что алгебраические дополнения к элементам строки матрицы А образуют в обратной матрице столбец с тем же номером. Итак, Можно убедиться, что найденная матрица действительно удовлетворяет определению 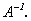Найдем