В недесяткових системах числення 2 страница
Як бачимо, у записаних числах, перша цифра одна й та сама, а друга у першому числі більша, ніж у другому, тому перше число більше від другого. Цей факт очевидний при записі натуральних чисел у десятковій системі числення.
3. Алгоритм переходу від десяткової системи числення до іншої позиційної системи з довільною основою q
Якщо дане число менше від основи системи числення, до якої треба перейти, то його так і записують. Наприклад у вісімковій системі числення числа 1, 2, 3, 4, 5, 6, 7 записують так само, як і в десятковій, - це однозначні числа. Число 9 записують вже так 11(8) , тобто одна вісімка і одна одиниця; 10 записують як 12(8). При великих числах усно важко виконати такий перехід. Використовують таке правило.
Правило.Щоб натуральне число, записане в десятковій системі, подати в позиційній системі при основі q, треба поділити це число на основу q; частку знову поділити на q і т. д. Одержані при цьому послідовні остачі будуть цифрами цього числа, записаними при основі q: перша остача – цифрою одиниць, друга остача – цифрою одиниць другого розряду (q), третя остача – цифрою одиниць третього розряду (q2) і т. д., остання остача – цифрою найвищого в цьому числі розряду.
Запишемо число 869 при основі q = 4. Виконаємо послідовні ділення.
869 4
868 217 4
1 216 54 4
1р. 1 52 13 4
ІІр. 2 12 3
ІІІр. 1
ІVр. Vр.
869 = 312114
4. Перехід від недесяткової системи числення до десяткової
1-й спосіб. Використовуємо основну формулу запису числа. Наприклад, запишемо число 364127 в десятковій системі:
364127 = 3 × 74 + 6 × 73 + 4 × 72 + 1 × 7 + 2 = 7203 + 2058 + 196 + 7 + 2 = 9466.
Алгоритм. Для того, щоб будь-яке число aq, де q ≠ 10, записати в десятковій системі числення, досить зобразити його у вигляді суми розрядних одиниць, усно виразити всі цифри і основу q у десятковій системі і виконати обчислення.
2-й спосіб. Щоб записати число аq в десятковій системі, треба одиниці вищого розряду помножити на основу системи, додати одиниці наступного розряду, одержаний результат помножити на основу системи і т. д., аж поки не додамо одиниці останнього розряду. Розв’яжемо попередній приклад цим способом.
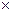
21+6=27
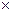
189+4=193
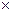
1351+1=1352
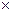
9464+2 =9466 Отже, 364127 = 9466
5. Перехід від однієї недесяткової системи числення
до іншої недесяткової системи числення
Для того, щоб перейти від однієї не десяткової системи числення до іншої, треба дане число аq записати в десятковій системі, а потім перевести його з десяткової системи в систему з основою p.
Наприклад, число 364127 записати в системі числення з основою 5. Для цього треба перетворити це число в десяткову систему числення: 364127 = 9466 (з попереднього прикладу), а потім 9466 записати в п’ятірковій системі числення:
9466 = 3003315. Таким чином, 364127=3003315.
6. Алгоритми додавання і віднімання, множення і ділення чисел
в недесяткових системах числення
Дії над числами в позиційній системі числення з основою р ≠ 10 виконуються за тими самими правилами, що й у десятковій системі числення. Для виконання додаваннятреба вміти додавати одноцифрові числа. Для цього слід складати таблиці додавання одноцифрових чисел. Таблиця додавання при р =5.
+ 1 2 3 4
1 2 3 4 10
2 3 4 10 11
3 4 10 11 12
4 10 11 12 13
Обчислимо суму 4342135+23435. Запишемо доданки один під одним:
4342135
+ 23435
4421115
Можна і не користуватися таблицею, а виконувати додавання розрядних одиниць в десятковій системі, а їхню суму для запису відразу переводити у відповідну систему. В даному разі 3+3=6, але у п’ятірковій системі 6 записується як 11- одна п’ятірка і одна одиниця (6 = 5+1).
Віднімання системних чисел виконується аналогічно додаванню. Якщо а>b, то а - b = (an – bn ) qn +(a n-1 – b n-1)q n-1 +…+(a1-b1)q+(a0-b0)
Якщо у якійсь із різниць виявиться, що ai<bi, то беремо одну одиницю наступного вищого розряду і роздроблюємо її в одиниці даного розряду, дістанемо q+ai і виконуємо віднімання:( q+ai) – bi. Якщо ж виявиться, що в сусідньому вищому розряді немає одиниць, беремо одиницю ще вищого розряду, вона має q одиниць попереднього нижчого розряду, в якому залишимо q-1 з цих одиниць, а одну роздробимо в одиниці потрібного нам ще нижчого сусіднього розряду і т. д. Наприклад:
3430016
- 242136
3143446
Міркуємо так: від одного відняти 3 не можна, але одиниць другого розряду у зменшуваному немає, одиниць третього розряду – теж. Беремо одну одиницю четвертого розряду. Вона має 6 одиниць третього розряду. У цьому розряді залишаємо 5 одиниць, а одну одиницю третього розряду роздроблюємо в одиниці другого розряду. Дістанемо 6 одиниць другого розряду, з них 5 залишимо в цьому розряді, а одну роздробимо в одиниці першого розряду, їх буде 6. Від 6 віднімемо 3 і додаємо 1 або до 6 додаємо 1 і потім віднімаємо 3, тобто: (6-3)+1 або (6+1)-3 і т. д.
Алгоритм множення цілих невід’ємних чисел в будь-якій системі числення з основою р такий же, як у десятковій системі числення. Як і при додаванні можна міркувати двома способами: множити одноцифрові числа в десятковій системі числення, а для запису кожний добуток переводити в систему числення з основою числення р, або ж скористатися таблицею множення в даній системі числення. Виконаємо множення у п’ятірковій системі числення:

 2435
2435
3215
+ 1041
1334
2001035
Виконати множення в трійковій системі числення: 2102 · 21; 122 · 22.
Виконати множення: 543216 ·236 (22222236); 3578 ·628 (282668); 1457 ·37 (5017)
(11) 1(13) ·1(12)(13) (183(12)13); 10102 ·1012 (1100102 ); 37819 ·239 (1003839).
Діленняв системах числення з основою, відмінною від 10, виконується так, як і в десятковій системі числення. Наприклад,
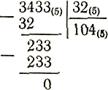
Оскільки дільник — двоцифрове число, то в діленому відокремлюємо дві цифри в найвищому розряді — 34; це число більше від 32. Тому при діленні першого числа на друге у частці маємо 1, а в остачі 2. Дописуємо до цієї остачі цифру 3. Число 23 менше від дільника, тому в частці одиниць другого розряду маємо 0. Дописуємо до 23 одиниць другого розряду 3 одиниці першого розряду, дістаємо число 233(5).
Це число більше від дільника і при діленні його на 32 дістаємо в частці 4 і в остачі 0.
Через те що правильність виконання дії ділення перевіряється за допомогою дії множення дільника і частки, то, застосовуючи правило знаходження числа цифр у добутку, можна сформулювати правило знаходження числа цифр у частці: кількість цифр у частці від ділення двох натуральних чисел дорівнює різниці цифр діленого і дільника або на одиницю більше.
РЕКОМЕНДОВАНА ЛІТЕРАТУРА
1. Курс математики: Навч. посібник / В. Н. Боровик. – К. : Вища шк., 1995. с. 141-142, 150-152.
2. Математика (практикум): Навч. посібник / В. М. Кухар. – К. : Вища шк., 1989. с. 229-232
3. Теоретичні основи початкового курсу математики: Навч. посібник / В. М. Кухар. – К. :вища шк., 1987. с. 199-206, 212-215.
4. Л. П. Стойлова. Основы начального курса математики.М. Просвещение. 1988. с. 166-176, 192-195
 Практичне заняття № 1
Практичне заняття № 1
Тема. Застосування усних і письмових прийомів додавання, віднімання, множення і ділення чисел. Виконання арифметичних дій в десятковій системі числення та інших системах числення, відмінних від десяткової.
Мета. Повторити алгоритми додавання, віднімання, множення і ділення чисел в десятковій системі числення та інших позиційних системах числення та застосувати їх до розв’язування вправ.
Студенти повинні знати:
· позиційні і непозиційні системи числення;
· способи переходу від однієї системи числення до іншої;
· представлення чисел в десятковій системі числення та інших не десяткових системах числення;
· алгоритми додавання та віднімання в десятковій системі числення, в інших позиційних системах числення;
· алгоритми множення та ділення в десятковій системі числення, в інших позиційних системах числення.
Студенти повинні вміти:
· записувати числа в різних системах числення;
· перетворювати числа з десяткової системи в не десяткову і навпаки;
· виконувати додавання, віднімання, множення та ділення чисел в десятковій системі числення та інших не десяткових системах числення;
· складати таблиці додавання, віднімання, множення і ділення чисел в різних системах числення.
Література
1. Курс математики: Навч. посібник / В. Н. Боровик. – К. : Вища шк., 1995. С. 112-116,143-155.
2. Теоретичні основи початкового курсу математики: Навч. посібник В. М. Кухар. – К. Вища шк., 1980. С. 166-177.
3. Теоретичні основи початкового курсу математики: Навч. посібник В. М. Кухар. – К. Вища шк., 1987. С. 169-177, 199-223.
4. Основы начального курса математики: Учеб. пособие Л.П. Стойлова. – М. “Просвещение”.1988. С. 128-137,169-197.
5. Математика. Множини. Логіка. Цілі числа: Практикум В. М. Кухар. – К. Вища шк., 1989. С. 170-175, 180-181, 229-261.
6. Сборник задач по математике: Учеб. Пособие А. М. Пышкало. – М. Просвещение., 1979. С. 163-174,180-181.
План та хід заняття
І. Актуалізація опорних знань
1. Що називається системою числення?
2. Який запис вважають десятковим розгорнутим записом?
3. Алгоритм переходу від десяткової системи числення до іншої позиційної системи з довільною основою q.
4. Алгоритм переходу від недесяткової системи числення до десяткової.
5. Як представити число в десятковій системі числення та інших недесяткових системах числення?
6. Алгоритми додавання та віднімання в десятковій системі числення, в інших позиційних системах числення.
7. Алгоритми множення та ділення в десятковій системі числення, в інших позиційних системах числення.
ІІ. Розв’язування вправ
1. Записати подані числа у вигляді суми розрядних одиниць: 254 624; 2791 345.
2. Запишіть числа 2458, 12435, 11 0012 у вигляді суми степенів основи системи числення.
3. Запишіть число 254 у системі числення з основою q = 5.
4. Запишіть число 32425 у десятковій системі числення.
5. На прикладі додавання чисел 237 і 526 покажіть, які теоретичні факти лежать в основі алгоритму додавання багатоцифрових чисел.
6. При вивчення алгоритму додавання трицифрових чисел в початковій школі послідовно розглядаються випадки додавання 231+342, 425+4+135, 237+526, 529+299. Які особливості додавання в кожному з них?
7. На прикладі віднімання чисел 875 і 528 покажіть, які теоретичні положення лежать в основі алгоритму віднімання багатоцифрових чисел.
8. На прикладах множення чисел 397 і 6 покажіть, які теоретичні відомості лежать в основі алгоритму множення трицифрового числа на одноцифрове.
9. Покажіть, що множення 524 на 168 зводиться до множення багатозначного числа на однозначне і складу багатозначних чисел, а потім знайдіть значення добутку цих чисел «стовпчиком».
10. Виконайте ділення кутиком:
1) 11455 : 145; 2) 261960 : 740; 3) 105754 : 253; 4) 213664 : 352.
11. При якому значенні q правильні рівності: 236q = 12405 , 5(14)5q = 134010?
12. Визначте, при якому значенні змінної має місце рівність:
а) 752x – 647x = 67; б) 35x + 40x = 115x ; в) 220 – 306x = 124x ;
г) 34 – 102x = 212x ; д) 626x : 123x = 5.
13. При якому значенні p виконуються рівності:
14. Записати число 254 у системі числення з основою q = 6.
15. Запишіть в десятковій системи числення число 1213.
16. Розв’язати рівняння х-432(6)=561(6) різними способами і подати результат у десятковій системі числення.
19. Виконайте дії: : 4413(6)-3243(6)+40432(6); 21(11)39(12)-37(10)4(12); 321(5)∙43(5);
20. Задача (загадкова біографія). У паперах одного дивака-математика знайдено його «біографію»:
«Я закінчив курс університету 44 років від роду. Через рік, 100-річним юнаком я одружився з 34-річною дівчиною. Незначна різниця у віці – всього 11 років – сприяла тому, що ми жили спільними інтересами і мріями. Незабаром у нас була вже сім’я із 10 чоловік» і т.д. У якій системі числення написано цю біографію?
21. Виконайте дії:
1) 4 (10) 5(13)∙(11) 2(13);2) 1101(2)∙101(2); 4) 101(2)∙111(2);
2) 221(3)∙12(3); 5) 10111(2)∙10011(2);
3) 343224(7)∙125(7); 6) 3411(5)∙421(5).
ІІІ. Самостійне виконання вправ
Варіант 1
1. Записати число 254 у системі числення з основою q = 6.
2. Запишіть в десятковій системи числення число 1213.
3. Записати число у вигляді суми розрядних одиниць 23 451.
4. При якому значенні q правильні рівності: 21q = 1510; 306q + 124q = 22010.
5. Виконати дії і результат подати в десятковій системі числення:
4523156 + 213445 – 101012.
Варіант 2
1. Записати число 844 у системі числення з основою q = 5.
2. Запишіть в десятковій системи числення число 2415.
3. Записати число у вигляді суми розрядних одиниць 59 455.
4. При якому значенні q правильні рівності: 203q = 5310; 102q + 212q = 3410.
5. Виконати дії і результат подати в десятковій системі числення:
2523456 + 213435 – 100112.
Варіант 3
1. Записати число 294 у системі числення з основою q = 4.
2. Запишіть в десятковій системи числення число 2213.
3. Записати число у вигляді суми розрядних одиниць 54 551.
4. При якому значенні q правильні рівності: 1000q = 2710; 752q - 647q = 6710.
5. Виконати дії і результат подати в десятковій системі числення:
2543156 + 213545 – 111012.
Варіант 4
1. Записати число 654 у системі числення з основою q = 3.
2. Запишіть в десятковій системи числення число 1256.
3. Записати число у вигляді суми розрядних одиниць 23 524.
4. При якому значенні q правильні рівності: 10q = 1210; 312q + 213q = 14010.
5. Виконати дії і результат подати в десятковій системі числення:
4523256 + 213425 – 101112.
ІV. Підсумок




1. Поняття відношення подільності
Прямі операції (додавання і множення) над невід’ємними цілими числами виконуються завжди, а обернені (віднімання й ділення) – ні. Тому важливо знати при яких умовах виконуються обернені операції. Для виконання дії віднімання досить впевнитись в тому, що зменшуване не менше за від’ємник. Для ділення такої простої ознаки немає. Тому ще стародавні математики намагалися знайти правила, які допомагали б за записом числа а дізнатися, ділиться воно на число b чи ні, не виконуючи ділення а на b. В результаті пошуків були знайдені ознаки подільності цілих невід’ємних чисел.
Для встановлення таких ознак розглянемо поняття відношення подільності на множині цілих невід’ємних чисел.
Означення. Ціле невід’ємне число а ділиться на ціле невід’ємне число b, якщо існує таке ціле невід’ємне число q, що а = bq.
Відношення подільності числа а на число b символічно позначають а M b. Відношення подільності не означає операції, тому не можна писати а M b = q. Наприклад, число а = 24 ділиться на число b = 6, бо існує таке число q, що 24 = 6 × 4.
Означення. Нехай дано ціле невід’ємне число а і натуральне число b. Якщо при діленні з остачею а на b остача дорівнює нулю, то b називають дільником числа а, а число а називають кратним числу b.
Треба розрізняти відношення подільності і операцію ділення. Так, якщо а = 0 і b = 0, то а M b, бо рівність 0 = 0 × q виконується для будь-якого цілого невід’ємного числа q. Проте нуль не можна ділити на нуль, бо результат операції визначається неоднозначно.
Число а ≠ 0 не ділиться на нуль. Справді, якби існувало таке q, то а = 0 × q, що суперечить тому, що а ≠ 0.
Беручи до уваги рівність 0 = b × 0, дістанемо, що нуль ділиться на будь-яке ціле невід’ємне число. Якщо а M b і а < b, то а = 0. Якщо ж а ≠ 0 і а M b, то а ≥ b, тобто дільник даного числа а ≠ 0 не перевищує числа а. Тому множина всіх дільників такого числа - скінчена. Число 24 має такі дільники : 1, 2, 3, 4, 6, 8, 12, 24.
Чисел, кратних даному числу – нескінченна множина. Наприклад, усі парні числа кратні числу 2. Їх можна знайти за формулою x = 2q, де q набуває значення 0, 1, 2, 3, … .
Число 1 ділиться тільки само на себе. Числа 2, 3, 5, 7. . . діляться самі на себе і на одиницю. Числа 4, 6, 8, 9, … мають більше двох дільників. Ці спостереження привели математиків до понять простого і складеного числа.
Означення. Натуральне число, яке ділиться тільки на одиницю і на само себе, називається простим.
Отже, числа 2, 3, 5, 7 — прості натуральні.
Означення. Натуральне число, яке має більше двох дільників,  називається складеним.
називається складеним.
Такими числами є 4, 6, 8, 9. Так, число 6 має дільники 1, 2, 3, 6. Оскільки число 1 має тільки один дільник, то його не відносять ні до простих, ні до складених.
2. Властивості відношення подільності
Оскільки для будь-якого невід'ємного цілого числа а виконується рівність а = а × 1, тобто будь-яке ціле невід'ємне число ділиться само на себе (а 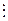 а), то відношення подільності на цій множині чисел — рефлексивне.
а), то відношення подільності на цій множині чисел — рефлексивне.
Для невід'ємних цілих чисел а і b, для яких виконуються відношення а 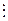 b і b
b і b 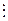 a й, маємо, що а = b, тобто відношення подільності невід'ємних цілих чисел антисиметричне.
a й, маємо, що а = b, тобто відношення подільності невід'ємних цілих чисел антисиметричне.
Справді, (a 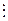 b) Þ
b) Þ 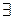 q (а =bq)
q (а =bq) 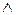 (b
(b 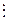 а) Þ
а) Þ 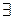 q1(b = а .q1), тому а = аqq1, звідки qq1 = 1. Це може бути тоді і тільки тоді, коли q=q1 =1.
q1(b = а .q1), тому а = аqq1, звідки qq1 = 1. Це може бути тоді і тільки тоді, коли q=q1 =1.
 |  |
Зрозуміло, що для різних чисел а і b з того, що а
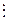 b, випливає, що b
b, випливає, що b 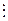 а. Це очевидно у випадку, коли а = 0, а b
а. Це очевидно у випадку, коли а = 0, а b 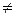 0. Якщо ж а і b — натуральні числа, то (а
0. Якщо ж а і b — натуральні числа, то (а 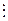 b) Þ (а
b) Þ (а 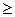 b). Оскільки а і b різні числа, то а > b. Отже, b
b). Оскільки а і b різні числа, то а > b. Отже, b 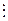 а.
а. Відношення подільності транзитивне, тобто з того, що (а 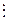 b)
b) 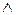 (b
(b 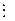 c) Þ (а
c) Þ (а 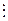 с). Справді, (а
с). Справді, (а 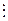 b) Þ
b) Þ 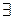 q (а =bq), (b
q (а =bq), (b 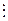 с)) Þ
с)) Þ 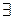 q1 (b = сq1). Тому a = bq = сqq1 = сq2. Отже, а
q1 (b = сq1). Тому a = bq = сqq1 = сq2. Отже, а 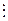 с.
с.
 |  |
Як бачимо, відношення подільності (
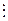 ) на множині Nо цілих невід'ємних чисел має властивості рефлексивності, антисиметричності і транзитивності, тобто є відношенням нестрогого порядку на множині Nо, причому часткового порядку, бо не кожна пара невід'ємних цілих чисел знаходиться у відношенні подільності. Наприклад, 4
) на множині Nо цілих невід'ємних чисел має властивості рефлексивності, антисиметричності і транзитивності, тобто є відношенням нестрогого порядку на множині Nо, причому часткового порядку, бо не кожна пара невід'ємних цілих чисел знаходиться у відношенні подільності. Наприклад, 4 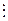 З і 3
З і 3 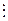 4.
4. Якщо число ділиться на 3, то воно має вигляд 3q. Якщо ж число не ділиться на 3, то воно при діленні на 3 матиме остачу. Оскільки остача повинна бути менша від 3, то вона дорівнюватиме 1 або 2.
3. Достатня умова подільності суми (різниці)
З теоретичної точки зору часто важливо знати, чи узгоджується відношення подільності на множині N0 з арифметичними операціями. На практиці часто виникає питання: як, не виконуючи операцій, визначити, ділиться чи ні на дане число певний числовий вираз. Наприклад, чи можна розділити порівну між трьома учнями 21 зошит . у клітинку і 18 у лінійку?
Є ознаки, які дають змогу, не обчислюючи результату, дізнатися, чи ділиться на певне число сума, різниця, добуток або частка кількох цілих невід'ємних чисел.
Теорема(достатня умова подільності суми). Якщо кожний доданок ділиться на натуральне число п, то й їхня сума теж ділиться на це число.
Доведення. Нехай а 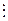 п і b
п і b 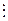 n. Тоді за означенням подільності а =nq2 і b = пq2, а тому а + b = пq1 + nq2= п (q2+q2). Отже, (а +b)
n. Тоді за означенням подільності а =nq2 і b = пq2, а тому а + b = пq1 + nq2= п (q2+q2). Отже, (а +b) 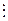 п. Теорему доведено.
п. Теорему доведено.
Аналогічно доводиться теорема для будь-якого числа доданків.
Чи є ця ознака подільності суми необхідною, тобто, чи буде істинним твердження: «Якщо сума ділиться на деяке число п, то й кожний доданок її ділиться на це число?» Ні, не буде. Наприклад 21 : 3, але ні 20, ні 1 не діляться на 3. Отже, достатня умова подільності суми не є необхідною. Обернене твердження виконується лише в окремих випадках, оскільки будь-яке натуральне число п> 2 можна зобразити у вигляді суми натуральних чисел кількома способами.
Теорема (достатняумова подільності різниці). Якщо а і b діляться на п і а ³ b, то а - b теж ділиться на п.
Доведення цієї теореми аналогічне попередньому.
Чи може ділитися сума двох доданків і один з них ділитися на дане число. якщо другий доданок не ділиться на це число? Ні, не може. Це дає змогу сформулювати необхідну й достатню умову подільності суми.
Теорема . Якщо один з двох доданків ділиться на дане число, то щоб їхня сума ділилася на це число, необхідно й достатньо, щоб і другий доданок ділився на це число.
Достатність умови випливає з першої теореми.
Необхідність. Нехай доданок а і сума а + b діляться на число п. Тоді (а+b) — а теж ділиться на число п. Отже, і число b також ділиться на число п.
Теорему доведено.
4. Достатня умова подільності добутку
Теорема(про подільність добутку). Якщо один з множників ділиться на натуральне число п, то й добуток ділиться на це число.
Доведення. Нехай множник а добутку аb ділиться на число п, тобто а = пq. Тоді аb = (пq) b = п (qb). Отже, аb 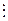 п.
п.
Теорему доведено.
Аналогічно доводиться твердження для більшого числа множників.
Наслідок. Якщо в добутку аb множник а ділиться на т, а множник b ділиться на п, то добуток аb ділиться на тп.
Наприклад, 24 · 36 ділиться на 108, бо 108 =12·9.
Доведені теореми використовуються при розв'язуванні відповідних задач.
Приклад. Довести, що добуток будь-яких двох послідовнихнатуральних чиселділиться на 2.
Розв'язання. Серед двох послідовних натуральних чисел одне обов'язково парне.Тому їхній добуток ділиться на 2.
