Предельные вероятности состояний

Рассмотрим марковский процесс с дискретными состояниями и непрерывным временем. Пример такого процесса: при работе электронного устройства возникают сбои. Если устройство дает сбой, то он немедленно обнаруживается, и обслуживающий персонал приступает к ремонту. Ремонт длится случайное время, затем электронное устройство снова в работе. Изобразим граф состояний:

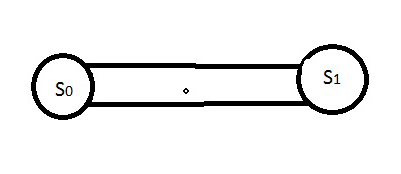S₀-электронное устройство функционирует,

S₁- ремонтируется

Переход системы из состояния S₀ в состояние S₁ будем представлять так: как только появится неисправность происходит мгновенный перескок системы из S₀ в S₁.Поток сбоев простейший с интенсивность 𝞴 сбоев в час.

После ремонта происходит мгновенный перескок системы из S₁ в S₀. Ремонт происходит с интенсивностью µ.

Назовём вероятностью j –го состояния вероятность P_j(t) того, что в момент t система будет находится в состоянии S_j. Очевидно, что для любого момента t сумма всех вероятностей состояний равна единице:

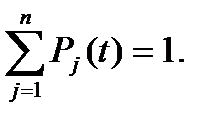
Имея в своём распоряжении граф, можно найти все вероятности состояний P_j(t) как функции времени. Для этого нужно составить уравнения Колмогорова.

Система S имеет два состояния. Рассмотрим состояние S₀.Определим вероятность P₀(t). Это вероятность того, что в момент t система будет в состоянии S₀. Придадим t малое приращение Δt и найдём P₀(t+Δt), т. е. в момент t+Δt система будет в состоянии S₀. Как это может произойти?

Очевидно, есть два варианта:

1) в момент t система была в состоянии S₀ и за время Δt не вышла из него;

2) в момент t система была в состоянии S₁, а за время Δt перешла в состояние S₀.

Первый вариант представляет произведение двух событий. Первое событие – в момент t система была в состоянии S₀, второе - за время Δt система не вышла из состояния S₀.Вероятность первого события P₀(t). Вероятность второго события вычислим через вероятность противоположного события: вероятность того, что за Δt система перейдёт в состояния S₁ равна 𝞴·Δt, вероятность того, что система за время Δt не выйдет из состояния S₀ равна 1-𝞴·Δt.

Тогда вероятность первого варианта равна произведению вероятностей этих событий, т. е. равна .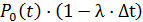

Второй вариант также представляет произведение двух событий: первое - в момент t система была в состоянии S₁, второе - за время Δt перешла в состояние S₀. Вероятность того, что - в момент t система была в состоянии S₁ равна 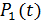; вероятность того, что система перейдёт из S₁вS₀равна 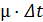. Вероятность второго варианта равна .

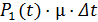Складывая вероятности обоих вариантов ( по правилу сложения вероятностей ), получим:

.

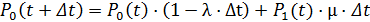Преобразуем это равенство и разделим обе части его на 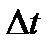, получим

.

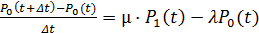Устремляя 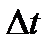к нулю, в пределе получим

.

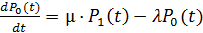Рассуждая аналогично для второго состояния S₁можно получить ещё дифференциальное уравнение

.

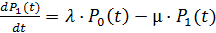Итак, получили систему двух уравнений.

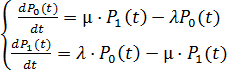(6)

К этой системе дифференциальных уравнений добавим ещё одно уравнение

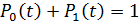. (7)

Одно уравнение лишнее. Можно одно из уравнений исключить ( допустим второе уравнение в системе (6) 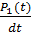). Тогда получим систему:

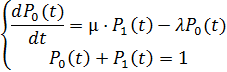
Уравнения Колмогорова – линейные дифференциальные уравнения с постоянными коэффициентами, которые можно решить аналитически, задав начальные условия, к примеру: .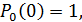

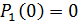Сформулируем правило составления уравнений Колмогорова:

в левой части каждого из них стоит производная j – го состояния;