Простые расширения числовых полей и их строение
ГДАВА I. ЭЛЕМЕНТЫ ТЕОРИИ ПОЛЕЙ
В этой главе будут рассматриваться числовые поля, т.е. подполя поля 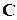 комплексных чисел, хотя аналогичная теория может быть построена для любого алгебраически замкнутого поля.
комплексных чисел, хотя аналогичная теория может быть построена для любого алгебраически замкнутого поля.
До сих пор изучались, в основном, числовые поля  рациональных чисел и
рациональных чисел и  действительных чисел. Однако многие задачи, в том числе задача о возможности построения с помощью циркуля и линейки того или иного числа, требуют рассмотрения и других числовых полей.
действительных чисел. Однако многие задачи, в том числе задача о возможности построения с помощью циркуля и линейки того или иного числа, требуют рассмотрения и других числовых полей.
Алгебраические числа и минимальные многочлены
Условимся, ради краткости, под полем понимать числовое поле, а под числом – комплексное число.
Определение 1. Пусть  – некоторое поле. Число
– некоторое поле. Число  называется алгебраическим относительно поля
называется алгебраическим относительно поля  (над полем
(над полем  ), если оно является корнем некоторого многочлена
), если оно является корнем некоторого многочлена  .
.
Если число  не является алгебраическим относительно поля
не является алгебраическим относительно поля  , то оно называется трансцендентным относительно
, то оно называется трансцендентным относительно  .
.
Замечание 1. Как известно, поле  является наименьшим числовым полем (т.е. содержится в любом числовом поле). В силу особого положения этого поля алгебраические и трансцендентные относительно поля
является наименьшим числовым полем (т.е. содержится в любом числовом поле). В силу особого положения этого поля алгебраические и трансцендентные относительно поля  числа называются просто алгебраическими и трансцендентными (без добавления слов «относительно поля
числа называются просто алгебраическими и трансцендентными (без добавления слов «относительно поля  »).
»).
Примеры.
1. Число  есть корень многочлена
есть корень многочлена  с рациональными коэффициентами и, следовательно, является алгебраическим.
с рациональными коэффициентами и, следовательно, является алгебраическим.
2. Любое число  из поля
из поля  является корнем многочлена
является корнем многочлена  и, следовательно, является алгебраическим относительно
и, следовательно, является алгебраическим относительно  .
.
3. Любое число  является алгебраическим относительно поля
является алгебраическим относительно поля  . Действительно, если
. Действительно, если  – вещественное число, то оно является корнем многочлена
– вещественное число, то оно является корнем многочлена  . Если
. Если  – мнимое число, то оно является корнем многочлена
– мнимое число, то оно является корнем многочлена  .
.
Долгое время считали, что все числа являются алгебраическими. Только в 1851 г. Эрмит обнаружил трансцендентное число  , а в 1882 г. Линдеман доказал трансцендентность числа
, а в 1882 г. Линдеман доказал трансцендентность числа  . Большой вклад в теорию трансцендентных чисел внес советский математик А.О. Гельфонд в 1931-36 гг. Из его результатов в частности следует, что трансцендентными являются числа вида
. Большой вклад в теорию трансцендентных чисел внес советский математик А.О. Гельфонд в 1931-36 гг. Из его результатов в частности следует, что трансцендентными являются числа вида  , где
, где  – целое,
– целое,  – иррационально (например,
– иррационально (например,  и т.д.), а также числа
и т.д.), а также числа  .
.
Замечание 2. Если существует биективное отображение  , то множества
, то множества  и
и  называется равномощными. Всякое множество, равномощное множеству
называется равномощными. Всякое множество, равномощное множеству  натуральных чисел называется счетным. Если же множество равномощно множеству
натуральных чисел называется счетным. Если же множество равномощно множеству  , то говорят, что оно имеет мощность континуума. Еще Кантор показал, что множество алгебраических чисел (как и множество
, то говорят, что оно имеет мощность континуума. Еще Кантор показал, что множество алгебраических чисел (как и множество  ) счетное, а множество трансцендентных чисел (как и множество иррациональных) имеет мощность континуума. Таким образом, трансцендентных чисел гораздо «больше», чем алгебраических.
) счетное, а множество трансцендентных чисел (как и множество иррациональных) имеет мощность континуума. Таким образом, трансцендентных чисел гораздо «больше», чем алгебраических.
Теорема 1. Если  – алгебраическое число над полем
– алгебраическое число над полем  , то
, то
1) существует единственный нормированный неприводимый в  многочлен
многочлен 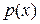 , корнем которого является число
, корнем которого является число  ;
;
2) если  – корень многочлена
– корень многочлена  , то
, то  .
.
□1) Согласно определению 1 в кольце  существует такой многочлен
существует такой многочлен  , что
, что  . Пусть
. Пусть

каноническое разложение многочлена  в произведение неприводимых над полем
в произведение неприводимых над полем  многочленов из
многочленов из  . Так как
. Так как  , то число
, то число  является корнем, по крайней мере, одного из нормированных неприводимых над полем
является корнем, по крайней мере, одного из нормированных неприводимых над полем  многочленов
многочленов  . Пусть
. Пусть  – любой другой многочлен с теми же свойствами. Так как
– любой другой многочлен с теми же свойствами. Так как  и
и  оба неприводимы, то они либо взаимно просты, либо ассоциированы (т.е. делятся друг на друга). Но если они взаимно просты в кольце
оба неприводимы, то они либо взаимно просты, либо ассоциированы (т.е. делятся друг на друга). Но если они взаимно просты в кольце  , то они взаимно просты и в кольце
, то они взаимно просты и в кольце  , а это противоречит тому, что они имеют общий корень
, а это противоречит тому, что они имеют общий корень  и, следовательно, в
и, следовательно, в  они делятся на
они делятся на  . Значит
. Значит  и
и  – ассоциированы. Но поскольку они нормированы, то они обязаны быть равными. Таким образом, многочлен
– ассоциированы. Но поскольку они нормированы, то они обязаны быть равными. Таким образом, многочлен  удовлетворяет требованиям 1) теоремы 1.
удовлетворяет требованиям 1) теоремы 1.
2) Пусть  – корень многочлена
– корень многочлена  из кольца
из кольца  и
и 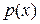 – найденный выше многочлен. Так как
– найденный выше многочлен. Так как 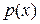 – неприводим, для любого многочлена
– неприводим, для любого многочлена  возможно лишь одно из двух: либо
возможно лишь одно из двух: либо  и
и 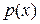 взаимно простые, либо
взаимно простые, либо  . Но первое невозможно, так как
. Но первое невозможно, так как  и
и 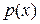 имеют общий корень
имеют общий корень  . Значит,
. Значит,  , что и требовалось доказать. ◘
, что и требовалось доказать. ◘
Определение 2. Нормированный неприводимый многочлен  , для которого алгебраическое относительно поля
, для которого алгебраическое относительно поля  число
число  является корнем, называется минимальным многочленом числа
является корнем, называется минимальным многочленом числа  , а степень минимального многочлена называется степенью алгебраического числа
, а степень минимального многочлена называется степенью алгебраического числа  .
.
Примеры.
4. Число  является алгебраическим числом 6 степени, а минимальным для него является многочлен
является алгебраическим числом 6 степени, а минимальным для него является многочлен  (он неприводим над полем
(он неприводим над полем  в силу признака Эйзенштейна).
в силу признака Эйзенштейна).
5. Всякое число  является корнем многочлена
является корнем многочлена  и, следовательно, является алгебраическим относительно поля
и, следовательно, является алгебраическим относительно поля  числом степени 1. Очевидно и наоборот – всякое алгебраическое относительно поля
числом степени 1. Очевидно и наоборот – всякое алгебраическое относительно поля  число степени 1 принадлежит полю
число степени 1 принадлежит полю  .
.
6. Относительно поля  все действительные числа имеют степень 1, а все мнимые – степень 2 (см. пример 3).
все действительные числа имеют степень 1, а все мнимые – степень 2 (см. пример 3).
Замечание 3. Если  – алгебраическое относительно поля
– алгебраическое относительно поля  число степени
число степени 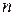 и поле
и поле 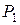 является расширением поля
является расширением поля  (т.е.
(т.е.  ), то
), то  является алгебраическим относительно поля
является алгебраическим относительно поля 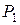 числом степени
числом степени  . Это следует из того, что неприводимый над полем
. Это следует из того, что неприводимый над полем  многочлен может оказаться приводим над его расширением. Например, число
многочлен может оказаться приводим над его расширением. Например, число  является алгебраическим числом степени 2 над полем
является алгебраическим числом степени 2 над полем  (минимальный многочлен
(минимальный многочлен  ) и алгебраическим относительно поля
) и алгебраическим относительно поля  числом степени 1 (минимальный многочлен
числом степени 1 (минимальный многочлен  ).
).
Теорема 2.Если 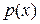 неприводим над каким-либо полем
неприводим над каким-либо полем  , то он не имеет в поле
, то он не имеет в поле 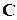 кратных корней.
кратных корней.
□ В силу закона контрапозиции достаточно доказать, что если  и имеет кратный корень в
и имеет кратный корень в 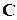 , то он приводим над полем
, то он приводим над полем  . Пусть
. Пусть  – кратный корень многочлена
– кратный корень многочлена 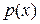 . Тогда
. Тогда  является также корнем его производной
является также корнем его производной  . Отсюда легко следует, что
. Отсюда легко следует, что  принадлежит кольцу
принадлежит кольцу  и имеет положительную степень. Значит,
и имеет положительную степень. Значит,  , где
, где  , т.е.
, т.е. 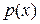 приводим над полем
приводим над полем  . ◘
. ◘
Простые расширения числовых полей и их строение.
Напомним, что если  является подполем поля
является подполем поля 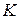 , то
, то 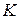 называется расширением поля
называется расширением поля  . В дальнейшем мы укажем некоторые типы расширений и изучим их структуру. Начнем с так называемых простых расширений.
. В дальнейшем мы укажем некоторые типы расширений и изучим их структуру. Начнем с так называемых простых расширений.
Пусть  – фиксированное поле и
– фиксированное поле и  – число. Рассмотрим множество всех полей, содержащих поле
– число. Рассмотрим множество всех полей, содержащих поле  и число
и число  . Это множество не пусто, так как само поле
. Это множество не пусто, так как само поле 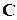 комплексных чисел принадлежит этому множеству. Пересечение всех этих полей также является полем, содержащим
комплексных чисел принадлежит этому множеству. Пересечение всех этих полей также является полем, содержащим  и
и  , причем это наименьшее по включению поле, содержащее
, причем это наименьшее по включению поле, содержащее  и
и  .
.
Определение 2. Пересечение всех полей, содержащих поле  и число
и число  , называется простым расширением поля
, называется простым расширением поля  с помощью числа
с помощью числа  и обозначается через
и обозначается через 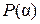 . Сам процесс расширения называется присоединением к полю
. Сам процесс расширения называется присоединением к полю  числа
числа  .
.
Если  – алгебраическое над полем
– алгебраическое над полем  число, то
число, то 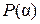 называют простым алгебраическим расширением, в противном случае – простым трансцендентным расширением поля
называют простым алгебраическим расширением, в противном случае – простым трансцендентным расширением поля  .
.
Теорема 1(о строении простого расширения).1)Простое расширение 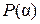 состоит из всевозможных чисел, представимых в виде частного значений многочленов из кольца
состоит из всевозможных чисел, представимых в виде частного значений многочленов из кольца  от числа
от числа  , т.е.
, т.е.
 (1)
(1)
2) Простое алгебраическое расширение состоит из чисел, представимых в виде значения многочленов из кольца  от числа
от числа  , т.е.
, т.е.
 . (2)
. (2)
□ 1) Обозначим через  правую часть равенства (1). Так как
правую часть равенства (1). Так как  и
и  , в силу свойств поля
, в силу свойств поля 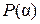 числа
числа
 ,
,  (3)
(3)
принадлежат 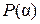 для любых неотрицательных чисел
для любых неотрицательных чисел 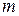 и
и  , т.е.
, т.е.  .
.
Обратно, так как  замкнуто относительно вычитания и деления, то
замкнуто относительно вычитания и деления, то  есть подполе поля
есть подполе поля 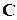 и, следовательно, поле. Кроме того, полагая в (3)
и, следовательно, поле. Кроме того, полагая в (3) 
 , получим, что
, получим, что  . Далее, считая в (3)
. Далее, считая в (3)  пробегающим все поле
пробегающим все поле  ,
,  , заключаем, что
, заключаем, что  . Но поскольку
. Но поскольку  – наименьшее поле, содержащее
– наименьшее поле, содержащее  и
и  , имеем включение
, имеем включение  . Учитывая теперь доказанное выше включение
. Учитывая теперь доказанное выше включение  , получаем равенство
, получаем равенство  . Таким образом, справедливость равенства (1) доказана.
. Таким образом, справедливость равенства (1) доказана.
2) Пусть теперь  – алгебраическое над полем
– алгебраическое над полем  число и
число и  обозначает правую часть равенства (2). Ясно, что
обозначает правую часть равенства (2). Ясно, что  . Так как
. Так как  замкнуто относительно вычитания и умножения, то оно является подкольцом поля
замкнуто относительно вычитания и умножения, то оно является подкольцом поля 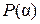 . Это кольцо коммутативное и имеет единицу. Докажем, что для каждого числа
. Это кольцо коммутативное и имеет единицу. Докажем, что для каждого числа  из
из  обратное к нему число
обратное к нему число  также принадлежит
также принадлежит  . Тем самым будет доказано, что
. Тем самым будет доказано, что  является полем.
является полем.
Пусть 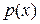 – минимальный многочлен алгебраического числа
– минимальный многочлен алгебраического числа  . Так как
. Так как  ,
,  , то
, то  не делится на
не делится на 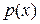 . Поскольку, кроме того,
. Поскольку, кроме того, 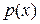 неприводим над полем
неприводим над полем  , многочлены
, многочлены 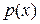 и
и  являются взаимно простыми. Но тогда в
являются взаимно простыми. Но тогда в  существуют такие многочлены
существуют такие многочлены  и
и  , что
, что
 . (4)
. (4)
Полагая здесь  , получим
, получим  или
или  .
.
Итак,  – поле, которое, очевидно, содержит
– поле, которое, очевидно, содержит  и
и  . В силу минимальности
. В силу минимальности 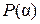 имеем
имеем  и, следовательно,
и, следовательно,  . ◘
. ◘
Замечание 1. Если  – трансцендентно над полем
– трансцендентно над полем  , то не все числа поля
, то не все числа поля 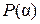 можно представить в виде
можно представить в виде  . Например, число
. Например, число  представимо в таком виде. Действительно, если предположить противное, т.е.
представимо в таком виде. Действительно, если предположить противное, т.е.  , то
, то  , т.е.
, т.е.  есть корень многочлена
есть корень многочлена  , что противоречит трансцендентности
, что противоречит трансцендентности  .
.
Примеры.
1. Найти  . Так как
. Так как  алгебраическое над полем
алгебраическое над полем  число, то по теореме 1
число, то по теореме 1  . Учитывая, что натуральные степени числа
. Учитывая, что натуральные степени числа  содержатся среди чисел
содержатся среди чисел  , заключаем, что
, заключаем, что  при любом
при любом 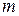 . Отсюда легко получаем, что
. Отсюда легко получаем, что  =С.
=С.
2. Найти  . Так как
. Так как  – трансцендентное число, то по теореме 1
– трансцендентное число, то по теореме 1  .
.
