Раздел 3. линейные образы Аналитической геометрии
Таблица 3.1. Используемые обозначения
| Обозначение | Наименование | ||||
| a, b a, b, c | отрезки, отсекаемые прямой на плоскости на осях координат отрезки, отсекаемые плоскостью на осях координат | ||||
| k k1, k2 | угловой коэффициент прямой на плоскости угловые коэффициенты прямых на плоскости | ||||
| M(x, y) M(x, y, z) | текущая точка прямой на плоскости текущая точка плоскости или прямой в пространстве | ||||
| Mo(xo, yo), M1(x1, y1), M2(x2, y2), M3(x3, y3) | координаты фиксированных точек на плоскости | ||||
| Mo(xo, yo, zo), M1(x1, y1, z1), M2(x2, y2, z2 ), M3(x3, y3, z3) | координаты фиксированных точек в пространстве | ||||
| n = (A, B) n1 = (A1, B1) n2 = (A2, B2) | нормальный вектор прямой на плоскости нормальные векторы прямых на плоскости | ||||
| n = (A, B, C) n1 = (A1, B1, C1) n2 = (A2, B2, C2) | нормальный вектор плоскости нормальные векторы плоскостей | ||||
| q = (l, m) q1 = (l1, m1) q2 = (l2, m2) | направляющий вектор прямой на плоскости направляющие векторы прямых на плоскости | ||||
| q =(l, m , n) q1 = (l1, m1, n1) q2 = (l2, m2, n2) | направляющий вектор прямой в пространстве 1) направляющие векторы прямых в пространстве 2) направляющие векторы плоскости | ||||
| r = (x, y) r = (x, y, z) | радиус-вектор текущей точки прямой на плоскости радиус-вектор текущей точки плоскости или прямой | ||||
| ro = (xo, yo) ro = (xo, yo, zo) | радиус-вектор фиксированной точки на плоскости радиус-вектор фиксированной точки в пространстве | ||||
| t | переменный параметр | ||||
| j | 1) угол между двумя прямыми на плоскости или в пространстве 2) угол между двумя плоскостями 3) угол между прямой и плоскостью | ||||
Таблица 3.2. Уравнения прямой на плоскости
| Уравнение | Наименование | Параметры |
| rn+ C = 0 | общее векторное уравнение прямой, проходящей перпендикулярно нормальному вектору | n = (A, B) – нормальный вектор прямой; (xo, yo), (x1, y1), (x2, y2) - координаты фиксированных точек на прямой; r = (x, y) – радиус-вектор текущей точки прямой; ro = (xo, yo) – радиус- вектор фиксированной точки на прямой; k - угловой коэффициент прямой; a - отрезок, отсекаемый прямой на оси 0x; b - отрезок, отсекаемый прямой на оси 0y; t - параметр; q = (l, m) - направляющий вектор прямой |
| r = ro + qt | векторное параметрическое уравнение прямой, проходящей через фиксированную точку параллельно направляющему вектору | |
| Ax + By + C = 0 | общее уравнение прямой | |
| A(x - xo)+B(y - yo) = 0 | уравнение прямой, проходящей через данную точку перпендикулярно данному направлению | |
| y = kx + b | уравнение прямой с данным угловым коэффициентом | |
| y - yo = k(x - xo) | уравнение прямой, проходящей через данную точку с данным угловым коэффициентом | |
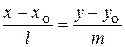 | каноническое уравнение прямой | |
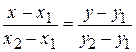 | уравнение прямой, проходящей через две точки | |
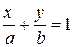 | уравнение прямой в отрезках | |
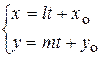 | параметрические уравнения прямой |
Таблица 3.3. Частные случаи положения прямой на плоскости
| № п/п | Случай | Уравнение | Нормальный вектор | График прямой L | |||
| A = 0, B ¹ 0, C ¹ 0, L || Ox | By + C = 0 или y = y1 | n = (0, B), n ^ Ox |  y L y L   y1 y1  n O x n O x | ||||
| B = 0, A ¹ 0, C ¹ 0, L || Oy | Ax + C = 0 или x = x1 | n = (A, 0), n ^ Oy |    Y L n Y L n
O x1 x | ||||
| C = 0, A ¹ 0, B ¹ 0, L проходит через начало координат | Ax + By = 0 или y = kx | n = (A, B) |   x L x L  n n
O x | ||||
| A = 0, C = 0, B ¹ 0, L совпадает с осью Ox | y = 0 | n = (0, 1), n ^ Ox |   x n L x n L   O x O x | ||||
| B = 0, C = 0, A ¹ 0, L совпадает с осью Oy | x = 0 | n = (1, 0), n ^ Oy |  x x   L n L n  O x O x |
Таблица 3.4. Взаимное расположение двух прямых на плоскости
| Прямые заданы уравнениями с параметрами | ||
| первой прямой: | второй прямой: | |
| n1 = (A1, B1), q1 = (l1, m1), k1 | n2 = (A2, B2), q2 = (l2, m2), k2 | |
| Угол между двумя прямыми | 1) cosj = 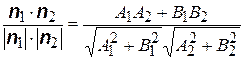 ; 2) cosj = ; 2) cosj = 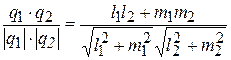 ; 3) tgj = ; 3) tgj = 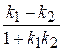 | |
| Условие параллельности | 1) n1||n2 Þ 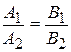 ; 2) q1||q2 Þ ; 2) q1||q2 Þ 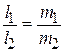 ; 3) k1 = k2 ; 3) k1 = k2 | |
| Условие перпендикулярности | 1) n1^n2 Þ n1×n2 = 0 или A1A2+B1B2 = 0 2) q1^q2 Þ q1×q2 = 0 или l1l2+m1m2 = 0 3) k1× k2 = -1 | |
Таблица 3.5. Уравнения плоскости в пространстве
| Уравнение | Наименование | Параметры | |
| rn+ D = 0 | общее векторное уравнение плоскости, проходящей перпендикулярно нормальному вектору | r = (x, y, z) – радиус-вектор текущей точки плоскости; n = (A, B, C) - нормальный вектор плоскости; q1и q2 – направляющие векторы плоскости; (xo, yo, zo), (x1, y1, z1), (x2, y2, z2 ), (x3, y3, z3) - координаты фиксированных точек на плоскости; a, b, c - отрезки, отсекаемые плоскостью на осях координат | |
| (q1´ q2)r+ D = 0 | векторное уравнение плоскости, проходящей, проходящей параллельно двум направляющим векторам | ||
| Ax+By+Cz+D = 0 | общее уравнение | ||
| A(x-xo)+B(y-yo) + + C(z-zo) = 0 | уравнение плоскости, проходящей через данную точку перпендикулярно данному направлению | ||
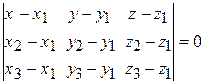 | уравнение плоскости, проходящей через три точки | ||
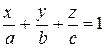 | уравнение плоскости в отрезках | ||
Таблица 3.6. Частные случаи положения плоскости в пространстве
| № п/п | Случай | Уравнение | Положение плоскости P |
| A = 0, B ¹ 0, C ¹ 0, D ¹ 0 | By + Cz + D = 0 | P || Ox | |
| B = 0, A ¹ 0, C ¹ 0, D ¹ 0 | Ax + Cz + D = 0 | P || Oy | |
| C = 0, A ¹ 0, B ¹ 0, D ¹ 0 | Ax + By + D = 0 | P || Oz | |
| D = 0, A ¹ 0, B ¹ 0, C ¹ 0 | Ax + By + Cz = 0 | P проходит через начало координат | |
| A = 0, B = 0, C ¹ 0, D ¹ 0 | Cz + D = 0 | P || Oxy | |
| A = 0, C = 0, B ¹ 0, D ¹ 0 | By + D = 0 | P || Oxz | |
| B = 0, C = 0, A ¹ 0, D ¹ 0 | Ax + D = 0 | P || Oyz | |
| A = 0, D = 0, B ¹ 0, C ¹ 0 | By + Cz = 0 | P проходит через ось Ox | |
| B = 0, D = 0, A ¹ 0, C ¹ 0 | Ax + Cz = 0 | P проходит через ось Oy | |
| C = 0, D = 0, A ¹ 0, C ¹ 0 | Ax + By = 0 | P проходит через ось Oz | |
| A = 0, B = 0, D = 0, C ¹ 0 | z = 0 | P совпадает с Oxy | |
| A = 0, C = 0, D = 0, B ¹ 0 | y = 0 | P совпадает с Oxz | |
| B = 0, C = 0, D = 0, A ¹ 0 | x = 0 | P совпадает с Oyz |
Таблица 3.7. Взаимное расположение двух плоскостей
| Плоскости заданы уравнениями с параметрами | ||
| первой плоскости: | второй плоскости: | |
| n1 = (A1, B1 , C1) | n2 = (A2, B2 , C2) | |
| Угол между двумя плоскостями | cosj = 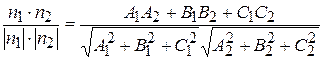 | |
| Условие параллельности | n1||n2 Þ 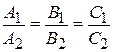 | |
| Условие перпендикулярности | n1 ^ n2 Þ n1×n2 = 0 или A1A2+B1B2 + C1C2= 0 | |
Таблица 3.8. Уравнения прямой в пространстве
| Уравнение | Наименование | Параметры |
| r = ro + qt | векторное параметрическое уравнение прямой, проходящей через фиксированную точку параллельно направляющему вектору | r = (x, y, z) – радиус-вектор текущей точки прямой; ro = (xo, yo, zo) – радиус-вектор фиксированной точки на прямой; n1 = (A1, B1, C1), n2 = (A2, B2, C2) - нормальные векторы плоскостей; |
| (r - ro) ´ q = o | векторное уравнение прямой, проходящей через фиксированную точку параллельно направляющему вектору | |
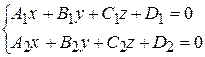 | общие уравнения прямой | |
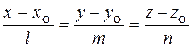 | канонические уравнения | q = (l, m, n) - |
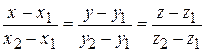 | уравнения прямой, проходящей через две фиксированные точки | направляющий вектор прямой; t - параметр; |
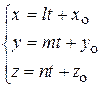 | параметрические уравнения прямой | (xo, yo, zo), (x1, y1, z1), (x2, y2, z2) - координаты фиксированных точек на прямой |
Таблица 3.9. Взаимное расположение двух прямых в пространстве
| Направляющие векторы | ||
| первой прямой: | второй прямой: | |
| q1 = (l1, m1, n1) | q2 = (l2, m2, n2) | |
| Угол между двумя прямыми | cosj = 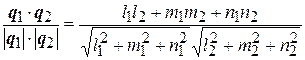 | |
| Условие параллельности | q1||q2 Þ 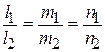 | |
| Условие ортогональности | q1 ^ q2 Þ q1×q2 = 0 или l1l2 + m1m2 + n1n2 = 0 | |
Таблица 3.10. Взаимное расположение прямой и плоскости
| Направляющий вектор прямой: | Нормальный вектор плоскости: |
| q = (l, m, n); точка на прямой: Mo(xo, yo, zo) | n = (A, B, C) |
| Угол между прямой и плоскостью | sinj = = 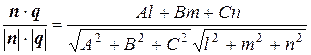 |
| Условие параллельности | n^q Þ n×q = 0 или Al + Bm + Cn = 0 |
| а) прямая не лежит в плоскости | Axo+ Byo+ Czo + D ¹ 0 |
| б) прямая лежит в плоскости | Axo+ Byo+ Czo + D = 0 |
| Условие пересечения прямой и плоскости | n×q ¹ 0 или Al + Bm + Cn ¹ 0 |
| Условие перпендикулярности | n||q Þ 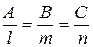 |
Таблица 3.11. Расстояние от точки до прямой на плоскости и до плоскости в
пространстве

