К степенным средним величинам относятся: средняя арифметическая простая и средняя арифметическая взвешенная, которые мы сейчас рассмотрим.
Рассмотрим первый показатель центральной тенденции – средняя (средняя величина).
Средняя величина показывает значение признака, распределённое поровну между всеми единицами совокупности.
1) По не сгруппированным данным. Средняя арифметическая простая, которая рассчитывается по формуле:
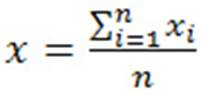
Подставив наши значения в формулу, находим:
Таблица 7
| Xср.млн.руб. | 205,129 |
| n |
Вывод: Таким образом, средняя квартальная выручка предприятия в период с 2005 по 2010 год составила 205,129 млн. рублей.
2) Средняя арифметическая взвешенная, которая рассчитывается по формуле:
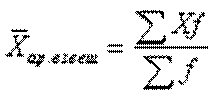
Чтобы рассчитать среднюю арифметическую взвешенную воспользуемся данными таблицы:
Таблица 8
| № | Интервал | Величина интервала | Кол-во кварталов | Сер.интер. |
| (166,6;167,8) | 1,2 | 167,2 | ||
| (167,8;170,1) | 2,3 | 168,95 | ||
| (170,1;173,6) | 3,5 | 171,85 | ||
| (173,6;178,3) | 4,7 | 175,95 | ||
| (178,3;184,2) | 5,9 | 181,25 | ||
| (184,2;191,2) | 187,7 | |||
| (191,2;199,4) | 8,2 | 195,3 | ||
| (199,4;208,8) | 9,4 | 204,1 | ||
| (208,8;219,3) | 10,5 | 214,05 | ||
| (219,3;231,0) | 11,7 | 225,15 | ||
| (231,0;243,9) | 12,9 | 237,45 | ||
| (243,9;258) | 14,1 | 250,95 |
Подставив наши значения в формулу, находим:
| Xвзв.млн.руб. | 203,935 |
Вывод: Таким образом, средняя квартальная выручка предприятия в период с 2005 по 2010 год составила 203, 935 млн. рублей.
1.4 Оценка структурных средних (моды, медианы) на основе структурной группировки
Мода – наиболее часто встречающееся в совокупности значение признака (наиболее типичное значение признаков).
Таблица 9
| № | Интервал | Величина интервала | Кол-во кварталов | Сер.интер. | Сумма накопленных частот |
| (166,6;167,8) | 1,2 | 167,2 | |||
| (167,8;170,1) | 2,3 | 168,95 | |||
| (170,1;173,6) | 3,5 | 171,85 | |||
| (173,6;178,3) | 4,7 | 175,95 | |||
| (178,3;184,2) | 5,9 | 181,25 | |||
| (184,2;191,2) | 187,7 | ||||
| (191,2;199,4) | 8,2 | 195,3 | |||
| (199,4;208,8) | 9,4 | 204,1 | |||
| (208,8;219,3) | 10,5 | 214,05 | |||
| (219,3;231,0) | 11,7 | 225,15 | |||
| (231,0;243,9) | 12,9 | 237,45 | |||
| (243,9;258) | 14,1 | 250,95 |
Мода рассчитывается по формуле:
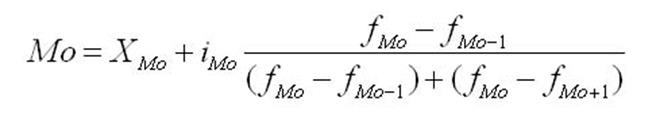
Найдём моду, для этого, во-первых, определим модальный интервал – группа с наибольшей частотой.
| Модальный интервал: | (208,8;219,3) |
Затем подставим данные в формулу и рассчитаем моду:
Таблица 10
| X0 | 208,8 |
| M0 | 215,8 |
Вывод: То есть наиболее часто встречающиеся значения квартальной выручки в период с 2005 по 2010 год около 215,8 млн. рублей.
Медиана – значение признака, делящего упорядоченную совокупность на две равные части, т.е. ровно половину совокупности имеет значение признака меньше медианы и ровно половину больше.
Медиана рассчитывается по формуле:
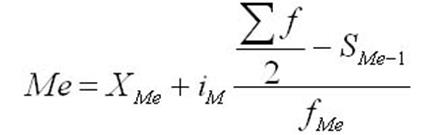
Найдём медиану, для этого, во-первых, рассчитаем накопленные частоты (суммарная частота всех групп от первой до текущей), которые представлены в таблице выше. Во-вторых, определим медианный интервал – интервал (группа), при котором сумма накопленных частот становится больше половины всей совокупности.
| Медианный интервал | (208,8;219,3) |
Затем найдём медиану по формуле, используя данные:
Таблица 11
| X0 | 208,8 |
| h | 10,5 |
| Me | 208,8 |
Вывод: То есть в период с 2005 по 2010 год в половине кварталов значения выручки не превышало 208,8 млн. рублей.
1.5 Оценка показателей вариации
Вариация – степень изменчивости признака в совокупности.
Для характеристики вариации используются абсолютные и относительные показатели.
Для начала рассмотрим и найдём абсолютные показатели.
Таблица 12
| № | Интервал | Кол-во кварталов | Величина интервала | Сер.интер. | lXiXвзв.l |
| (166,6;167,8) | 1,2 | 167,2 | 36,74 | ||
| (167,8;170,1) | 2,3 | 168,95 | 34,99 | ||
| (170,1;173,6) | 3,5 | 171,85 | 32,09 | ||
| (173,6;178,3) | 4,7 | 175,95 | 27,99 | ||
| (178,3;184,2) | 5,9 | 181,25 | 22,69 | ||
| (184,2;191,2) | 187,7 | 16,24 | |||
| (191,2;199,4) | 8,2 | 195,3 | 8,63 | ||
| (199,4;208,8) | 9,4 | 204,1 | 0,17 | ||
| (208,8;219,3) | 10,5 | 214,05 | 10,12 | ||
| (219,3;231,0) | 11,7 | 225,15 | 21,22 | ||
| (231,0;243,9) | 12,9 | 237,45 | 33,52 | ||
| (243,9;258) | 14,1 | 250,95 | 47,02 |
Продолжение таблицы
| lXi-Xвзв.l*fi | (Xi-Xвзв.)²*fi |
| 36,74 | 1349,460 |
| 69,97 | 2447,900 |
| 0,00 | |
| 111,94 | 50122,254 |
| 22,69 | 514,609 |
| 0,00 | |
| 8,63 | 74,563 |
| 0,50 | 0,735 |
| 50,58 | 12789,153 |
| 84,86 | 28804,878 |
| 67,03 | 8986,042 |
| 47,02 | 2210,410 |
| Xвзв. | 203,935 |
1) Первый абсолютный показатель - размах вариации, который рассчитывается по формуле:
R = Хmax- Xmin
Подставив наши значения в формулу, находим:
Таблица 13
| R(размах вариации) | 91,4 |
| Xmax | |
| Xmin | 166,6 |
Вывод: Таким образом, разница между максимальным и минимальным значением квартальной выручки в период с 2005 по 2010 год составила 91,4 млн. рублей.
2) Среднее линейное отклонение, которое рассчитывается по формуле:
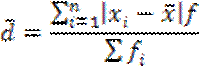
Подставив наши значения в формулу, находим
| đ | 41,66 |
3) Среднее квадратичное отклонение, которое рассчитывается по формуле:
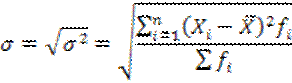
Подставив наши значения в формулу, находим
| σ | 94,560 |
Вывод: Среднее линейное и среднее квадратичное отклонение показывают, на сколько в среднем колеблются индивидуальные значения выручки от ее среднего значения, таким образом, индивидуальные значения выручки от её среднего значения в среднем колеблются на 41,66 млн. рублей и 92,56 млн. рублей.
4) Дисперсия, которая рассчитывается по формуле:
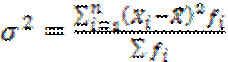
Подставив наши значения в формулу, находим
| σ² | 8941,667 |
Вывод: Дисперсия измеряет вариацию признака по всей совокупности в целом под влиянием всех факторов, обуславливающих эту вариацию.
Теперь рассмотрим относительные показатели.
1) Коэффициент осцилляции, который рассчитывается по формуле:
| R | 91,4 |
| Xвзв. | 203,935 |
| Xmax | |
| Xmin | 166,6 |
| R/Xвзв. | 0,45 |
| Vr(%) | 44,82% |
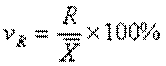Таблица 14
2) Линейный коэффициент вариации, который рассчитывается по формуле:
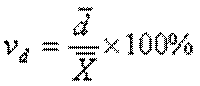
Таблица 15
| Xвзв. | 203,935 |
| đ | 41,66 |
| Vđ | 20,43% |
3) Коэффициент вариации, который рассчитывается по формуле:
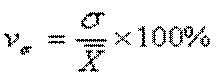
Таблица 16
| Xвзв. | 203,935 | σ | 94,560 |
| Vσ | 46,37% |
Вывод: Относительные показатели вариации характеризуют степень однородности совокупности, т.к. значения коэффициента вариации превышают 33%, то совокупность считается неоднородной.
1.6 Графическое представление распределения значений (гистограмма)
Для построения гистограммы необходимы данные о количествах кварталов и интервалы.
Таблица 17
| Интервал | Кол-во кварталов |
| (166,6;167,8) | |
| (167,8;170,1) | |
| (170,1;173,6) | |
| (173,6;178,3) | |
| (178,3;184,2) | |
| (184,2;191,2) | |
| (191,2;199,4) | |
| (199,4;208,8) | |
| (208,8;219,3) | |
| (219,3;231,0) | |
| (231,0;243,9) | |
| (243,9;258) |
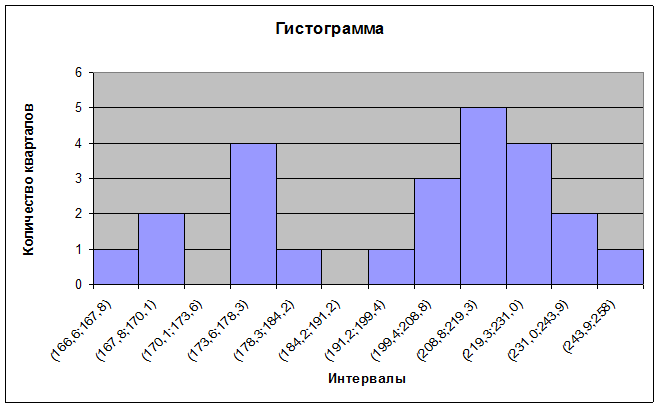
Рис.1
Вывод: Найденная по формуле и на рисунке 1 мода совпадает.
Для построения кумуляты необходимы данные о накопленных частотах и выручке.
Таблица 18
| 166,6 | |
| 167,8 | |
| 170,1 | |
| 173,6 | |
| 178,3 | |
| 184,2 | |
| 191,2 | |
| 199,4 | |
| 208,8 | |
| 219,3 | |
| 243,9 | |
| X | Сумма накопленных частот |
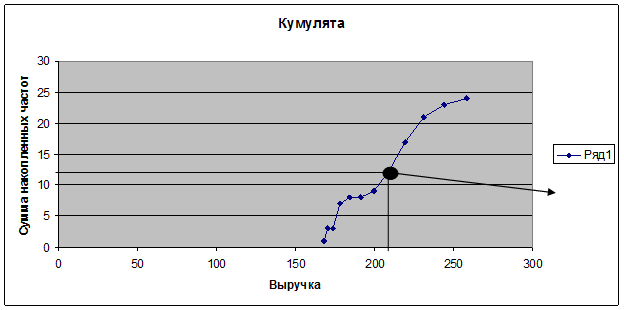
Рис. 2
2. Оценка абсолютных и относительных показателей динамики для выбранного показателя
Существуют абсолютные и относительные показатели при анализе рядов динамики.
В свою очередь ряд динамики – ряд изменяющихся во времени значений статистического показателя, расположенных в хронологическом порядке. Ряд динамики состоит из показателей уровней ряда и периодов времени(в нашем случае - кварталы).
Абсолютные статистические показатели - показатели, выражающие размеры конкретных общественных явлений. Абсолютные величины всегда числа именованные.
Все абсолютные статистические величины подразделяются на:
- индивидуальные - показатели, которые выражают размеры количественных признаков у отдельных единиц изучаемой совокупности (численность работников в фирме). Эти данные получаются в результате статистического и регистрируются в формулах наблюдения, и она используется для итоговых (общих) показателей.
- итоговые (общие, суммарные) выражают размеры, величину того или иного признака у всех единиц данной совокупности (численность рабочих шах даст общую численность работающих в стране). Такие данные используются для проведения группировки показателей, для сводки и для проведения анализа.
Абсолютные величины сами по себе не дают достаточной характеристики оценки явления. Поэтому в статистике наряду с абсолютными величинами используются относительные, которые представляют собой показатели, характеризующие количественные соотношения, присущие конкретным экономическим явлениям (удельный вес городского и сельского населения в общей численности). Отличительной особенностью относительных величин является то, что они обычно в отвлеченной форме выражают соотношение либо индивидуальных, либо суммарных абсолютных величин.
Абсолютные и относительные показатели, в свою очередь подразделяются на: цепные, базисные и средние.
Если сравнение производится с начальным (базисным) периодом или моментом времени в ряду динамики, то показатель называется базисным.
Если сравнение производится с предыдущим периодом или моментом времени в ряду динамики, то показатель называется цепным.
Средние показатели дают обобщённую характеристику ряда динамики, раскрывают основную его тенденцию.
Рассмотрим и найдём абсолютные показатели динамики:
1) Абсолютный прирост – показатель, характеризующий абсолютные изменения уровня ряда, произошедшие за определённый период времени.
1.1) Базисный абсолютный прирост
Находится по формуле:
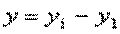
1.2) Цепной абсолютный прирост
Находится по формуле:
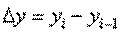
| Время | Выручка | ∆yi баз. | ∆yi цеп. |
| 1 кв.2005 | - | - | |
| 2 кв.2005 | 168,2 | -5,8 | -5,8 |
| 3 кв.2005 | 166,6 | -7,4 | -1,6 |
| 4кв.2005 | -4 | 3,4 | |
| 1кв.2006 | 178,3 | 4,3 | 8,3 |
| 2кв. 2006 | 180,7 | 6,7 | 2,4 |
| 3кв.2006 | 178,1 | 4,1 | -2,6 |
| 4кв.2006 | 174,1 | 0,1 | -4 |
| 1кв. 2007 | 30,9 | ||
| 2кв2007 | 208,2 | 34,2 | 3,2 |
| 3кв.2007 | 203,5 | 29,5 | -4,7 |
| 4кв.2007 | 197,5 | 23,5 | -6 |
| 1кв.2008 | 27,5 | ||
| 2кв.2008 | 221,3 | 47,3 | -3,7 |
| 3кв.2008 | 218,1 | 44,1 | -3,2 |
| 4кв2008 | 0,9 | ||
| 1кв.2009 | 226,5 | 52,5 | 7,5 |
| 2кв.2009 | 215,9 | 41,9 | -10,6 |
| 3кв.2009 | 218,4 | 44,4 | 2,5 |
| 4кв.2009 | 218,7 | 44,7 | 0,3 |
| 1кв.2010 | 11,3 | ||
| 2кв.2010 | 232,8 | 58,8 | 2,8 |
| 3кв.2010 | 235,2 | 61,2 | 2,4 |
| 4кв.2010 | 22,8 |
Таблица 19
Вывод: Таким образом, выручка в I квартале 2006 года увеличилась на 4,3 млн. руб. по сравнению с I кварталом 2005 года и увеличилась на 8,3 млн.руб. по сравнению с IV кварталом 2005 года.
Выручка в I квартале 2007 года увеличилась на 31 млн. руб. по сравнению с I кварталом 2006 года и увеличилась на 30,9 млн. руб. по сравнению с IV кварталом 2006 года.
Выручка в I квартале 2008 года увеличилась на 51 млн. руб. по сравнению с I кварталом 2007 года и увеличилась на 27,5 млн. руб. по сравнению с IV кварталом 2007 года.
Выручка в I квартале 2009 года увеличилась на 52,5 млн. руб. по сравнению с I кварталом 2008 года и увеличилась на 7,5 млн. руб. по сравнению с IV кварталом 2008 года.
Выручка в I квартале 2010 года увеличилась на 56 млн. руб. по сравнению с I кварталом 2009 года и увеличилась на 11,3 млн. руб. по сравнению с IV кварталом 2009 года.
2) Абсолютное ускорение
Находится по формуле:
∆'yi = ∆yi цеп. - ∆yi-1 цеп.
Таблица 20
| ∆yi баз. | ∆yi цеп. | ∆'yi |
| - | - | - |
| -5,8 | -5,8 | - |
| -7,4 | -1,6 | 4,2 |
| -4 | 3,4 | |
| 4,3 | 8,3 | 4,9 |
| 6,7 | 2,4 | -5,9 |
| 4,1 | -2,6 | -5 |
| 0,1 | -4 | -1,4 |
| 30,9 | 34,9 | |
| 34,2 | 3,2 | -27,7 |
| 29,5 | -4,7 | -7,9 |
| 23,5 | -6 | -1,3 |
| 27,5 | 33,5 | |
| 47,3 | -3,7 | -31,2 |
| 44,1 | -3,2 | 0,5 |
| 0,9 | 4,1 | |
| 52,5 | 7,5 | 6,6 |
| 41,9 | -10,6 | -18,1 |
| 44,4 | 2,5 | 13,1 |
| 44,7 | 0,3 | -2,2 |
| 11,3 | ||
| 58,8 | 2,8 | -8,5 |
| 61,2 | 2,4 | -0,4 |
| 22,8 | 20,4 |
Если значения абсолютного ускорения колеблются около «0», это говорит о равномерном росте показателя. Если абсолютное ускорение принимает отрицательные значения, это говорит о замедлении роста показателя.
3) Средний абсолютный прирост
Находится по формуле:
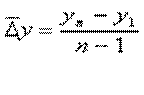
∆ср.y=(-5,8+(-1,6)+3,4+8,3+2,4+(-2,6)+(-4)+30,9+3,2+(-4,7)+(-6)+27,5+(-3,7)+
+(-3,2)+0,9+7,5+(-10,6)+2,5+0,3+11,3+2,8+2,4+22,8)/23=3,65
Вывод: За рассматриваемый период показатель увеличивался.
Рассмотрим и найдём относительные показатели динамики:
1) Темп роста – показывает во сколько раз текущий уровень ряда больше предыдущего, либо больше базисного (первоначального).
1.1) Базисный. Находится по формуле:
Тpi баз. = yi/y0 * 100%
1.2) Цепной. Находится по формуле:
Тpi цеп. = yi/yi-1 * 100%
Таблица 21
| Время | Выручка | Тpi баз. | Тpi цеп. |
| 1 кв.2005 | - | - | |
| 2 кв.2005 | 168,2 | 97% | 97% |
| 3 кв.2005 | 166,6 | 96% | 99% |
| 4кв.2005 | 98% | 102% | |
| 1кв.2006 | 178,3 | 102% | 105% |
| 2кв. 2006 | 180,7 | 104% | 101% |
| 3кв.2006 | 178,1 | 102% | 99% |
| 4кв.2006 | 174,1 | 100% | 98% |
| 1кв. 2007 | 118% | 118% | |
| 2кв2007 | 208,2 | 120% | 102% |
| 3кв.2007 | 203,5 | 117% | 98% |
| 4кв.2007 | 197,5 | 114% | 97% |
| 1кв.2008 | 129% | 114% | |
| 2кв.2008 | 221,3 | 127% | 98% |
| 3кв.2008 | 218,1 | 125% | 99% |
| 4кв2008 | 126% | 100% | |
| 1кв.2009 | 226,5 | 130% | 103% |
| 2кв.2009 | 215,9 | 124% | 95% |
| 3кв.2009 | 218,4 | 126% | 101% |
| 4кв.2009 | 218,7 | 126% | 100% |
| 1кв.2010 | 132% | 105% | |
| 2кв.2010 | 232,8 | 134% | 101% |
| 3кв.2010 | 235,2 | 135% | 101% |
| 4кв.2010 | 148% | 110% |
2) Темп прироста
2.1) Базисный. Находится по формуле:
Тпр.yi баз. = Тpyi баз. – 100%
2.2) Цепной. Находится по формуле:
Тпр.yi цеп. = Тpyi цеп. – 100%
Таблица 22
| Время | Выручка | Тpi баз. | Тpi цеп. | Тпр.yi баз.(%) | Тпр.yi цеп.(%) |
| 1 кв.2005 | - | - | - | - | |
| 2 кв.2005 | 168,2 | 97% | 97% | -3 | -3 |
| 3 кв.2005 | 166,6 | 96% | 99% | -4 | -1 |
| 4кв.2005 | 98% | 102% | -2 | ||
| 1кв.2006 | 178,3 | 102% | 105% | ||
| 2кв. 2006 | 180,7 | 104% | 101% | ||
| 3кв.2006 | 178,1 | 102% | 99% | -1 | |
| 4кв.2006 | 174,1 | 100% | 98% | -2 | |
| 1кв. 2007 | 118% | 118% | |||
| 2кв2007 | 208,2 | 120% | 102% | ||
| 3кв.2007 | 203,5 | 117% | 98% | -2 | |
| 4кв.2007 | 197,5 | 114% | 97% | -3 | |
| 1кв.2008 | 129% | 114% | |||
| 2кв.2008 | 221,3 | 127% | 98% | -2 | |
| 3кв.2008 | 218,1 | 125% | 99% | -1 | |
| 4кв2008 | 126% | 100% | |||
| 1кв.2009 | 226,5 | 130% | 103% | ||
| 2кв.2009 | 215,9 | 124% | 95% | -5 | |
| 3кв.2009 | 218,4 | 126% | 101% | ||
| 4кв.2009 | 218,7 | 126% | 100% | ||
| 1кв.2010 | 132% | 105% | |||
| 2кв.2010 | 232,8 | 134% | 101% | ||
| 3кв.2010 | 235,2 | 135% | 101% | ||
| 4кв.2010 | 148% | 110% |
Вывод: Таким образом, выручка за I квартал 2006 года увеличилась на 2 % по сравнению с I кварталом 2005 года и также увеличилась на 5 % по сравнению с IV кварталом 2005 года.
Таким образом, выручка за I квартал 2007 года увеличилась на 18 % по сравнению с I кварталом 2006 года и также увеличилась на 18 % по сравнению с IV кварталом 2006 года.
Таким образом, выручка за I квартал 2008 года увеличилась на 29 % по сравнению с I кварталом 2007 года и также увеличилась на 14 % по сравнению с IV кварталом 2007 года.
Таким образом, выручка за I квартал 2009 года увеличилась на 30 % по сравнению с I кварталом 2008 года и также увеличилась на 3 % по сравнению с IV кварталом 2008 года.
Таким образом, выручка за I квартал 2010 года увеличилась на 32 % по сравнению с I кварталом 2009 года и также увеличилась на 5 % по сравнению с IV кварталом 2009 года.
3) Средний темп роста. Находится по формуле:
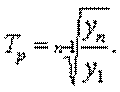
Тр = 258/174^1/23=1,02 (102 %)
3. Выравнивание ряда методом скользящей средней
Суть метода состоит в исключении случайных колебаний путем расчета средних значений по «скользящим» укрупненным интервалам (интервалу сглаживания).
Для этого нам понадобятся данные о выручке и кварталах.
3-х уровневая скользящая средняя находится по формуле:
yср.t = (yt-1 + yt + yt+1)/3
Найдём значения для каждого квартала:
yср.2 = (174+168,2+166,6)/3= 169,6
yср.3 = (168,2+166,6+170)/3= 168,3
yср.4 = (166,6+170+178,3)/3= 171,6
yср.5 = (170+178,3+180,7)/3= 176,3
yср.6 = (178,3+180,7+178,1)/3= 179,0
yср.7 = (180,7+178,1+174,1)/3= 177,6
yср.8 = (178,1+174,1+205)/3= 185,7
yср.9 = (174,1+205+208,2)/3= 195,8
yср.10 = (205+208,2+203,5)/3= 205,6
yср.11 = (208,2+203,5+197,5)/3= 203,1
yср.12 = (203,5+197,5+225)/3= 208,7
yср.13 = (225+197,5+221,3)/3= 214,6
yср.14 = (225+221,3+218,1)/3= 221,5
yср.15 = (221,3+218,1+219)/3= 219,5
yср.16 = (218,1+219+226,5)/3= 221,2
yср.17 = (219+226,5+215,9)/3= 220,5
yср.18 = (226,5+215,9+218,4)/3= 220,3
yср.19 = (215,9+218,4+218,7)/3= 217,7
yср.20 = (218,4+218,7+230)/3= 222,4
yср.21 = (218,7+230+232,8)/3= 227
yср.22 = (230+232,8+235,2)/3= 232,7
yср.23 = (232,8+235,2+258)/3= 242
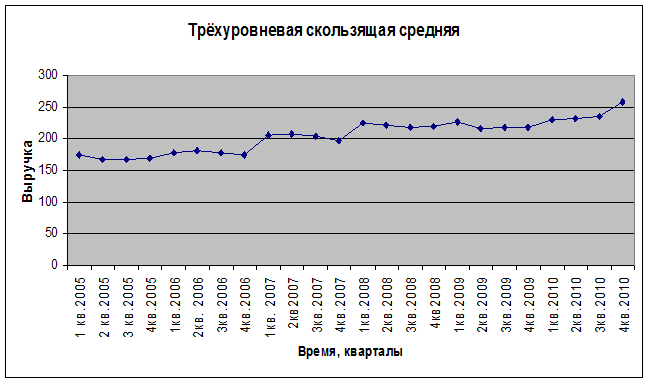
Рис.3
Вывод: По исходному графику четкую тенденцию к росту определить сложно. После проведения трехуровневого сглаживания тенденция к росту прослеживается лучше и можно предположить, что тенденция идёт к возрастанию.
По формуле: yср.t=(yt+2 + yt+1 + yt…+yt-1+yt-2)/5 рассчитываем точно также пяти уровневую скользящую среднюю.
Таблица 23
| Время | Выручка | y 3 ур. | y 5 ур. |
| 1 кв.2005 | - | - | |
| 2 кв.2005 | 168,2 | 169,6 | - |
| 3 кв.2005 | 166,6 | 168,3 | 171,42 |
| 4кв.2005 | 171,6 | 172,76 | |
| 1кв.2006 | 178,3 | 176,3 | 174,74 |
| 2кв. 2006 | 180,7 | 176,24 | |
| 3кв.2006 | 178,1 | 177,6 | 183,24 |
| 4кв.2006 | 174,1 | 185,7 | 189,22 |
| 1кв. 2007 | 195,8 | 193,78 | |
| 2кв2007 | 208,2 | 205,6 | 197,66 |
| 3кв.2007 | 203,5 | 203,1 | 207,84 |
| 4кв.2007 | 197,5 | 208,7 | 211,1 |
| 1кв.2008 | 214,6 | 213,08 | |
| 2кв.2008 | 221,3 | 221,5 | 216,18 |
| 3кв.2008 | 218,1 | 219,5 | 221,98 |
| 4кв2008 | 221,2 | 220,16 | |
| 1кв.2009 | 226,5 | 220,5 | 219,58 |
| 2кв.2009 | 215,9 | 220,3 | 219,7 |
| 3кв.2009 | 218,4 | 217,7 | 221,9 |
| 4кв.2009 | 218,7 | 222,4 | 223,16 |
| 1кв.2010 | 227,02 | ||
| 2кв.2010 | 232,8 | 232,7 | 234,94 |
| 3кв.2010 | 235,2 | - | |
| 4кв.2010 | - | - |
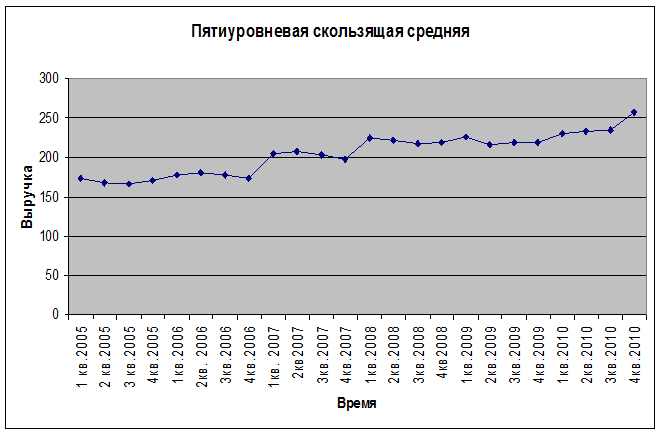
Рис.4
Вывод: После проведения 5-уровневого сглаживания тенденция к возрастанию видна достаточно отчетливо.
Затем находим семи уровневую скользящую среднюю, по формуле:
yср.t=(yt+3 + yt+2 + yt+1 + yt…+yt-1 + yt-2 +yt-3)/7
Таблица 24
| Время | Выручка | y 7ур. |
| 1 кв.2005 | - | |
| 2 кв.2005 | 168,2 | - |
| 3 кв.2005 | 166,6 | - |
| 4кв.2005 | 173,7 | |
| 1кв.2006 | 178,3 | 173,7 |
| 2кв. 2006 | 180,7 | 179,0 |
| 3кв.2006 | 178,1 | 184,9 |
| 4кв.2006 | 174,1 | 189,7 |
| 1кв. 2007 | 192,4 | |
| 2кв2007 | 208,2 | 198,8 |
| 3кв.2007 | 203,5 | 204,9 |
| 4кв.2007 | 197,5 | 211,2 |
| 1кв.2008 | 213,2 | |
| 2кв.2008 | 221,3 | 215,8 |
| 3кв.2008 | 218,1 | 217,6 |
| 4кв2008 | 220,6 | |
| 1кв.2009 | 226,5 | 219,7 |
| 2кв.2009 | 215,9 | 220,9 |
| 3кв.2009 | 218,4 | 223,0 |
| 4кв.2009 | 218,7 | 225,4 |
| 1кв.2010 | 229,9 | |
| 2кв.2010 | 232,8 | - |
| 3кв.2010 | 235,2 | - |
| 4кв.2010 | - |
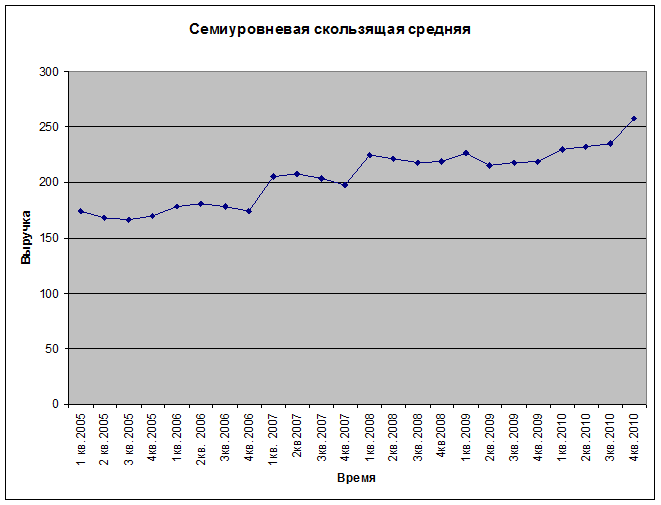
Рис.5
Вывод: После проведения 7-уровневого сглаживания, на графике четко прослеживается тенденция к росту.
4. Выявление наличия тренда в рассматриваемых рядах (проверка гипотезы о разности средних у первой и второй половины ряда)
Для выявления наличия тренда в динамическом ряду основной тенденции (тренда) рекомендуется использовать метод средних. Он основан на проверке гипотезы о статистической значимости отличия от нуля разности средних для первой и второй половины.
1) Разбиваем ряд на 2 половины.
| 1 кв.2005 | 1кв.2008 | ||
| 2 кв.2005 | 168,2 | 2кв.2008 | 221,3 |
| 3 кв.2005 | 166,6 | 3кв.2008 | 218,1 |
| 4кв.2005 | 4кв2008 | ||
| 1кв.2006 | 178,3 | 1кв.2009 | 226,5 |
| 2кв. 2006 | 180,7 | 2кв.2009 | 215,9 |
| 3кв.2006 | 178,1 | 3кв.2009 | 218,4 |
| 4кв.2006 | 174,1 | 4кв.2009 | 218,7 |
| 1кв. 2007 | 1кв.2010 | ||
| 2кв2007 | 208,2 | 2кв.2010 | 232,8 |
| 3кв.2007 | 203,5 | 3кв.2010 | 235,2 |
| 4кв.2007 | 197,5 | 4кв.2010 |
2) Рассчитываем для каждой группы среднюю величину:
yср.1 = (174 + 168,2 + 166,6 + 170 + 178,3 + 180,7 + 178,1 + 174,1 +205+
+ 208,2 + 203,5 +197,5)/12 = 2204,2/12 = 183,7
yср.2 =(225 + 221,3 + 218,1 + 219 + 226,5 + 215,9 + 218,4 + 218,7 + 230 +
+ 232,8 + 235,2 + 258)/12 = 2718,9/12 = 226,6
3)На основе расчетов можно выдвинуть гипотезу о различии средних. Проверка гипотезы осуществляется на основе t-критерия Стьюдента, который рассчитывается по формуле:
t = (y1ср.-y2ср.)/( σ*((1/n1+1/n2))^1/2 )
σ = ( ( (n1-1)* σ1²+(n2-1)* σ2² ) / n1+n2-2 ) ^1/2, где
y1ср – среднее значение для ряда первой половины;
y2ср – среднее значение для ряда второй половины;
σ1² и σ2² - дисперсии уровней ряда для 1 и 2 половины;
n1 и n2 – число уровней ряда в 1 и 2 половине соответственно.
4) Рассчитаем дисперсию:
σ1 = 217,7 (рассчитали с помощью Excell и функции «ДИСПР»)
σ2 = 126,2
n1 = 12, n2=12 соответственно
σ1² = 47393,3
σ2² = 15926,4
5) Рассчитаем среднее квадратическое отклонение:
σ =( ( (12-1)*47393,3+(12-1)*15926,4 )/12+12-2 )^1/2 = ((521326,3+175190,4)/22)^1/2 = 177,9
tкритерий = (183,7-226,6)/(177,9*(1/12+1/12)^1/2) = -42,9/(177,9*0,4) =
= -42,9/71,16 = -0,6
tтабличное= 2,9 (с помощью функции «СТЬЮДРАСПОБР»)
Сравнив табличное и расчётное –t – табличное значение больше, чем t – расчётное по модулю. Отсюда 2,9>-0,6, гипотеза о наличии тренда на 10% уровне значимости отклоняется. Подбором мы установили, что гипотеза о наличии тренда не может быть принята на любом уровне значимости. (Т.к. на 99% уровне tтабличное=1,8).
Проверим гипотезу о разности средних у первой половины ряда:
Xi – середина интервала;
Xср. = 203,935 (считали в пункте 1.3).
Таблица 25
| Сер.интер. | (Xi-Xср.) | (Xi-Xср.)² |
| - | - | - |
| 171,1 | -32,8 | 1078,1 |
| 167,4 | -36,5 | 1334,8 |
| 168,3 | -35,6 | 1269,9 |
| 174,2 | -29,8 | 887,1 |
| 179,5 | -24,4 | 597,1 |
| 179,4 | -24,5 | 602,0 |
| 176,1 | -27,8 | 774,8 |
| 189,6 | -14,4 | 206,9 |
| 206,6 | 2,7 | 7,1 |
| 205,9 | 1,9 | 3,7 |
| 200,5 | -3,4 | 11,8 |
Проверим гипотезу о разности средних у второй половины ряда:
Таблица 26
| Сер.интер. | (Xi-Xср.) | (Xi-Xср.)² |
| 211,3 | 7,3 | 53,5 |
| 223,2 | 19,2 | 369,2 |
| 219,7 | 15,8 | 248,5 |
| 218,6 | 14,6 | 213,6 |
| 222,8 | 18,8 | 354,0 |
| 221,2 | 17,3 | 298,1 |
| 217,2 | 13,2 | 174,6 |
| 218,6 | 14,6 | 213,6 |
| 224,4 | 20,4 | 416,8 |
| 231,4 | 27,5 | 754,3 |
| 234,0 | 30,1 | 903,9 |
| 246,6 | 42,7 | 1820,3 |
Рассчитанное значение t меньше табличного (2,9>-0,6 ),значит можно сделать вывод об отсутствии тренда.
5. Аналитическое выравнивание (построение тренда), прогноз при помощи тренда на 3 периода вперед
Под аналитическим выравниванием понимают определение основной проявляющейся во времени тенденции развития изучаемого явления. Развитие предстает перед исследователем как бы в зависимости только от течения времени. В итоге выравнивания временного ряда получают наиболее общий, суммарный, проявляющийся во времени результат действия всех причинных факторов. Отклонение конкретных уровней ряда от уровней, соответствующих общей тенденции, объясняют действием факторов, проявляющихся случайно или циклически. В результате приходят к трендовой модели.
ŷ = a0 + a1t
Таблица 27
| t | t² | y*t |
| -12 | -2088 | |
| -11 | -1850,2 | |
| -10 | -1666 | |
| -9 | -1530 | |
| -8 | -1426,4 | |
| -7 | -1264,9 | |
| -6 | -1068,6 | |
| -5 | -870,5 | |
| -4 | -820 | |
| -3 | -624,6 | |
| -2 | -407 | |
| -1 | -197,5 | |
| 442,6 | ||
| 654,3 | ||
| 1132,5 | ||
| 1295,4 | ||
| 1528,8 | ||
| 1749,6 | ||
| 2587,2 | ||
| ∑t=0 | ∑t²=1300 | ∑yt=4171,7 |
1) Найдём коэффициент уравнения при помощи метода наименьших квадратов
A0*n + a1* ∑t = ∑y,
A0*∑t = a1*∑t² = ∑yt
2) Сложим и найдём сумму всех значений выручки:
∑y = 174 + 168,2 + 166,6 + 170 + 178,3 + 180,7 + 178,1 + 174,1 +205+ 208,2 +
+ 203,5 +197,5 + 225 + 221,3 + 218,1 + 219 + 226,5 + 215,9 + 218,4 +218,7 + +230 + 232,8 + 235,2 + 258 = 4923,1
3) Выразим a0:
a0 = ∑y/n
Выразим a1:
a1 = ∑yt/∑t²
Найдём эти значения:
a0 = 4923,1 /24 = 205,13
a1 = 4171,7 /1300 = 3,21
4) Отсюда составляем уравнение тренда:
ŷ = 205,13 + 3,21t
5) Подставим t в уравнение:
ŷI05 = 205,13 + 3,21*(-12) = 205,13 – 38,52 = 166,61 (на I квартал 2005 года)
ŷII05 = 205,13 + 3,21*(-11) = 169,82
ŷIII05 = 205,13 + 3,21*(-10) = 173,03
ŷIV05 = 205,13 + 3,21*(-9) = 176,24
ŷI06 = 205,13 + 3,21*(-8) = 179,45
ŷII06 = 205,13 + 3,21*(-7) = 182,66
ŷIII06 = 205,13 + 3,21*(-6) = 185,87
ŷIV06 = 205,13 + 3,21*(-5) = 189,08
ŷI07 = 205,13 + 3,21*(-4) = 192,29
ŷII07 = 205,13 + 3,21*(-3) = 195,5
ŷIII07 = 205,13 + 3,21*(-2) = 198,71
ŷIV07 = 205,13 + 3,21*(-1) = 201,92
ŷI08 = 205,13 + 3,21*1 = 208,34
ŷII08 = 205,13 + 3,21*2 = 211,55
ŷIII08 = 205,13 + 3,21*3 = 214,76
ŷIV08 = 205,13 + 3,21*4 = 217,97
ŷI09 = 205,13 + 3,21*5 = 221,18
ŷII09 = 205,13 + 3,21*6 = 224,39
ŷIII09 = 205,13 + 3,21*7 = 227,6
ŷIV09 = 205,13 + 3,21*8 = 230,81
ŷI10 = 205,13 + 3,21*9 = 234,02
ŷII10 = 205,13 + 3,21*10 = 237,23
ŷIII10 = 205,13 + 3,21*11 = 240,44
ŷIV10 = 205,13 + 3,21*12 = 243,65
6) Составим прогноз на 3 квартала вперёд:
ŷt = 205,13 + 3,21*13 = 205,13 + 41,73 = 246,86 (прогноз на I квартал 2011)
ŷt = 205,13 + 3,21* 14 = 205,13 +44,94 = 250,07 (прогноз на II квартал 2011)
ŷt = 205,13 + 3,21*15 = 205,13 +48,15 = 253,28 (прогноз на III квартал 2011)
Вывод: На I квартал 2011 года по прогнозным данным квартальная вырчука будет составлять 246,86 млн. руб., на II квартал - 250,07 млн.руб. и на III квартал 2011 года - 253,28 млн.руб. Из этих данных видно, что тренд имеет тенденцию к возрастанию.
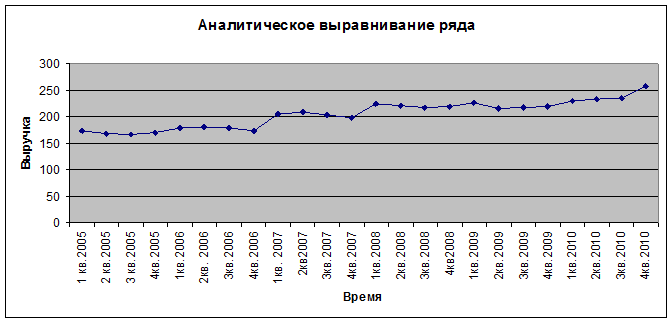
Рис. 6
Вывод: Тенденция идёт к возрастанию.
6. Анализ колеблемости динамического ряда, расчет индексов сезонности (если возможно)
Колебаниями уровней динамических рядов называют их отклонения от тренда, выражающего тенденцию изменения уровней. Колебания – процесс, протекающий во времени.В анализе колеблемости выделяют:
1) установление самого факта колебаний в динамическом ряду и периода колебаний;
2) учёт колебаний при моделировании ряда и прогнозировании.
Если тренда нет или он незначителен, то для каждого месяца (квартала) индекс рассчитывается по формуле:
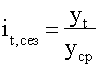
где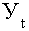 
-- уровень показателя за месяц (квартал) t;
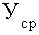-- общий уровень показателя.
Таким образом, средняя выручка:
в I квартале на 0,65% больше, чем средний объем чистой прибыли за весь рассматриваемый период;
во II квартале меньше на -0,30% , чем средний объем чистой прибыли за весь рассматриваемый период;
в III квартале меньше на -0,88%, чем средний объем чистой прибыли за весь рассматриваемый период;
в IV квартале больше на 0,53%%, чем средний объем чистой прибыли за весь рассматриваемый период.
Таблица 28
| квартал | ||||||
| I | 178,3 | 226,5 | ||||
| II | 168,2 | 180,7 | 208,2 | 221,3 | 215,9 | 232,8 |
| III | 166,6 | 178,1 | 203,5 | 218,1 | 218,4 | 235,2 |
| IV | 174,1 | 197,5 | 218,7 | |||
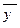 | 169,7 | 177,8 | 203,55 | 220,85 | 219,88 |
 |  |  |
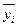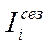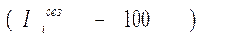| 206,47 | 100,65% | 0,65% |
| 204,52 | 99,70% | -0,30% |
| 203,32 | 99,12% | -0,88% |
| 206,22 | 100,53% | 0,53% |
| 205,13 |
Проведем анализ колеблемости ряда. Для оценки колеблемости уровня ряда используют показатель среднеквадратическое отклонение индексов сезонности (в долях ед.):
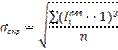
Проведем дополнительные расчеты:
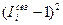
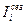Таблица 29
| Квартал | , в долях | |
| 1 кв. | 0,01 | 0,98 |
| 2 кв. | -0,003 | 1,01 |
| 3 кв. | -0,01 | 1,02 |
| 4 кв. | 0,01 | 0,98 |
| ∑ | 3,99 |
σсез. = (3,99/4)^1/2= 1млн. руб.
Чем меньше среднее квадратичное отклонение индексов сезонности, тем меньше величина сезонных колебаний.
7. Экспоненциальное сглаживание динамического ряда (метод выбирается в зависимости от наличия в динамическом ряду тренда и цикла)
Для анализа основной тенденции воспользуемся методом простого экспоненциального сглаживания:
yср.t= Аyt + (1-А)yср.t-1 = yср.t-1 + А*[yt-yср.t-1], где
А - сглаживающая константа (0<A<1),
yt- фактическое значение признака в t-1 период,
yср.t - сглаженное значение признака в t-1 период.
Берем А=0,8 (позволяет получить сглаженный ряд близкий к исходному) и проведем сглаживание:
Проведём трёхуровневую скользящую среднюю для показателя чистая прибыль:
уср.2 =(45,1+42,7+41,4) /3 = 43,07
уср.3 = (42,7+41,4+36,6)/3 =40,23
уср.4 = (36,6+41,4+43,7)/3 =40,57
уср.5 =(41,4+43,7+44,9) /3 =43,33
уср. 6=(43,7+44,9+42,4) /3 =43,67
уср.7 =(44,9+42,4+35,6) /3 =40,97
уср.8 =(42,4+35,6 + 50,1) /3 =42,7
уср9 = (35,6 + 50,1+54,8)/3 =46,83
уср.10 =(50,1+54,8+49,4) /3 =51,43
уср.11 =(54,8+49,4+43,8) /3 =49,33
уср.12 = (49,4+43,8+38,8)/3 =44
уср.13 =(43,8+38,8+35,7) /3 =39,43
уср.14 = (38,8+35,7+32,9)/3 =35,8
уср.15 = (35,7+32,9+34,3)/3 =34,3
уср. 16 = (32,9+34,3+50,9)/3 =39,37
уср.17 = (34,3+50,9+41,3)/3 =42,17
уср.18 = (50,9+41,3+43,7)/3 =45,3
уср.19 = (41,3+43,7+36,5)/3 =40,5
уср.20 = (43,7+36,5+40,3)/3 =40,17
уср.21 = (36,5+40,3+40,7)/3 =39,17
уср.22 = (40,3+40,7+42,2)/3 =41,07
уср.23 = (40,7+42,2+39)/3 =40,63
Таблица 30
| Время | Прибыль | Экспоненциальное сглаживание | у 3ур. |
| 1 кв.2005 | 45,1 | 36,08 | - |
| 2 кв.2005 | 42,7 | 42,77 | 43,07 |
| 3 кв.2005 | 41,4 | 41,17 | 40,23 |
| 4кв.2005 | 36,6 | 37,39 | 40,57 |
| 1кв.2006 | 43,7 | 43,63 | 43,33 |
| 2кв. 2006 | 44,9 | 44,65 | 43,67 |
| 3кв.2006 | 42,4 | 42,11 | 40,97 |
| 4кв.2006 | 35,6 | 37,02 | 42,7 |
| 1кв. 2007 | 50,1 | 49,45 | 46,83 |
| 2кв2007 | 54,8 | 54,13 | 51,43 |
| 3кв.2007 | 49,4 | 49,39 | 49,33 |
| 4кв.2007 | 43,8 | 43,84 | |
| 1кв.2008 | 38,8 | 38,93 | 39,43 |
| 2кв.2008 | 35,7 | 35,72 | 35,8 |
| 3кв.2008 | 32,9 | 33,18 | 34,3 |
| 4кв2008 | 34,3 | 35,31 | 39,37 |
| 1кв.2009 | 50,9 | 49,15 | 42,17 |
| 2кв.2009 | 41,3 | 42,10 | 45,3 |
| 3кв.2009 | 43,7 | 43,06 | 40,5 |
| 4кв.2009 | 36,5 | 37,23 | 40,17 |
| 1кв.2010 | 40,3 | 40,07 | 39,17 |
| 2кв.2010 | 40,7 | 40,77 | 41,07 |
| 3кв.2010 | 42,2 | 41,89 | 40,63 |
| 4кв.2010 | 31,20 | - |
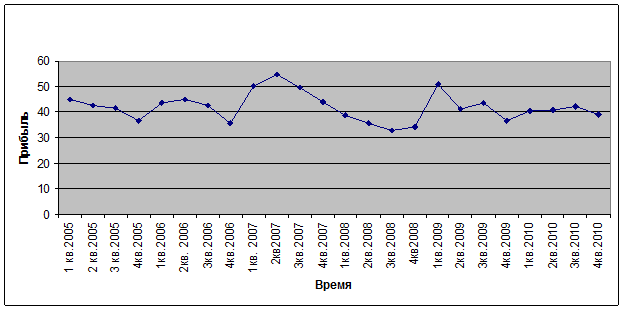
Рис.7
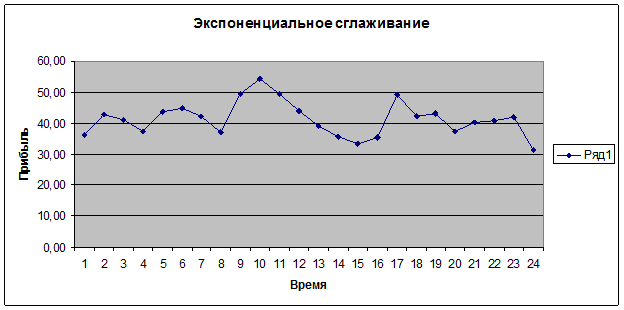
Рис.8
8. Анализ взаимосвязи между динамическими рядами (корреляция приростов, отклонений от тренда)
Для этого нам понадобятся данные двух показателей выручки и чистой прибыли. Выручка – факторный признак, а чистая прибыль – результативный признак.
Чтобы провести данный анализ необходимо пройти 3 этапа статистического анализа корреляционной связи:
I ЭТАП. Предварительный анализ (выявление наличия связи);
II ЭТАП. Корреляционный анализ (установление силы и направления связи);
III ЭТАП. Регрессионный анализ (определение математической модели связи).
Виды корреляционной связи:
I По силе бывает
- прямая – увеличение факторного признака приводит к росту результативного;
- обратная – увеличение факторного признака приводит к уменьшению результативного.
II По направлению бывает
- слабая (до 10% вариации). Когда факторный признак объясняет до 10 % вариации результативного;
- умеренная (от 10-25% вариации);
- средняя (от 25 – 50% вариации);
- сильная (более 50% вариации).
III По числу факторных признаков бывает
- парная. Когда влияет только 1 фактор на результативность;
- множественная. Когда несколько факторов влияют на результативность, и оцениваем совместное влияние всех.
IV По характеру аналитической зависимости бывает
- линейная. Когда наилучшим образом для описания связи подходит линейная математическая модель;
- не линейная. Когда характер связи будет явно нелинейным.
I. Выявление наличия связи графическим способом.
Таблица 31
| Время | Выручка(x) | Прибыль(y) |
| 1 кв.2005 | 45,1 | |
| 2 кв.2005 | 168,2 | 42,7 |
| 3 кв.2005 | 166,6 | 41,4 |
| 4кв.2005 | 36,6 | |
| 1кв.2006 | 178,3 | 43,7 |
| 2кв. 2006 | 180,7 | 44,9 |
| 3кв.2006 | 178,1 | 42,4 |
| 4кв.2006 | 174,1 | 35,6 |
| 1кв. 2007 | 50,1 | |
| 2кв2007 | 208,2 | 54,8 |
| 3кв.2007 | 203,5 | 49,4 |
| 4кв.2007 | 197,5 | 43,8 |
| 1кв.2008 | 38,8 | |
| 2кв.2008 | 221,3 | 35,7 |
| 3кв.2008 | 218,1 | 32,9 |
| 4кв2008 | 34,3 | |
| 1кв.2009 | 226,5 | 50,9 |
| 2кв.2009 | 215,9 | 41,3 |
| 3кв.2009 | 218,4 | 43,7 |
| 4кв.2009 | 218,7 | 36,5 |
| 1кв.2010 | 40,3 | |
| 2кв.2010 | 232,8 | 40,7 |
| 3кв.2010 | 235,2 | 42,2 |
| 4кв.2010 |
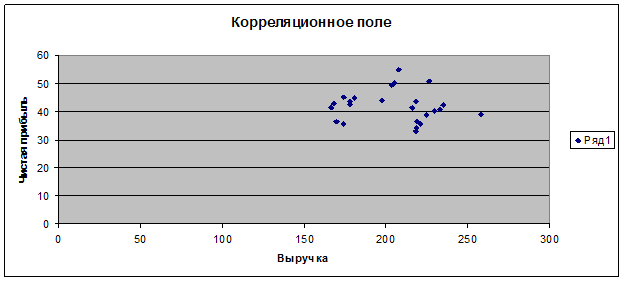
Рис.9
Вывод: Можно говорить об отсутствии линейной связи между признаками. Так как между точками на графике мы не можем визуально провести прямую линию.