Лекция 1. переходные процессы в электрических цепях

Включение и выключение источников и приемников электроэнергии, возникновение коротких замыканий и т. п. связано с мгновенным изме­нением параметров электрических цепей и сопровождается протеканием в них переходных электромагнитных процессов. Переходным называется процесс, возникающий в любой системе при переходе от одного устано­вившегося процесса (режима) к другому. Электромагнитные переходные процессы занимают обычно относительно небольшое время (от долей до нескольких секунд), но сопровождаются „бросками" токов, „провалами" или „всплесками" напряжений, которые могут вызвать срабатывание за­щитных устройств, повреждение деталей, чрезмерные перегревы, пробой изоляции и др.

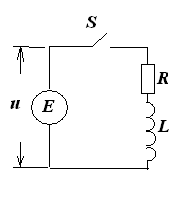
Рис. 1.1. Схема электрической цепи с обобщенными парамет­рами при подключении к ис­точнику электроэнергии

При подключении r –L цепи выключателем S источнику постоянного тока возникает переходный процесс между начальным установившимся режимом работы, соответствующим i= 0и конечным установившимся режимом, соответствую­щим току i= i_уст. Изменение тока в цепи от 0 до i_уст за время переходного процесса связано с изменением магнитного потока катушки и возникно­вением в ней ЭДС самоиндукции е _L = - L (di/dt). На основании второго закона Кирхгофа (сумма напряжений и ЭДС в замкнутом контуре равна сумме падений напряжений) применительно к схеме на рис. 1.1 можно составить следующее уравнение:

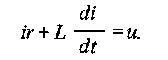(1.1)

Уравнение (1.1) называется линейным дифференциальным уравне­нием первого порядка. Полное решение данного уравнения относительно тока находится как сумма токов двух частных решений, т. е.

i= i+ i_св (1.2)

Значение тока первого частного решения 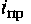соответствует установив­шемуся процессу, который наступает в цепи после окончания переходного процесса. Данный ток принято называть принужденным (или установив­шимся) , поскольку он течет под действием напряжения источника элект­роэнергии. Значение принужденного тока находится из уравнения (1.1), написанного для установившегося режима, т. е.

i_прr + L di_пр/dt = u (1.3)

Поскольку i_пр=const, di_пр/dt=0, Следовательно, i_пр r = u или i_пр = u / r ( 1.4)

Формула (1.4) соответствует закону Ома для электрической цепи постоянного тока. Значение тока второго частного решения i_свсоответ­ствует .свободному процессу изменения тока при отсутствии в цепи источ­ника электроэнергии (при закороченном источнике) под действием запасенной в цепи энергии. Данный ток принято называть свободным. Значение свободного тока находится из уравнения (1.1) при u=0, т.е.

i_свr + L di_св/dt = 0 (1.5)

Решение данного дифференциального уравнения можно представить в сле­дующем виде:

i_{св =} А е ^{- αt} (1.6)

где А — постоянная интегрирования; е — основание натуральных логариф­мов (е = 2,72); α — корень характеристического уравнения.

Постоянная интегрирования А определяется уравнением (1.2) для на­чальных условий t= 0, i=0

Поскольку любое число в нулевой степени равно 1, имеем 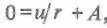откуда

A=u/ r (1.7)

Дифференциальному уравнению (8.5) соответствует следующее ха­рактеристическое уравнение:

r +La =0

откуда корень уравнения a = r/L(1.8)

Объединив формулы (8.6) — (8.8), получим

i_св= (- u/r) е ^{– r/Lt}

Обычно данную формулу принято записывать в виде

i_св= (- u/r) е ^{–τ/ t} (1.9)

где τ — постоянная времени электрической цепи L/r , с.

Из формул (1.4) и (1.9) следует, что принужденный ток имеет по­стоянное значение, а свободный ток является затухающим. Процесс зату­хания свободного тока определяется множителем 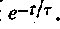Объединив формулы (1.2), (1.4) и 1.9), получим полное решение уравнения (1.1) в виде

( i=u/r – (u/r) е^–τ/t = u/r( 1- е^–τ/t)(1.12)

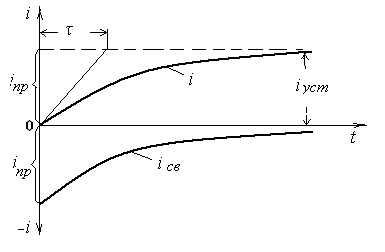
Рис. 1.2. График изменения токов при подключении электрической цепи к источнику постоянного тока

На рис. 1.2 представлен график изменения принужденного, свободного и общего (результирующего) то­ков, построенных на основании формул (1.4), (1.9) и (1.12) или (1.2). Из графика видно, что значения принужденного и свободного токов распо­ложены в первом и четвертом квадрантах, ординаты которых имеют про­тивоположное направление. При t=0 значения принужденного и свободного токов равны, но противоположны по направлению, поэтому значение общего тока равно нулю. По мере уменьшения свободного тока происходит нарастание общего тока. Приi_св=0 значение общего тока достигает значения принужденного (установившегося) токаi_уст.Нарастание общего тока происходит по кривой, подобной кривой затухания свободного тока. Если через начало коорди­нат провести касательную к кривой общего тока, то она, пересекая линию принужденного тока, отсечет отрезок, равный постоянной времени т. Из графика ясно, что длительность переходного процесса пропорцио­нальна значению т, а следовательно отношению L/ r. При L>r переходный процесс затягивается, при L< r — быстро затухает.

При подключении электрической цепи (см. рис. 1.1) к источнику си­нусоидального переменного тока напряжением u = (U_{max / Z}) sin (wt+α – φ) урав­нение переходного процесса (8.1) и методика его решения полностью со­храняются. Однако значения принужденного, свободного и общего токов при этом будут определяться другими формулами. Значение принужден­ного (установившегося) тока по аналогии с формулой (1,4) определяется законом Ома для электрической цепи переменного тока, состоящей из активного сопротивления r и индуктивного сопротивления х =wt, т. е.

i = (U_{max / Z} ) sin (wt+α – φ) = I _max sin (wt+α – φ) (1.13)

где:

I _max =U_{max / Z}

Z = √г2 + х2 — полное, активное и реактивное сопротивления электрической

цепи; а — угол, определяющий, напряжение в момент включения при t=0; φ - сдвиг фаз (угол между векторами) тока и напряжения;I_mах - амплитудное значение тока.

Свободный ток при t=0 равен по значению и противоположен по направлению принужденному току, т. е,

! i_св! _t=0 = ! i _пр! _t=0 = - I _max sin (α – φ)(1.14)

Затем данный ток затухает по экспоненциальной кривой, что определяется множителем е ^–τ/t. Формула свободного тока в этом случае будет иметь вид:

i_св= - - I _max sin (α – φ) е^–τ/t(1.15)

где τ= L/r = х/wг - постоянная времени электрической цепи.

Общий ток переходного процесса определяется формулой

i = i _пр+ i_св= I _max [sin (wt+α – φ) - sin (α – φ) е^–τ/t](1.16)

Из формулы (1.13) следует, что принужденный ток изменяется по синусоидальному закону, имеет периодический характер и его называют периодическим током. Характер изменения свободного тока, согласно (1.15), является затухающим и непериодическим, поэтому его принято называть апериодическим.

Анализ формул (1.13), (1.15) и (1.16) дает возможность убедиться, что наибольшие мгновенные значения токов переходного процесса соот­ветствуют включению цепи в момент прохождения напряжения через ну­левое значение (при а = 0), а также при φ = - 90⁰,т. е. пренебрегая актив­ным сопротивлением цепи (практически при x >r). Тогда

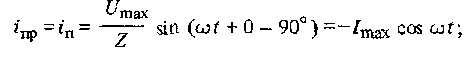(1.17)

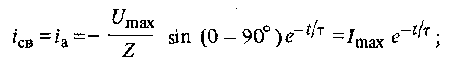(1.18)

i = i_пр + i_св = -I _max cosωt + I _max e^-t/τ (1.19)

На рис. 1.3 представлен график изменения токов, построенных на ос­новании формул (1.17) - (1.19). Из графика видно, что при I = 0 значе­ния периодического и апериодического токов равны I_max,, но противопо­ложны по знаку (направлению). Апериодический ток i_а расположенный в первом квадранте, затухает до нуля, не изменяя своего направления. Периодический ток i_пр изменяется по синусоидальной (косинусоидальной) кривой с неизменным значением амплитуды 1_тзх.

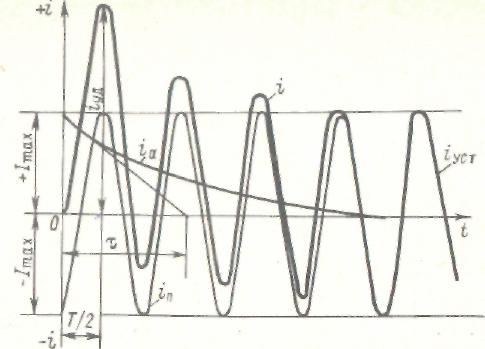Рис. 1.3. График изменения токов при подключении элек­трической цепи к источнику переменного тока

Через половину периода изменения периодического тока, т. е. при wt= л = Т/2 и t = 1/2f = 0,01 с, амплитуды периодического и апериодиче­ского токов, имея одинаковое направление, дают наибольшее суммарное значение общего тока, которое принято называть ударным током. Значе­ние ударного тока определяется формулой (1.19) при соs π = -1 и τ = 0,01 с

i_уд = I_mах + I_mах e ^{-0/01/ τ} = I_max (1 + e ^{-0/01/ τ} ) (1.20)

Обозначив К_уд = (1 + e ^{-0/01/ τ} ), получим: i_уд = К_уд I_max

Из формулы следует, что значение ударного коэффициента из­меняется в пределах от 1 до 2 в зависимости от изменения τ в пределах от 0 до ∞ (τ= 0 при х = 0; τ= ∞ при r= 0). В первом случае свободный ток равен нулю, во втором — свободный ток не затухает.

Практически при х>r переходный процесс растягивается, а значение ударного коэффициента приближается к 2; при r > х процесс быстро за­тухает, а значение коэффициента приближается к 1.

Возникновение короткого замыкания, например между точками а и б схемы на рис. 1.4, связано с мгновенным образованием замкнутой электрической цепи и появлением в ней тока i_к.з , что аналогично подключению переключателем приемника к источнику электроэнергии. Переходный процесс подключения электрической цепи к источнику совпадает с переходным процессом короткого замыкания и описывается формулами (1.1 -1.22).

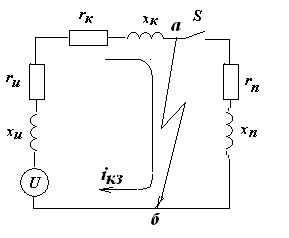
Рис.1.4 Схема электрической сети при возникновении короткого замыкания в кабеле.

Вместе с тем следует заметить, что указанные формулы получены на основе постоянных значений э.д.с. и напряжения источника питания и постоянных значений активных и реактивных сопротивлений электрической цепи. На практике, при рассмотрении переходных процессов, значения э.д.с. и внутренние сопротивления источников питания ( генераторов) и приемников (двигателей) могут изменяться. Поэтому параметры x_и и r_и источников и x_п и r_п приемников на схемах обычно разделяют.

Контрольные вопросы

1.Назовите причины возникновения переходных процессов в энергосистемах.

2.Напишите уравнение переходного процесса при подключении простой R-L цепи к источнику постоянного напряжения.

3. Как определить принужденный ( установившийся) и свободный ток в этой цепи? Что является причиной появления свободного тока в цепи?

4.Напишите уравнение переходного процесса при подключении простой R-L цепи к источнику переменного напряжения.

5.Как определить периодический ток и апериодический ( свободный) ток в этой цепи. Условия подключения цепи , при которых имеет место максимальные значения апериодических токов.

6 Что такое ударный ток и как его определить?

7. Каковы особенности переходного процесса, соответствующие режиму короткого замыкания в цепи переменного ток?