Множества, операции над ними. Функция, график функции. Классы функций
СОДЕРЖАНИЕ
Практическое занятие 1.Множества, операции над ними. Функция, график функции. Классы функций……….…………………………......................……5
Практическое занятие 2.Последовательность и ее предел. Монотонная последовательность. Число «е». Раскрытие неопределенностей. Бесконечные пределы…………..……………………..…………………………………………7 Практическое занятие 3.Предел функции. Бесконечно малые и бесконечно большие……………………………………………………….…………………..9 Практическое занятие 4.Первый замечательный предел …………………12
Практическое занятие 5, 6.Непрерывность функции в точке. Локальные свойства непрерывной функции. Точки разрыва. Глобальные свойства непрерывных функций………………………………………………….…….....13
Практическое занятие 7.Производная. Геометрический, механический смысл. Техника дифференцирования. Производная сложной функции……17
Практическое занятие 8.Логарифмическое дифференцирование.
Производная параметрически заданной функции, неявной функции……...20
Практическое занятие 9.Дифференциал. Основные правила дифференцирования. Применение дифференциала в приближенных вычислениях…………………………………………………………………….24
Практическое занятие 10.Производные высших порядков. Формула Лейбница. Правило Лопиталя и вычисление пределов……………..………..26
Практическое занятие 11.Монотонность, экстремумы функции………...27
Практическое занятие 12.Выпуклость, вогнутость, точки перегиба. Асимптоты. Построение графиков функций……….………………………….29
Практическое занятие 13.Формула Тейлора и ее использование в приближенных вычислениях ……………………………….………………….31
Практическое занятие 14Первообразная. Методы интегрирования разложением…………………………………….……………………………….34 Практическое занятие 15.Методы замены переменных, интегрирования по частям ………………………….………………………………..……………….36
Практическое занятие 16.Интегрирование простейших рациональных дробей. Интегрирование некоторых иррациональностей ……..…………….38
Рекомендуемая литература………………….…………………………….…42
Практическое занятие №1
Множества, операции над ними. Функция, график функции. Классы функций
Пересечением множества А и В называется новое множество С, содержащее те и только те элементы, которые входят в оба множества А и В.
Пересечение множеств называется также их произведением. Обозначают Х = АÇВ или Х= А×В.
Задача 1. Найти пересечение множеств А = {2,3,7,8,10}, В = {1,3,5,6,8,9}.
Решение. Пересечением будет множество С=АÇВ = {3,8}.
Объединением множеств А и В называется множество С, состоящее из тех и только тех элементов, которые входят хотя бы в одно из этих множеств. Объединение множеств называется также суммой.
Обозначают так: С= АÈВ или С= А + В.
Задача 2. Найти объединение множеств А={1;7;5}, В={1;3;17}.
Решение. Объединением множеств будет С=А 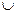 В={1;3;7;5;17}.
В={1;3;7;5;17}.
Разностью двух множеств А и В называется такое множество С= А\В, в которое входят все элементы из А, не принадлежащие множеству В.
Множество M называется областью определения функции. Очень часто при задании функции область определения этой функции не указывается. В таком случае под областью определения функции понимают область существования аналитического выражения y=f(x), т. е. множество значений аргумента x для которых аналитическое выражение имеет определенное конечное значение.
Задача 3. Найти область определения функции 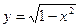 .
.
Решение. Даная функция существует, если 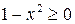 . Решением этого неравенства будет отрезок [-1;1], значит функция определена на отрезке [-1;1].
. Решением этого неравенства будет отрезок [-1;1], значит функция определена на отрезке [-1;1].
Задача 4. Найти область определения функций:
4.1 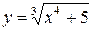 1.16
1.16 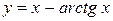
4.2 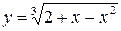 4.17
4.17 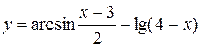
4.3 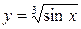 4.18
4.18 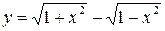
4.4 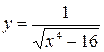 4.19
4.19 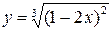
4.5 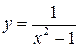 4.20
4.20 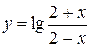
4.6 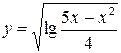 4.21
4.21 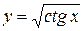
4.7 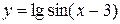 4.22
4.22 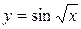
4.8 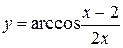 4.23
4.23 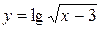
4.9 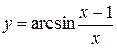 4.24
4.24 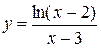
4.10 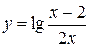 4.25
4.25 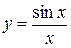
4.11 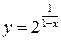 4.26
4.26 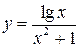
4.12 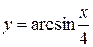 4.27
4.27 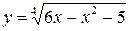
4.13 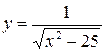 4.28
4.28 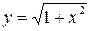
4.14 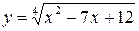 4.29
4.29 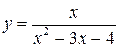
4.15 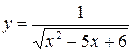 4.30
4.30 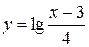
Практическое занятие №2
