Доказательство. Представим результат опыта как УУН НУ (один из вариантов)

Представим результат опыта как УУН…НУ (один из вариантов). Количество У - равно .

События У и Н - независимы , поэтому

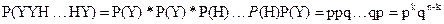
Cколько может быть таких вариантов?

У

У

У

У

У

Сколькими способами в местах (ячеек, испытаний) можно занять мест (поставить фишки и т. д.)? - С_n^k

Например - 3 успеха в 4 испытаниях -С₄³

НУУУ

УНУУ

УУНУ

УУУН

Эти события несовместны, т.к. не могут произойти одновременно, поэтому вероятность их объединения равна сумме их вероятностей.

.<

Следствия:

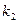1. Вероятность появления события А в испытаниях не более раз и не меньше раз:

P_n(k₁ ≤ k ≤ k₂) = 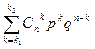-т.к. события при разных являются несовместными.

2. Вероятность появления А хотя бы один раз в 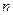испытаниях.

P_n(k ≥ 1) = 1 – qⁿ = 1- P_n(k=0) = 1- C_n⁰p⁰qⁿ=1-qⁿ

V В семье 10 детей. Считая вероятность рождения мальчика равной 0.5, определить:

a. Вероятность того, что в семье ровно 5 мальчиков;

b. Вероятность того, что в семье не более 5 мальчиков;

c. Вероятность того, что в семье хотя бы 1 мальчик.

Ï а) Р₁₀(к=5) = С₁₀⁵(1/2)⁵(1/2)⁵ = 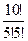(1/2)¹⁰≈0,246;

b) Р₁₀(0≤ к≤ 5) = 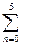С₁₀^к(1/2)ⁿ(1/2)^n-k = (С₁₀⁰+С₁₀¹ +С₁₀² +С₁₀³ +С₁₀⁴+С₁₀⁵)/1024 ≈0.623;

c) Р₁₀(k≥1) = 1 – (½)¹⁰ = 1-1/1024 = 1023/1024 ≈ 0.999. N

V В течение 6 дней ведутся ремонтные работы водопровода. Вероятность того, что вода будет отключена на сутки 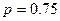и не зависит от хода ремонтных работ. Определить вероятность того, что в течение этой злосчастной недели ровно 4 суток не будет воды.

Ï Р₆(к=4) = С₆⁴ 0.75⁴ 0.25² = 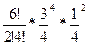≈0.3. N

Якоб Бернулли

1654-1705

Швейцарский математик.

Наиболее значительны достижения в развитии анализа бесконечно малых, теории рядов, вариационного исчислении и теории вероятностей. Благодаря его работам теория вероятностей приобрела важнейшее значение в практической деятельности.