Требования к оформлению контрольной работы 5 страница

По найденному значению φ построим векторную диаграмму (рис. 14).

Пример 22. Материальная точка массой m=5 г совершает гармонические колебания с частотой ν =0,5 Гц. Амплитуда колебаний A=3 см. Определить: 1) скорость v точки в момент времени, когда смещение х= 1,5 см; 2) максимальную силу F_max, действующую на точку; 3) полную энергию 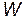колеблющейся точки.

Решение. 1. Уравнение гармонического колебания имеет вид:

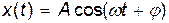, (1)

а формулу скорости получим, взяв первую производную по времени от смещения:

(2)

Чтобы выразить скорость через смещение, надо исключить из формул (1) и (2) время. Для этого возведем оба уравнения в квадрат, разделим первое на , второе на и сложим:

или .

Решив последнее уравнение относительно 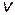, найдем

.

Выполнив вычисления по этой формуле, получим

см/с.

Знак плюс соответствует случаю, когда направление скорости совпадает с положительным направлением оси х, знак минус — когда направление скорости совпадает с отрицательным направлением оси х.

Смещение при гармоническом колебании кроме уравнения (1) может быть определено также уравнением:

.

Повторив с этим уравнением такое же решение, получим тот же ответ.

2. Силу, действующую на точку, найдем по второму закону Ньютона:

(3)

где а — ускорение точки, которое получим, взяв производную по времени от скорости:

, или

Подставив выражение ускорения в формулу (3), получим:

.

Отсюда максимальное значение силы:

.

Подставив в это уравнение значения величин π, ν, m и A, найдем:

мН.

3. Полная энергия колеблющейся точки есть сумма кинетической и потенциальной энергий, вычисленных для любого момента времени.

Проще всего вычислить полную энергию в момент, когда кинетическая энергия достигает максимального значения. В этот момент потенциальная энергия равна нулю. Поэтому полная энергия 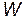колеблющейся точки равна максимальной кинетической энергии 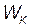_max:

(4)

Максимальную скорость определим из формулы (2), положив ; . Подставив выражение скорости в формулу (4), найдем

Подставив значения величин в эту формулу и произведя вычисления, получим

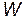Дж = 22,1·10^-6Дж или =22,1 мкДж.

Пример 23. На концах тонкого стержня длиной l = 1 м и массой m₃=400 г укреплены шарики малых размеров массами m₁=200 г и m₂=300г. Стержень колеблется около горизонтальной оси, перпендикулярной стержню и проходящей через его середину (точка О на рис. 15). Определить период Т колебаний, совершаемых стержнем.

Решение. Период колебаний физического маятника, каким является стержень с шариками, определяется соотношением

(1)

где J — момент инерции маятника относительно оси колебаний; m – его масса; l_С — расстояние от центра масс маятника до оси.

Момент инерции данного маятника равен сумме моментов инерции шариков J₁ и J₂ и стержня J₃:

(2)

Принимая шарики за материальные точки, выразим моменты их инерции: ; .

Так как ось проходит через середину стержня, то его момент инерции относительно этой оси . Подставив полученные выражения J₁ , J₂ и J₃ в формулу (2), найдем общий момент инерции физического маятника:

.

Произведя вычисления по этой формуле, найдем кг·м².

Масса маятника состоит из масс шариков и массы стержня:

=0,9 кг.

Расстояние l_С центра масс маятника от оси колебаний найдем, исходя из следующих соображений. Если ось х направить вдоль стержня и начало координат совместить с точкой О, то искомое расстояние l равно координате центра масс маятника, т. е.

.

Подставив значения величин m₁, m₂, m, l и произведя вычисления, найдем:

см.

Произведя расчеты по формуле (1), получим период колебаний физического маятника:

с = 11,2 с.

Пример 24.Складываются два колебания одинакового направления, выражаемых уравнениями ; , где А₁=1см, A₂=2 см, с, с, ω = 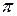с^-1. 1. Определить начальные фазы φ₁ и φ₂ составляющих колебаний. 2. Найти амплитуду А и начальную фазу φ результирующего колебания. Написать уравнение результирующего колебания.

Решение. 1. Уравнение гармонического колебания имеет вид

(1)

Преобразуем уравнения, заданные в условии задачи, к такому же виду:

, (2)

Из сравнения выражений (2) с равенством (1) находим начальные фазы первого и второго колебаний:

рад и рад.

2. Для определения амплитуды А результирующего колебания удобно воспользоваться векторной диаграммой, представленной на рис. 16. Согласно теореме косинусов, получим

, (3)

где — разность фаз составляющих колебаний. Так как , то, подставляя найденные значения φ₂ и φ₁ получим рад.

Подставим значения А₁ , А₂и в формулу (3) и произведем вычисления:

A=2,65 см.

Тангенс начальной фазы φ результирующего колебания определим непосредственно из рис. 16: , откуда начальная фаза

.

Подставим значения А₁, А₂, φ₁, φ₂ и произведем вычисления:

рад.

Так как угловые частоты складываемых колебаний одинаковы, то результирующее колебание будет иметь ту же частоту ω. Это позволяет написать уравнение результирующего колебания в виде , где A=2,65 см, ω = 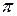с^-1, рад.

Пример 25.Материальная точка участвует одновременно в двух взаимно перпендикулярных гармонических колебаниях, уравнения которых

, (1)

, (2)

где А₁=1 см, A₂=2 см, ω = 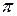с^-1. Найти уравнение траектории точки. Построить траекторию с соблюдением масштаба и указать направление движения точки.

Решение. Чтобы найти уравнение траектории точки, исключим время t из заданных уравнений (1) и (2). Для этого воспользуемся формулой . В данном случае , поэтому

Так как согласно формуле (1) , то уравнение траектории

(3)

Полученное выражение представляет собой уравнение параболы, ось которой совпадает с осью Ох. Из уравнений (1) и (2) следует, что смещение точки по осям координат ограничено и заключено в пределах от – 1 до +1 см по оси Ох и от – 2 до +2 см по оси Оу.

Для построения траектории найдем по уравнению (3) значения у, соответствующие ряду значений х, удовлетворяющих условию см, и составим таблицу:

x,см	– 1	– 0,75	– 0,5		+0,5	+ 1
у,см		±0,707	±1	±1,41	±1,73	±2

Начертив координатные оси и выбрав масштаб, нанесем на плоскость хОу найденные точки. Соединив их плавной кривой, получим траекторию точки, совершающей колебания в соответствии с уравнениями движения (1) и (2) (рис. 17).

Для того чтобы указать направление движения точки, проследим за тем, как изменяется ее положение с течением времени. В начальный момент t=0 координаты точки равны x(0)=1 см и y(0)=2 см. В последующий момент времени, например при t₁=l с, координаты точек изменятся и станут равными х(1)= – 1 см, y(1)=0. Зная положения точек в начальный и последующий (близкий) моменты времени, можно указать направление движения точки по траектории. На рис. 17 это направление движения указано стрелкой (от точки А к началу координат). После того как в момент t₂ = 2 с колеблющаяся точка достигнет точки D, она будет двигаться в обратном направлении.

Пример 26. Космический корабль движется со скоростью 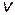=0,9с по направлению к центру Земли. Какое расстояние l пройдет этот корабль в системе отсчета, связанной с Землей (K-система), за интервал времени Δt₀=1 с, отсчитанный по часам, находящимся в космическом корабле (K'-система)? Суточным вращением Земли и ее орбитальным движением вокруг Солнца пренебречь.

Решение. Расстояние l, которое пройдет космический корабль в системе отсчета, связанной с Землей (K-система), определим по формуле

(1)

где — интервал времени, отсчитанный в K-системе отсчета. Этот интервал времени связан с интервалом времени, отсчитанным в K'-системе, соотношением .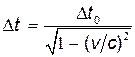

Подставив выражение в формулу (1), получим:

После вычислений найдем:

l=619 Мм.

Пример 27.В лабораторной системе отсчета (K-система) движется стержень со скоростью 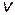=0,8с.По измерениям, произведенным в K-системе, его длина l оказалась равной 10 м, а угол φ, который он составляет с осью х, оказался равным 30° . Определить собственную длину l₀ стержня в K'-системе, связанной со стержнем, и угол φ₀, который он составляет с осью х' (рис. 18)

Решение. Пусть в K'-системе стержень лежит в плоскости х'О'у'. Из (рис. 18, а) следует, что собственная длина l₀ стержня и угол φ₀, который он составляет с осью х', выразятся равенствами

(1)

В K-системе те же величины окажутся равными (рис. 18, б)

(2)

Заметим, что при переходе от системы К' к К размеры стержня в направлении оси у не изменятся, а в направлении оси х претерпят релятивистское (лоренцево) сокращение, т. е.

, (3)

С учетом последних соотношений собственная длина стержня выразится равенством

или

Заменив в этом выражении на (рис. 18, б), получим

Подставив значения величин в это выражение и произведя вычисления, найдем

l₀=15,3 м.

Для определения угла воспользуемся соотношениями (1), (2) и (3):

, или

откуда

.

Подставив значения φ и β в это выражение и произведя вычисления, получим

.

Пример 28.Кинетическая энергия Т электрона равна 1 МэВ. Определить скорость электрона.

Решение. Релятивистская формула кинетической энергии

Выполнив относительно β преобразования, найдем скорость частицы, выраженную в долях скорости света ( ):

(1)

где E₀= =0,511 МэВ — энергия покоя электрона.

Вычисления по этой формуле можно производить в любых единицах энергии, так как наименования единиц в правой части формул сократятся и в результате подсчета будет получено отвлеченное число.

Подставив числовые значения Е₀и Т в мегаэлектрон-вольтах, получим

β=0,941.

Так как , то

м/с.

Чтобы определить, является ли частица с кинетической энергией Т релятивистской или классической, достаточно сравнить кинетическую энергию частицы с ее энергией покоя.

Если , частицу можно считать классической. В этом случае релятивистская формула (1) переходит в классическую:

, или .

Пример 29. Определить релятивистский импульс р и кинетическую энергию Т электрона, движущегося со скоростью (где с — скорость света в вакууме).

Решение. Релятивистский импульс

(1)

После вычисления по формуле (1) получим

кг·м/с.

В релятивистской механике кинетическая энергия Т частицы

. (2)

Сделав вычисления, найдем

T=106 фДж.

Во внесистемных единицах энергия покоя электрона =0,511 МэВ. Подставив это значение в формулу (2), получим

Т=0,66 МэВ.

Пример 30.Релятивистская частица с кинетической энергией (m – масса частицы) испытывает неупругое столкновение с такой же покоящейся (в лабораторной системе отсчета) частицей. При этом образуется составная частица. Определить: 1) массу составной частицы; 2) ее кинетическую энергию Т'.

Решение. 1. Для того чтобы найти массу составной частицы, воспользуемся инвариантностью величины

. (1)

До столкновения (в лабораторной системе отсчета):

полная энергия частиц ,

импульс частиц ,

.

После столкновения (в системе отсчета связанной с составной частицей):

энергия и импульс составной частицы ,

.

В силу инвариантности величины (1) .

Тогда масса составной частицы:

.

2. Скорость составной частицы (равна скорости центра масс частиц до столкновения) .

Кинетическая энергия составной релятивистской частицы:

.

Таблица вариантов

Контрольная работа № 1

Вариант	Номера задач

Задачи

1. Два тела бросили одновременно из одной точки: одно – вертикально вверх, другое – под углом 60⁰ к горизонту. Начальная скорость каждого тела 25 м/с. Пренебрегая сопротивлением воздуха, найти расстояние между телами через 1,7 с.

2. Две частицы движутся с ускорением g в однородном поле силы тяжести. В начальный момент частицы находились в одной точке и имели скорости 3 м/с и 4 м/с, направленные горизонтально и в противоположные стороны. Найти расстояние между частицами в момент, когда векторы их скоростей окажутся взаимно перпендикулярными.

3. Кабина лифта, у которой расстояние от пола до потолка равно 2,7 м, начала подниматься с постоянным ускорением 1,2 м/с². Через 2 с после начала подъема с потолка кабины стал падать болт. Найти: а) время свободного падения болта; б) перемещение и путь болта за время свободного падения в системе отсчета, связанной с шахтой лифта.

4. В момент времени t=0 частица вышла из начала координат в противоположном направлении оси x. Ее скорость меняется по закону , где - вектор начальной скорости, модуль которого см/с, Т=5 с. Найти: а) координату х частицы в моменты времени 6 с, 10 с и 20 с; б) момент времени, когда частица будет находиться на расстоянии 10 см от начала координат; в) путь S, пройденный частицей за первые 4 и 8 с; изобразить примерный график S(t).

5. Материальная точка движется прямолинейно с ускорением а=5 м/с². Определить на сколько путь, пройденный точкой в n-ю секунду, будет больше пути, пройденного в предыдущую секунду. Принять .

6. Велосипедист ехал из одного пункта в другой. Первую треть пути он проехал со скоростью км/ч. Далее половину оставшегося времени он ехал со скоростью км/ч, после чего до конечного пункта он шел пешком со скоростью км/ч. Определить среднюю скорость велосипедиста.

7. Тело брошено с начальной скоростью с высоты h=2,4 м вверх под углом =35⁰ к горизонту и упало на расстоянии l=37 м от места бросания. Найти начальную скорость тела.

8. Тело брошено с вышки в горизонтальном направлении со скоростью 20 м/с. Определить скорость тела и ее направление в конце второй секунды после начала движения.

9. Твердое тело вращается вокруг неподвижной оси по закону , где а=6 рад/с, b=2 рад/с³. Найти: а)средние значения угловой скорости и углового ускорения за промежуток времени от начала вращения до остановки; б) угловое ускорение в момент остановки тела.

10. Точка движется по окружности радиусом R= 30 см с постоянным угловым ускорением. Определить тангенциальное ускорение точки, если известно, что за время 4 с она совершила три оборота и в конце третьего оборота ее нормальное ускорение =2,7 м/с².