Структурно-параметрическое описание и назначение

Параметров объекта

Применение вычислительной техники и математических методов при проектировании сложных технических систем возможно только в том случае, если имеются их адекватные математические модели. Возможность построения иерархии моделей играет важную роль в процессе автоматизированного проектирования и создания САПР. В математической модели проектируемо- го объекта выделяют структурно-параметрическое описание собственно объекта и описание поведения объекта во времени и внешней среде. Таким образом, математическая модель проектируемого объекта состоит из двух частей: структурно-параметрического описания объекта с помощью набора проектных параметров и модели функционирования.

Под структурно-параметрическим описанием ОУ будем понимать та- кое его описание, которое показывает, из каких подсистем, блоков, агрегатов, деталей состоит данный объект, как эти компоненты соединены и взаимодействуют между собой, каковы их весовые, габаритные характеристики и т.д. Структурно-параметрическое описание должно давать возможность генерировать множество альтернатив ОУ, быть достаточно подробным, соответствующим этапу проектирования и доставлять информацию для моделей функционирования.

Для сложных объектов существуют различные методы структурно- параметрического описания ОУ: систематического покрытия поля, отрицания и конструирования, морфологического ящика, комбинаторного файла и т.д.

При построении модели наряду со структурным возникает потребность в параметрическом описании ОУ. Обычно такое описание дается конечным набором параметров, варьируя значения которых в определенных пределах с учетом необходимых ограничений, можно вводить в структуру ОУ различные по характеристикам подсистемы.

Параметрическое описание объекта включает в себя выделение совокупности входных переменных (внешних параметров) Х₁, Х₂, …, Х_n, управляющих воздействий U₁, U₂, …, U_k, влияющих на процесс, выходных переменных (зависимых параметров) Y₁, Y₂, …, Y_m, характеризующих протекание процесса, а также внутренних параметров модели P₁, P₂, …, P_l.

Управляющие воздействия U₁, U₂, …, U_k являются целенаправленно изменяемыми переменными и формируются на основе информации о входных переменных, которые называются управляемыми. Остальные входные переменные относятся к возмущающим воздействиям, а выходные переменные.

Внутренние параметры модели – это внутренние характеристики объекта, не зависящие от процесса моделирования, например, конструктивные параметры агрегатов, теплофизические свойства объектов и т.п.

Возмущающие воздействия и неуправляемые переменные могут быть контролируемыми (наблюдаемыми) и неконтролируемыми (ненаблюдаемыми).

В математическом моделировании используется различный математический аппарат в зависимости от характера моделируемого процесса или объекта.

Модели функционирования управляемых динамических систем описываются обыкновенными дифференциальными уравнениями. Этот класс систем характеризуется тем, что содержит модели, адекватно отражающие функционирование современных изделий машиностроения, технологических систем и т.д. Модели функционирования подразделяются:

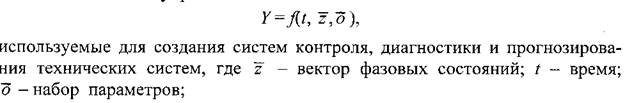на модели без управления– к неуправляемым.

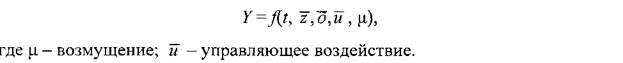модели с управлением, применяемые для создания систем автоматического управления:

Для описания процессов, протекающих в технологических агрегатах, используют математические выражения, которые составляют математическую модель процесса или объекта управления. В зависимости от того, какие математические формулы используют для описания процессов, математические модели подразделяют на линейные и нелинейные.

Линейной называется такая математическая модель описания объекта или процесса, для построения которой используют линейные дифференциальные или другие уравнения, т.е. уравнения, в которых связь между входными и выходными параметрами является линейной.

Нелинейной называется такая математическая модель описания объекта или процесса, для построения которой используют нелинейные уравнения, т.е. уравнения, в которых связь между входными и выходными параметрами является нелинейной.

С помощью линейной модели можно описать, например, реакции, протекающие в объеме ванны металлургического агрегата, теплоперенос в стенках печного агрегата и т.д.:

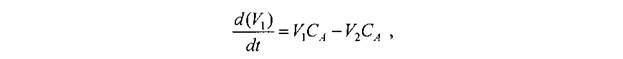
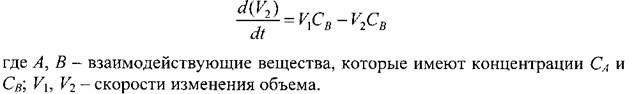
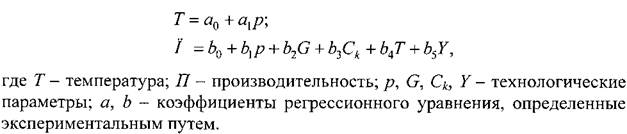Линейные модели могут использоваться для описания взаимосвязи входных и выходных параметров с помощью парных и множественных вероятностных (регрессионных) уравнений следующего вида:

При описании нелинейных моделей могут использоваться степенные зависимости xⁿ, показательные e^x, логарифмические, гиперболические, тригонометрические, интегральные, обратные тригонометрические и т.д.

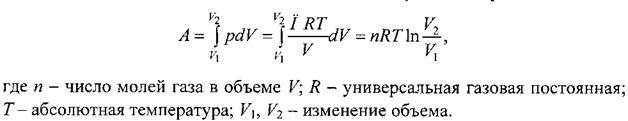Например, работу газа можно описать следующим выражением:

С помощью нелинейных моделей можно описать сложные физико-химические процессы, протекающие в металлургических агрегатах (печь обжига, восстановительно-окислительные процессы), и процессы массопереноса и физических превращений.

Многие взаимосвязи между входными и выходными параметрами могут быть описаны с помощью вероятностных нелинейных уравнений, напри-

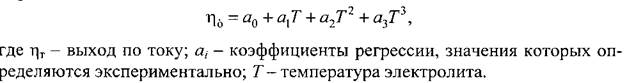мер, вида