Вращательного движения твёрдого тела
Моментом силы 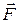 относительно неподвижной точки O называется векторная физическая величина, определяемая векторным произведением радиус-вектора
относительно неподвижной точки O называется векторная физическая величина, определяемая векторным произведением радиус-вектора 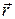 , проведённого из точки O в точку A приложения силы, на силу
, проведённого из точки O в точку A приложения силы, на силу 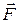 (рис.1.4.1):
(рис.1.4.1):
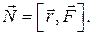 (1.4.1)
(1.4.1)
Здесь 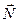 – псевдовектор, его направление совпадает с направлением движения правого винта при его вращении от
– псевдовектор, его направление совпадает с направлением движения правого винта при его вращении от 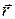 к
к 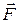 .
.
Модуль момента силы
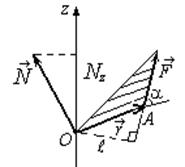 Рис. 1.4.1 Рис. 1.4.1 |
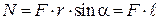 ,
,
где 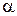 – угол между
– угол между 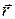 и
и 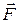 ,
, 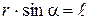 – кратчайшее расстояние между линией действия силы и точкой О – плечо силы.
– кратчайшее расстояние между линией действия силы и точкой О – плечо силы.
Моментом силы относительно неподвижной оси z называется скалярная величина 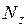 , равная проекции на эту ось вектора
, равная проекции на эту ось вектора 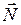 момента силы, определённого относительно произвольной точки O данной оси z (рис. 1.4.1).
момента силы, определённого относительно произвольной точки O данной оси z (рис. 1.4.1).
Работа при вращении тела равна произведению момента действующей силы на угол поворота:
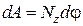 .
.
С другой стороны эта работа идёт на увеличение его кинетической энергии:
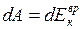 , но
, но
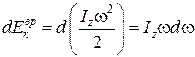 , поэтому
, поэтому
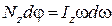 , или
, или 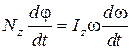 .
.
Учитывая, что 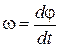 , получим
, получим
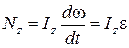 . (1.4.2)
. (1.4.2)
Получили основное уравнение динамики вращательного движения твёрдого тела относительно неподвижной оси: момент внешних сил, действующих на тело, равен произведению момента инерции тела на угловое ускорение.
Можно показать, что если ось вращения совпадает с главной осью инерции, проходящей через центр масс, то имеет место векторное равенство:

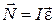 ,
,
где I – главный момент инерции тела (момент инерции относительно главной оси).
1.5 МОМЕНТ ИМПУЛЬСА И ЗАКОН ЕГО СОХРАНЕНИЯ
Моментом импульса материальной точки А относительно неподвижной точки О называется векторная физическая величина, определяемая векторным произведением:
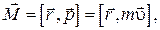 (1.5.1)
(1.5.1)
где 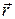 – радиус-вектор, проведённый из точки О в точку А;
– радиус-вектор, проведённый из точки О в точку А; 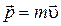 – импульс материальной точки (рис. 1.5.1).
– импульс материальной точки (рис. 1.5.1). 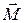 – псевдовектор, его направление совпадает с направлением поступательного движения правого винта при его вращении от
– псевдовектор, его направление совпадает с направлением поступательного движения правого винта при его вращении от 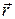 к
к 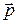 .
.
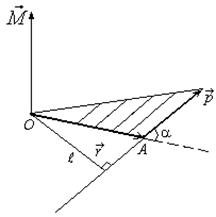 Рис. 1.5.1 Рис. 1.5.1 |
Модуль вектора момента импульса
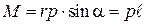 ,
,
где 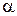 – угол между векторами
– угол между векторами 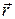 и
и 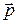 ,
, 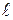 – плечо вектора
– плечо вектора 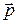 относительно точки О.
относительно точки О.
Моментом импульса относительно неподвижной оси z называется скалярная величина 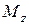 , равная проекции на эту ось вектора момента импульса, определённого относительно произвольной точки О данной оси.Значение момента импульса
, равная проекции на эту ось вектора момента импульса, определённого относительно произвольной точки О данной оси.Значение момента импульса 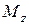 не зависит от положения точки О на оси z.
не зависит от положения точки О на оси z.
При вращении абсолютно твёрдого тела вокруг неподвижной оси z каждая отдельная точка тела движется по окружности постоянного радиуса 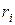 с некоторой скоростью
с некоторой скоростью 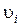 . Скорость
. Скорость 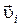 и импульс
и импульс 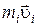 перпендикулярны этому радиусу, т.е. радиус является плечом вектора
перпендикулярны этому радиусу, т.е. радиус является плечом вектора 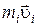 . Поэтому можно записать, что момент импульса отдельной частицы
. Поэтому можно записать, что момент импульса отдельной частицы
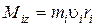
и направлен по оси в сторону, определяемую правилом правого винта.
Момент импульса твёрдого тела относительно оси есть сумма моментов импульсов отдельных частиц:
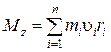 .
.
Используя формулу 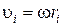 , получим
, получим
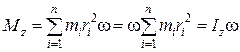 , т.е.
, т.е. 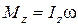 . (1.5.2)
. (1.5.2)
Таким образом, момент импульса твёрдого тела относительно оси равен произведению момента инерции тела относительно той же оси на угловую скорость.
Продифференцируем уравнение (1.5.2) по времени:
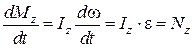 , т.е.
, т.е. 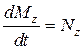 . (1.5.3)
. (1.5.3)
Это выражение – ещё одна форма основного уравнения (закона) динамики вращательного движения твёрдого тела относительно неподвижной оси: производная по времени от момента импульса механической системы (твёрдого тела) относительно оси равна главному моменту всех внешних сил, действующих на эту систему, относительно той же оси.
Можно показать, что имеет место векторное равенство 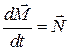 .
.
В замкнутой системе момент внешних сил 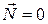 и
и 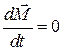 , откуда
, откуда
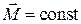 . (1.5.4)
. (1.5.4)
Выражение (1.5.4) представляет собой закон сохранения момента импульса: момент импульса замкнутой системы сохраняется.
Сопоставим основные величины и уравнения, определяющие вращение тела вокруг неподвижной оси и его поступательное движение (таблица 1.5.1).
Таблица 1.5.1
| Поступательное движение | Вращательное движение | Функциональная зависимость | ||||
| Линейное перемещение | S | Угловое перемещение | 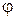 | 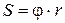 | ||
| Линейная скорость | 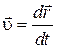 | Угловая скорость | 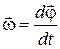 | 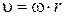 | ||
| Линейное ускорение | 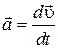 | Угловое ускорение | 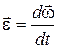 | 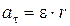 | ||
| Масса | m | Момент инерции | I | 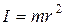 (для материальной точки) (для материальной точки) | ||
| Сила | 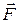 | Момент силы | 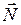 | 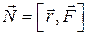 | ||
| Импульс | 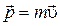 | Момент импульса 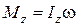 | 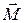 | 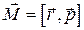 | ||
| Основное уравнение динамики | ||||||
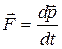 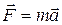 | 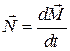 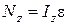 | |||||
Работа 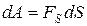 | Работа вращения 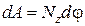 | |||||
Кинетическая энергия 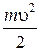 | Кинетическая энергия вращения 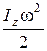 | |||||
Закон сохранения импульса 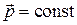 | Закон сохранения момента импульса 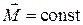 | |||||
2. ВЫПОЛНЕНИЕ РАБОТЫ
2.1. ОПИСАНИЕ ЛАБОРАТОРНОЙ УСТАНОВКИ
Лабораторная установка представлена на рисунке 2.1. На стойке 1 укреплена ось 2 подвеса сложного тела. Тело 3 подвешено на проволоке 4 и включает в себя массивную планку 5 с укрепленными на ней штифтами 6 для закрепления дополнительных грузов. Пары штифтов 6 расположены симметрично относительно точки крепления планки 5 к проволоке 4. Крепление планки 5 к проволоке 4 произведено в центре инерции планки 5. Добавочные грузы представляют собой сплошные цилиндры. Тело 3 приводится в колебательное движение нажатием рычага пускового механизма 7.
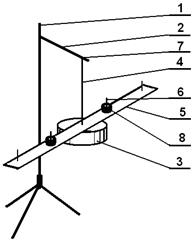 Рис. 2.1 Рис. 2.1 |
2.2 ЭКСПЕРИМЕНТАЛЬНОЕ ОПРЕДЕЛЕНИЕ МОМЕНТА
ИНЕРЦИИ ТЕЛА
В настоящей лабораторной работе в основу определения момента инерции тела положен метод крутильных колебаний. Исследуемое тело 3 (рисунок 2.1) отклоняют на небольшой угол 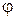 (
( 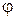 = 50 – 70). Под действием возникающей в результате отклонения тела от положения равновесия упругой силы проволоки и инертности тела последнее будет совершать гармонические крутильные колебания, описываемые уравнением:
= 50 – 70). Под действием возникающей в результате отклонения тела от положения равновесия упругой силы проволоки и инертности тела последнее будет совершать гармонические крутильные колебания, описываемые уравнением:
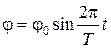 ,
,
где 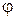 – угол отклонения тела от положения равновесия в момент времени
– угол отклонения тела от положения равновесия в момент времени 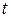 ;
; 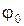 – максимальный угол отклонения (амплитуда).
– максимальный угол отклонения (амплитуда).
Период крутильных колебаний выражается формулой:
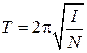 , (3.1)
, (3.1)
где 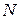 – направляющий момент - это постоянная величина, численно равная отношению крутящего момента силы к углу закручивания проволоки.
– направляющий момент - это постоянная величина, численно равная отношению крутящего момента силы к углу закручивания проволоки.
Период Т колебаний тела 3 можно определить экспериментально. Тогда из выражения (3.1) можно найти момент инерции тела 3:
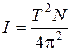 . (3.2)
. (3.2)
Укрепим на планке 5 грузы на штифты 6, ближайшие к центру инерции планки, по обе стороны от него. Расстояние от штифта до центра инерции планки 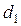 .
.
Момент инерции тела 3 вместе с грузами равен сумме моментов инерции его частей, поэтому
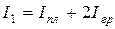 ,
,
где 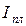 – момент инерции планки 5;
– момент инерции планки 5; 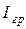 – момент инерции груза на штифте относительно оси, проходящей через центр инерции планки.
– момент инерции груза на штифте относительно оси, проходящей через центр инерции планки.
Согласно теореме Штейнера
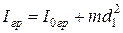 .
.
Грузы представляют собой сплошные цилиндры, их моменты инерции равны:
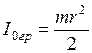 ,
,
где 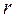 – радиус добавочного груза.
– радиус добавочного груза.
Тогда
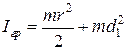 .
.
Окончательно имеем:
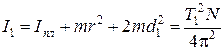 . (3.3)
. (3.3)
Переместим грузы на другую пару штифтов, удаленных от центра инерции планки на расстояние 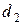 . Момент инерции сложного тела 3 в этом случае равен:
. Момент инерции сложного тела 3 в этом случае равен:
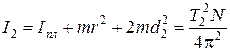 . (3.4)
. (3.4)
Вычтем из уравнения (3.3) уравнение (3.4), получим:
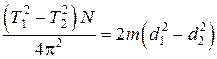 ,
,
отсюда
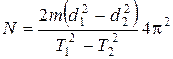 .
.
Тогда
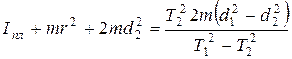
и
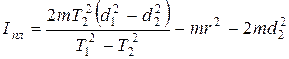 . (3.5)
. (3.5)
Приведя выражение (3.5) к общему знаменателю, получим:
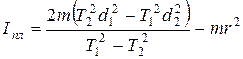 . (3.6)
. (3.6)
2.3 ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ
1. На штифты, ближайшие к проволоке, надеть добавочные цилиндрические грузы одинаковой массы 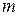 . Измерить расстояние
. Измерить расстояние 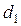 .
.
Нажатием рычага пускового механизма 7 (см. рисунок 2.1) привести исследуемое тело 3 в колебательное движение. Угол отклонения планки 5 от положения равновесия (по горизонтали) не должен превышать 50 – 70. При помощи секундомера измерить время 20 полных колебаний и вычислить период. Трижды повторить опыт.
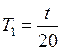 .
.
2. Переместить цилиндры на другую пару штифтов. Измерить расстояние 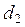 . Определить период колебаний Т2. Опыт повторить трижды.
. Определить период колебаний Т2. Опыт повторить трижды.
3. В каждой серии опытов вычислить средние значения Т1, Т2, 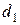 ,
, 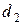 ,
, 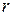 , т. Данные измерений и вычислений свести в таблицу 2.3.1. Определить погрешности измеренных величин и записать в таблицу 2.3.1.
, т. Данные измерений и вычислений свести в таблицу 2.3.1. Определить погрешности измеренных величин и записать в таблицу 2.3.1.
4. По формуле (3.6) рассчитать момент инерции исследуемого тела для средних значений входящих в формулу величин, вычислить абсолютную и относительную погрешности измерений.
5. Повторить п.п.1 – 4 для другого набора добавочных грузов, заполнить таблицу 2.3.2. измерений и вычислений, рассчитать момент инерции исследуемого тела.
6.По двум сериям опытов определить среднее значение момента инерции тела, вычис- лить абсолютную и относительную погрешности измерений.
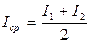 .
.
Таблица 2.3.1 измерений и вычислений для одного набора добавочных грузов
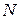 п/п п/п | 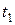 , с , с | 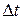 , с , с | Т1, с | 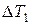 , с , с | 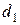 , м , м | 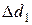 , м , м | 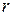 , м , м | 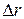 , м , м | 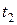 , с , с | 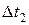 , с , с | Т2, с | 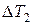 , с , с |
| ср |
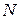 п/п п/п | 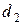 , м , м | 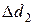 , м , м | т, кг | 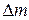 , кг , кг | 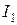 , кг×м2 , кг×м2 | 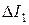 , кг×м2 , кг×м2 | 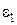 , % , % |
| – | – | – | |||||
| – | – | – | |||||
| – | – | – | |||||
| ср |
Таблица 2.3.2 измерений и вычислений для другого набора добавочных грузов
 п/п п/п | 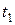 , с , с | 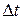 , с , с | Т1, с | 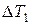 , с , с | 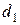 , м , м | 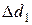 , м , м | 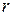 , м , м | 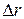 , м , м | 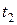 , с , с | 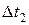 , с , с | Т2, с | 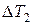 , с , с |
| ср |
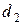 , м , м | 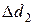 , м , м | т, кг | 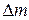 , кг , кг | 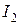 , кг×м2 , кг×м2 | 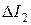 , кг×м2 , кг×м2 | 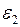 , % , % | |
| – | – | – | |||||
| – | – | – | |||||
| – | – | – | |||||
| ср |
2.4. ТРЕБОВАНИЯ К ОФОРМЛЕНИЮ ОТЧЕТА
Отчет должен содержать результаты измерений и вычислений, сведенные в таблицы 2.3.1. и 2.3.2.; примеры расчетов, а также вычисление абсолютных и относительных погрешностей.
2.5 КОНТРОЛЬНЫЕ ВОПРОСЫ
1. Перечислить и дать определение основных кинематических характеристик вращательного движения. Какова связь между линейными и угловыми величинами?
2. Что такое момент инерции? Какова роль момента инерции во вращательном движении?
3. Как определяется кинетическая энергия тела, вращающегося вокруг неподвижной оси? Привести вывод формулы.
4. Что называется моментом силы относительно неподвижной точки? Относительно неподвижной оси? Как определяется направление момента силы?
5. Выведите и сформулируйте основное уравнение динамики вращательного движения твердого тела.
6. Что такое момент импульса материальной точки? твердого тела? Как определяется направление момента импульса?
7. Сформулировать закон сохранения момента импульса.
8. Сопоставьте основные уравнения динамики поступательного и вращательного движения, прокомментировав их аналогию.
9. Вывести формулу экспериментального определения момента инерции твердого тела, которой Вы пользовались в данной работе.
2.6 ЛИТЕРАТУРА
1. Савельев, И.В. Курс общей физики [Текст]. В 3 т. Т.1. Механика. Молекулярная физика/И.В.Савельев. – СПб.: Лань, 2006. - 432с.
2. Иродов, И.Е. Механика. Основные законы [Текст]/ И.Е.Иродов. – М.: Лаборатория базовых знаний, 2002. – 312с.
