Частные случаи нормального закона распределения. 2 страница

ЗАДАЧА 5 (№ 1–10)

На трех станках при одинаковых и независимых условиях изготовлено 1000 деталей одного наименования. На первом станке изготовлено n₁ штук деталей, на втором станке – n₂ штук деталей и на третьем оставшиеся, т.е. 1000 – n₁–n₂. Вероятность каждой детали быть бездефектной равна 94%, если она изготовлена на первом станке, 95% – если на втором станке и 9 6% – если деталь изготовлена на третьем станке. Найдите вероятность того, что наугад взятая деталь окажется с дефектом.

(№ 11–20)

Квалификационную норму выполняла группа спортсменов из 1000 человек, среди которых было: n₁ – лыжников, n₂ – конькобежцев, остальные саночники, т.е. 1000 – n₁ – n₂. Вероятность выполнить квалификационную норму для лыжника равна 94%, для конькобежца – 95%, для саночника – 96%. Найдите вероятность того, что наудачу выбранный спортсмен не выполнит норму.

(№ 21–40)

На склад завезли 1000 шуб: из Греции – n₁ штук, из Аргентины – n₂ штук, из Германии остальные шубы, т.е. 1000 – n₁ – n₂. В партии шуб завезенных из Греции 6% бракованных шуб, из Аргентины – 5% бракованных шуб, из Германии – 4% бракованных шуб. Наудачу выбирается одна шуба из 1000 поступивших. Определите вероятность того, что выбранная шуба бракованная.

№

n1

n2

№

n1

n2

№

n1

n2

№

n1

n2

№

n1

n2

№

n1

n2

№

n1

n2

№

n1

n2

ЗАДАЧА 6 (№ 1–10)

В магазин поступила обувь от трех поставщиков. Первый поставщик доставляет m₁% пар обуви, второй – m₂% пар обуви и третий – m₃% пар обуви.

Среди обуви доставленной первым поставщиком – n₁% качественной, вторым – n₂% качественной обуви и третьим – n₃% качественной обуви. Куплена одна пара обуви и она оказалась бракованной. Определите наиболее вероятного поставщика этой бракованной пары обуви.

(№ 11–20)

В спартакиаде принимают участие спортсмены из трех регионов: Урала, Сибири и Дальнего Востока. Из Сибири участвуют – m₁%, с Дальнего Востока – m₂%, с Урала – m₃% всех участников. Среди спортсменов Сибири n₁% мастеров спорта, Дальнего Востока – n₂% мастеров спорта и Урала – n₃% мастеров спорта. Выбирают одного спортсмена из всех участников спартакиады, и он оказался не мастер спорта. Определите, наиболее вероятнее к какому региону он принадлежит.

(№ 21–40)

В группе туристов оказались люди, изучавшие английский, немецкий и французский языки. Из них: английский изучали – m₁%, немецкий – m₂%, французский – m₃%.

Среди туристов изучающих английский в совершенстве владеет языком – n₁%, изучающих немецкий – n₂%, изучающих французский язык – n₃%. Произвольным образом отобрали из группы одного туриста, который, как оказалось, только понимает язык, но не говорит на нем. Определите, наиболее вероятнее к какой подгруппе туристов он относится.

№

m1

m2

m3

n1

n2

n3

№

m1

m2

m3

n1

n2

n3

ЗАДАЧА 7 (№ 1–10)

Пусть всхожесть семян ржи составляет а%. Какова вероятность того, что из n посеянных семян ржи взойдет не менее к семян?

(№ 11–20)

В среднем по а% договоров страховая компания выплачивает страховую сумму. Найти вероятность того, что из n договоров с наступлением страхового случая будет связано с выплатой страховой суммы не более к договоров.

(№ 21–40)

Пусть а% изделий данного предприятия – это продукция высшего сорта. Некто приобрел n изделий, изготовленных на этом предприятии. Какова вероятность того, что из n приобретенных изделий не более к изделий высшего сорта?

№	а	n	к		№	а	n	к

ЗАДАЧА 8 (№ 1–10)

Известно, что в среднем а% всего числа изготовляемых заводом телефонных аппаратов является продукцией первого сорта. Чему равна вероятность того, что в партии из n штук аппаратов окажется от к₁ до к₂ штук аппаратов первого сорта? Найдите вероятнейшее число телефонных аппаратов первого сорта к₀ в данной партии и вычислите соответствующую вероятность Р(к₀).

(№ 11–20)

Вероятность вызревания кукурузного стебля с тремя початками равна а%. Чему равна вероятность того, что среди n стеблей кукурузы число вызревших будет от к₁ до к₂ штук? Найдите наивероятнейшее число вызревших стеблей к₀ и вычислите соответствующую вероятность Р(к₀).

(№ 21–40)

При обследовании уставных фондов банков установлено, что а% банков имеют уставной фонд свыше ста миллионов рублей. Найти вероятность того, что среди обследуемых n банков имеют уставной фонд свыше ста миллионов рублей от к₁ до к₂ банков. Найдите наивероятнейшее число к₀ банков, имеющих уставной фонд свыше ста миллионов рублей, и вычислите соответствующую вероятность Р(к₀).

№	а	n	к1	к2		№	а	n	к1	к2

ЗАДАЧА 9 (№ 1–10)

Вероятность того, что пассажир опоздает к отправлению поезда равна р. Найти вероятность того, что из n пассажиров опоздает к отправлению поезда: 1) к пассажиров; 2) не более к пассажиров.

(№ 11–20)

Прядильщица обслуживает n веретен. Вероятность обрыва нити на одном веретене в течение одной минуты равна р. Найдите вероятность того, что в течение одной минуты обрыв произойдет: 1) на к веретенах; 2) не белее, чем на к веретенах.

(№ 21–40)

Вероятность того, что зерно пшеницы не прорастет равна р. Какова вероятность того, что n из посеянных семян не дадут всходов: 1) ровно к семян; 2) не более к семян.

№	р	n	к		№	р	n	к
	0,001					0,02
	0,002					0,02
	0,003					0,02
	0,004					0,02
	0,005					0,02
	0,006					0,02
	0,007					0,008
	0,008					0,006
	0,009					0,004
	0,01					0,002

№	р	n	к		№	р	n	к
	0,01					0,001
	0,01					0,009
	0,01					0,008
	0,01					0,007
	0,01					0,006
	0,01					0,005
	0,01					0,004
	0,01					0,003
	0,02					0,002
	0,02					0,001

Решение типовых задач по теме «Случайные события»

Задача 1.Среди 15 студентов группы, из которых 8 девушек, разыгрывается 6 билетов. Какова вероятность того, что среди обладателей билетов окажутся 4 девушки?

Решение. Испытание – разыгрывается 6 билетов среди группы студентов.

Событие 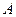– среди обладателей 6 билетов будут 4 девушки и 2 юноши.

Найти 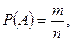где m число благоприятствующих событию 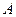исходов данного испытания и n – число всех исходов данного испытания.

Число всех способов распределения 6 билетов среди 15 студентов равно числу сочетаний из 15 элементов по 6, т.е.

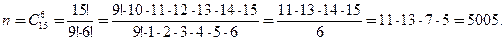
Число способов отбора четырех девушек из 8 равно 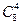. Каждая такая четверка может сочетаться с каждой парой из 7юношей: число таких пар равно 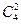. Значит,

.

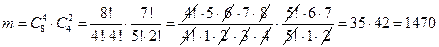Тогда искомая вероятность составляет: .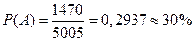

Ответ. Вероятность того, что среди обладателей билетов будет четыре девушки равна 0,2937.

Задача 2.Из ящика, содержащего 20 небракованных и 10 бракованных изделий, поочередно извлекается два изделия без возвращения. Какова вероятность при первом и втором извлечениях получить небракованные изделия?

Эту же задачу можно решить двумя способами.

Решение 1. Испытание – из ящика поочередно извлекаются 2 изделия.

Событие 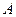– извлекли два небракованных изделия. Переномеруем изделия, тогда отдельным исходом будет появление пары изделий из ящика, имеющих определенные номера.

Используем классическое определение вероятности:

.

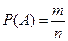Теперь подсчитаем общее число m благоприятных событию 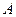элементарных исходов, т.е. появление двух небракованных изделий. Всего небракованных изделий 20 , значит

.

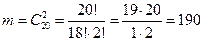n – различные элементарные исходы, т.е. такие пары изделий, которые отличаются друг от друга хотя бы номером одного изделия. Тогда число всех исходов

.

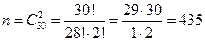Тогда

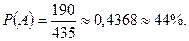
Решение 2. Для решения применим теорему умножения для зависимых событий. Событие А – взяли небракованое изделие при первом извлечении, событие В – взяли небракованое изделие при втором извлечении, событие С – взяли два небракованых изделия. Тогда сложное событие С, вероятность которого надо найти, выражается через А и В по формуле

.

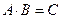Событие В зависит от события А, т.к. извлеченное изделие в ящик не возвращается. По теореме умножения вероятностей для зависимых событий будем иметь

.

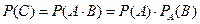Но 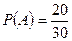и 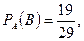т.к. одно извлеченное изделие небракованное в ящик не возвращается. Следовательно,

.

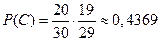Ответ. Вероятность извлечения из ящика двух небракованных изделий равна 0,4368 , т.е. примерно 44%.

Задача 3.Стрелок стреляет по мишени, разделенной на 3 области. Вероятность попадания в первую область равна 0,45; во вторую – 0,35. Найти вероятность того, что стрелок при одном выстреле попадет либо в первую, либо в третью область.

Решение. Испытание – стрелок стреляет по мишени. Событие А – стрелок попал в первую область, событие В – стрелок попал в третью область, событие С – стрелок попал во вторую область; (А+В+С) – достоверное событие, так как А;В;С образуют полную группу событий

.

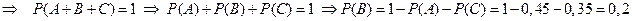События А и В – несовместные, то есть попадание в одну область исключает попадание в другую область. Искомая вероятность

.

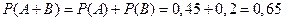Ответ. Вероятность попадания стрелка в цель при одном выстреле или в первую, или в третью область равна 0,65, или 65%.

Задача 4.В урне 30 шаров: 10 красных, 5 синих, 15 белых. Найти вероятность того, что вынутый наудачу шар будет цветной (не белый).

Задачу можно решить двумя способами.

Решение 1. Испытание – из урны вынимают один шар. Событие А – вынутый шар цветной, т.е. либо красный, либо синий. Событие В – вынутый шар красный. Событие С – вынутый шар синий. События В и С несовместны.

.

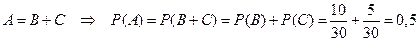Решение 2. Используем классическое определение вероятности: 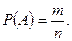Найдем 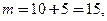число исходов, благоприятствующих событию А, и 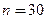– общее число исходов данного испытания. Искомая вероятность равна

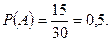
Ответ. Вероятность вынуть цветной шар из коробки равна 0,5, или 50%.