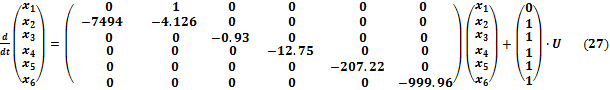Определение жордановой канонической формы уравнений состояния

Суть жордановой канонической формы состоит в разложении исходной системы на независимые параллельные подсистемы. При этом сумма порядков подсистем равняется общему порядку системы, а такое представление в целом удобно для анализа динамики системы и исследования ее свойств.

Для получения жордановой канонической формы передаточную функцию исследуемой системы представляют в виде суммы простейших дробей, каждую из которых реализуют с помощью отдельной схемы.

Разложение передаточной функции на сумму простых дробей можно производить в системе MatLab или MathCad.

Система MatLab.

Для разложения заданной передаточной функции на сумму простых дробей испоьзуем следующую команду системы MatLab: [r,p,k]=residue(a,b)

» a=[28.8 1440];

» b=[0.000000078 0.00009555 0.01843 1.008 131.9 1667 1440];

» [r,p,k] = residue(a,b)

r = коэффициенты

0.0004

-0.0368

-0.0797 + 0.0968i

-0.0797 - 0.0968i

-0.7968

0.9926

p = полюса

-999.96

-207.22

-2.06 + 86.54i

-2.06 - 86.54i

-12.75

-0.93

k = [ ] коэффициенты целой части.

Таким образом, результат разложения передаточной функции на сумму простых дробей в системе MatLab следующий:

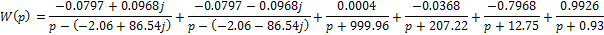
Система MathCad.

Рис. 5. Разложение передаточной функции на сумму простых дробей в системе MathCad.

Разложение передаточной функции на сумму простых дробей в системе MatLab показало наличие пары комплексно сопряженных корней:

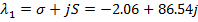
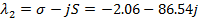
Соответствующие им две простейшие дроби первого порядка в разложении объединяются в одну дробь второго порядка с вещественными коэффициентами.

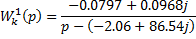
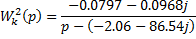
Используя систему MatLab, найдем сумму двух дробей первого порядка:

» W1= tf ( [-0.0797+0.0968i] , [1 2.06-86.54i] );

»W2 = tf ( [-0.0797-0.0968i] , [1 2.06+86.54i] );

» W12=W1+W2

Transfer function:

– 0.1594 s – 17.08

s^2 + 4.123 s + 7493

Таким образом,

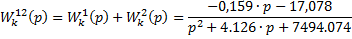
Следовательно, передаточную функцию исследуемой САУ можно записать в следующем виде:

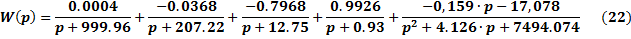
Полученный ответ совпадает с ответом, который получен в системе MathCad, следовательно, разложение передаточной функции на сумму простых дробей выполнено правильно.

Граф жордановой канонической формы уравнений состояния при наличии двух комплексных сопряженных корня представлен на рис. 6.

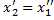
Рис. 6. Граф системы для жордановой канонической формы.

В матричной записи комплексная клетка Жордана будет выражаться Фробениусовой формой. В этом случае:

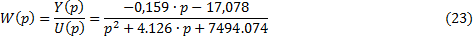
Запишем дифференциальное уравнение, соответствующее данной передаточной функции:

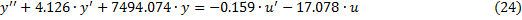
Дифференциальное уравнение содержит в правой части не только управляющее воздействии, но и его производную. В этом случае производятся следующие замены:

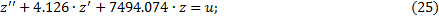
Пусть

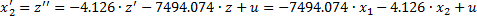
Из уравнения (26) следует:

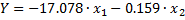
Таким образом, соответствующая клетка Жордана в матрице состояний системы будет иметь следующий вид:

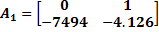
Уравнение в пространстве состояний, соответствующее графу системы для жордановой канонической формы легко получить из графа системы.

Матричная запись этих уравнений имеет следующий вид: