Лестіру функциясының қасиеттері.

1) Үлестіру функциясының мәні мына кесіндіде жатады [0;1]:

2) F(x) – кемімейтін функция, яғни F(x₂) 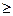F(х₁), егер x₂>x₁.

Салдар 1. Х кездейсоқ шамасының қабылдайтын мәні (a;b) интервалының ішінде жату ықтималдығы осы интервалдағы үлестіру функциясының өсімшесіне тең:

=F(b)-F(a)

Салдар 2: Х үздіксіз кездейсоқ шамасының тек қана бір мән қабылдайтының ықтималдығы 0-ге тең.

3) Егер Х үздіксіз кездейсоқ шамасының мүмкін мәндері (a;b) интервалында жататын болса, онда 1) F(x)=0 егер x a;

2) F(x)=1 егер x>b.

Салдар 3. Егер Х үздіксіз кездейсоқ шамасының мүмкін мәндері барлық х осінде жататын болса, онда келесі шектер тура:

F(x)=0,

F(x)=1

Мысал.

Х үздіксіз кездейсоқ шамасының үлестіру заңы берілді:

х
р	0,06	0,056	0,053	0,050	0,781

Есептің шарты бойынша Х үзіліссіз кездейсоқ шамасының үлестіру функциясының графигін салыңыз:

Шешуі:

Х кездейсоқ шамасы 1-ден кем мән қабылдамайды. Осыдан, , онда оқиға Х<х – мүмкін емес, ал оның ықтималдығы нөлге тең. Сондықтан Х кездейсоқ шамасының кез келген мәнінде үлестіру функциясының мәні нөлге тең.

Кез келген қос теңсіздікті қанағаттандыратын х үшін 1<x 2, F(x) функциясының қабылдайтын мәні 0,06 - ға тең. Егер мысалы, x=1,2, онда F(x) оқиғасының ықтималдығы x<1,2.

Х кездейсоқ шамасы 1,2 кем мән бір ғана жағдайда қабылдайды: 1-ге тең мән 0,06 дәлдікпен алынады.

Кез келген қос теңсіздікті қанағаттандыратын х үшін 2<x 3, F(x)=0,06+0,056=0,116.

Мысалы.

х=3. Онда F(3) х<3 оқиғасының ықтималдығын өрнектейді.

Ол екі жағдайда болуы мүмкін: Х-тің мәні 1-ге тең (ықтималдығы 0,06), немесе мәні 2-ге тең (ықтималдығы 0,056)

Ықтималдықтарды қосу теоремасын пайдаланып, көрсетілген F(x) функциясының мәнін х=3 болғанда табамыз:

F(x) =

Үлестіру функциясының графигі:

Ықтималдықтың тығыздық функциясы, қасиеттері.

Егер Х кездейсоқ шамасының үлестіру функциясы F(X) – тан алынған бірінші туындыны үлестіру тығыздығы деп атайды:

f(x)=F X).

Бұл анықтамадан үлестіру функциясы үлестіру тығыздығына алғашқы функция болады.

F(x)=

Үлестіру тығыздығы f(x) –ті дифференциалдық функция деп атайды.

Здіксіз кездейсоқ шаманың берілген интервалға түсетінінің ықтималдығы туралы теорема.

Х кездейсоқ үздіксіз шамасы (a,b) интервалында жататын мәндер қабылдайтындығының ықтималдығы шектері а дан b – ға дейінгі үлестіру тығыздығынан алынған анықталған интегралға тең.

P(a<X<b)= .

Геометриялық дегеніміз: Х кездейсоқ үздіксіз шамасы (a,b) интервалында жататын мәндер қабылдайтындығының ықтималдығы Ох осімен және f(x) үлестіру қисығымен және x=a, x=b түзулерімен шектелген қисық сызықты трапецияның ауданына тең.

Үлестіру тығыздығының қасиеттері:

1) Үлестіру тығыздығы –теріс емес функция:

f(x) 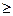0

2) Шектері (- ) (+ ) тең үлестіру тығыздығынан алынған меншіксіз интеграл бірге тең:

=1

«Үлкен сандар заңы. Бернулли теоремасы».

Чебышев теңсіздігі

Бұрын байқалған, кейбір белгілердің сандық сипаттамаларының орта арифметикалық мәні (өлшемдердің қорытындысы ж.т.б.) осындай біртекті құбылыстардың үлкен саны көп емес тербелістерге ұшыраған. Орта мәнін айтқанда құбылыстарға тән заңдылық бар, онда әр түрлі факторлар әсері өзара жойылады, олардағы бақылаулардың қорытындысы кездейсоқ болып қалады. Теориялық тілде бұл орта мәннің тәртібін тек үлкен сандар заңы арқылы түсіндіруге болады, кездейсоқ құбылыстар арқылы жалпы шарттар орындалатын болса, онда арифметикалық ортаның орнықтылығы ақиқат оқиға. Осы шарттар үлкен сандар заңының маңызды мазмұнын құрайды.

Үлкен сандар заңы сөйлемдердің жиынтығы, орта арифметикалық мәннің кездейсоқ шамалардың жеткілікті көптеген сандарының тұрақты шамадан ауытқуы - олардың математикалық күтімдерінің орта арифметикалық мәндерінің қандай да бір берілген кішкентай 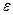>0 артпайды.

,

мұндағы - Х кездейсоқ шамалардың математикалық күтімі.

Чебышев теоремасы түрінде берілген үлкен сандар заңын қарастырайық.

Чебышев теоремасы

Егер Х₁,Х₂…Х_n кездейсоқ шамалардың дисперсиясы бір С тұрақты шамасымен шектеулі болса, ал олардың саны жеткілікті үлкен болса, онда берілген 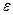>0 саны қандай кіші болса да, осы кездейсоқ шамалардың олардың математикалық күтімінен ауытқуы абсолюттік шамасы бойынша қандай да бір 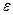санынан артпайды, бірге жақын болады.

Чебышев теоремасы негізінде статистикадағы таңдамалы әдіс құрылған, шағын кездейсоқ таңдаманы салыстырғанда зерттелетін объектердің түгел жиынтығы алынады. Кішкентай мақтаның уысын алғанда түгел мақтаның сапасы туралы айтылады. Дәннің сапасын, оның кішкентай дәндерінен байқап көруге болады.

n тәуелсіз тәжірибелердің әрқайсысында А оқиғасының көріну ықтималдығы Р-ға тең. Оқиғаның көрінуінің салыстырмалы жиілігі қандай болатынын алдын ала айтуға болмайды. Якоб Бернуллидің (1713ж) дәлелдеген «үлкен сандар заңы» атты және ықтималдықтар теориясының ғылым ретінде басталуына мүмкіндік берген теоремасы осы сұраққа жауап бере алады.

Бернулли теоремасы.

Егер n тәуелсіз тәжірибелерде А оқиғасының көріну ықтималдығы Р тұрақты болғанда, онда бірге жақын салыстырмалы жиілігінің Р ықтималдығынан ауытқуының ықтималдығы абсолюттік шамасы бойынша аз болады, егер тәжірибелер саны жеткілікті үлкен болса.

Дәріс №6.

Тақырыбы: «Математикалық статистика пәні. Таңдамалы әдіс».