Лекция 8. Силовой анализ механизма

Определение: Приведённым моментом инерции называется момент инерции такой фиктивной массы на начальном звене, при наличии которого кинетическая энергия начального звена равна кинетической энергии всего механизма.

I_пр – величина переменная.

Примерный вид графика зависимости .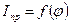

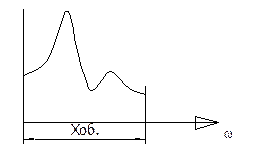
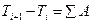
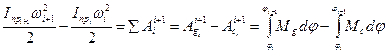
Приведённый момент сил.

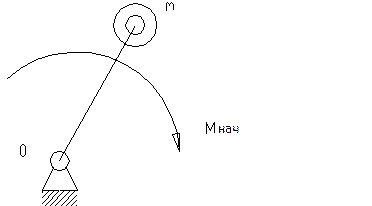
Указанные работы удобно вычислять, используя понятие о приведённом к кривошипу машины моменте сил, соответственно сил движущих (со стороны двигателя) и сил сопротивления (со стороны машин).

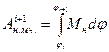
Произвольное звено:

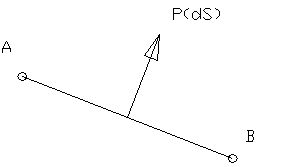
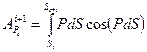
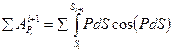
Введём скорости в точки приложения сил:

;

;

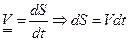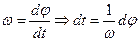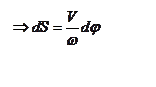
далее, в уравнении 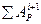подставим dS:

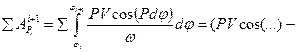это есть мощность 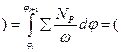но по следствию из теоремы о рычаге Жуковского ,

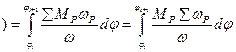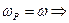
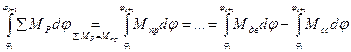
Определение: Приведённым моментом сил называется момент такой фиктивной силы, на начальном звене, работа и мощность, которого равна работе и мощности всех сил механизма.

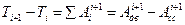
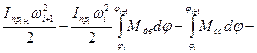уравнение кинетической энергии

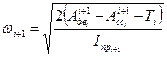для случая созданной динамической модели механизма, т.е. есть только Н.М., но на нём сосредоточена вся фактическая масса и сила.

Режимы работы механизма.

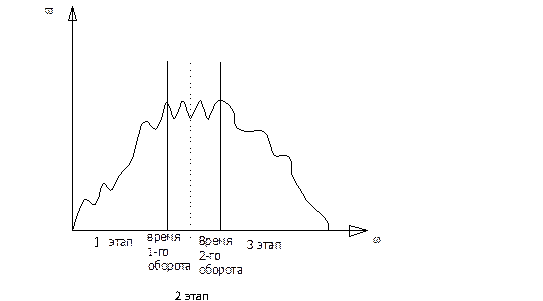
I этап – разгон машины: А_дв > А_сс

II этап – установившийся режим работы машины: А_дв = А_сс

Есть две характеристики второго этапа:

1. Такой, как приведён выше;

2. Постоянное изменение ω, т.е. по заданному закону.

III этап – остановка (торможение) машины: А_дв < А_сс.

Коэффициент неравномерности хода.

Приведение сил основано на равенстве секундных работ (мощностей) реальных сил и моментов приложенных к звеньям механизма, на их возможных перемещениях и суммарного приведённого момента, приложенного к начальному звену на его возможное перемещение.

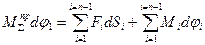если ,

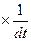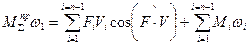
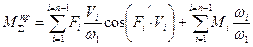
Задан закон изменения ω:

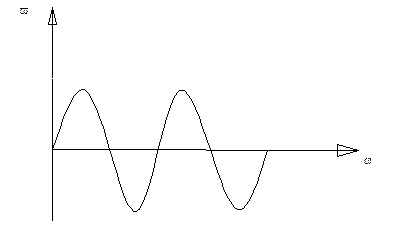
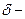коэффициент неравномерности хода машины.

;

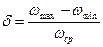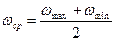
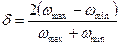
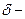для станков = 0.05 – 0.08

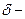для прессов = 0.15 – 0.20

Динамическое исследование механизмов для случаев, когда силы зависят от скорости.

1. Строятся 12 положений механизма.

2. Строятся 12 рычагов Жуковского.

3. Пользуясь Р.Ж., как планами скоростей, определяется I_пр и стоится график:

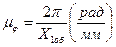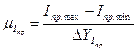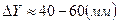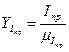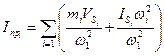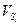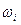, ; , . где , и 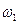берутся с рычага Жуковского с учётом масштаба. Учитывая, что приведённый момент инерции механизма должен быть увеличен путём установки на кривошип маховика с моментом инерции 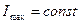график 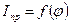по оси ординат, соответственно, увеличивается.

4. М_п.с., [М_п.с., φ] , , .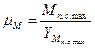

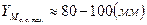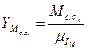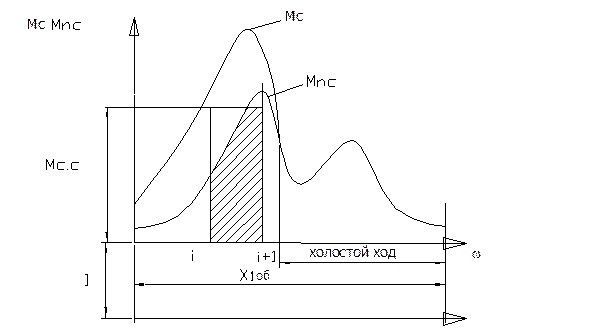
Величина приведённого момента сил полезного сопротивления ( с учётом силы полезного сопротивления и сил тяжести, без учёта сил трения) равна алгебраической сумме моментов сил относительно полюса P_P рычага Жуковского, при плече сил (мм) относительно полюса тщательно изменяются на точно построенных рычагах Жуковского. При этом знак (+) в уравнении моментов присваивается моменту направленному против 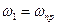, а знак (–) – моменту, направление которого совпадает с направлением СО. Отложив соответствующие отрезки на ординарных прямых соответствующих 12(8) положениям механизма, проводим кривую зависимости .

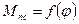5. Определить работу:

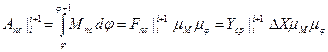
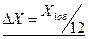
Вычислив работу сил сопротивления по интервалам найдём работу сил за один оборот: 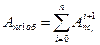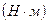. Далее необходимо произвести учёт работы силы трения. Работу силы трения распределяют на две части:

- постоянную на протяжении всего хода рабочего звена;

- переменную в каждом положении во время рабочего хода;

при этом, отношение 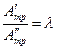. В результате получаем из двух уравнений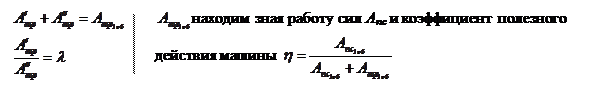

; .

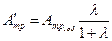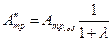Для учёта 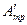на графике 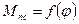опустим ось φ на величину ? и получим новую ось абсцисс с началом в точке О.

; .

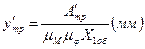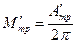Для распределения переменной части работы сил трения 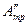находится сумма работ сил полезного сопротивления за время рабочего хода 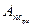, сложив 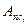для всех интервалов рабочего хода.

Тогда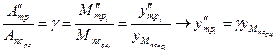

6. М_дв

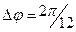обычно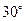

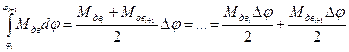
7. .

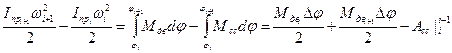8. Характеристика электродвигателя.

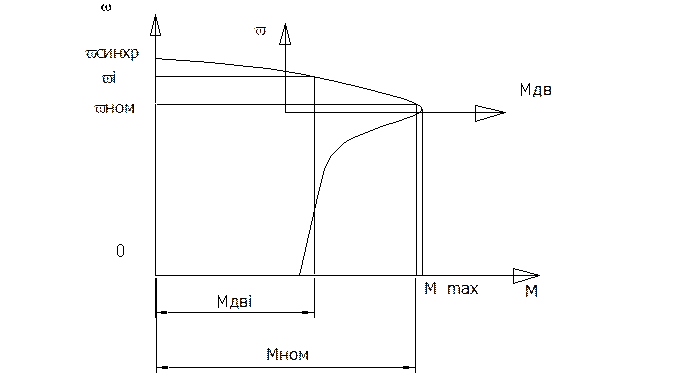
Общий вид характеристики асинхронного электродвигателя трёхфазного тока.

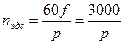(р = 1, 2, 3, 4 – число полюсов). Рабочая часть характеристики – кривая линия небольшой кривизны, поэтому в дальнейшем будем полагать рабочий участок прямолинейным.

На листе графики М_дв – ω², ω² – φ и М_дв – φ стоятся относительно друг друга следующие:

1. Совпадение осей О₂ω² и Оφ характеристик М_дв – ω² и М_дв – φ;

2. Совпадение осей О₁φ и О₂М_дв характеристик ω² – φ и М_дв – ω²;

3. Параллельность осей О₂ω² и О₁ω², что позволяет исключить ось ω² и от графика ω²φ прейти простым построением к графику М_g – φ на поле графика М_с – φ, построенного ранее.

4. Масштаб по осям ординат ОМ и О₂М_g должен быть одинаковым.

5. Построение характеристик двигателя М_дв – ω² производится в следующем порядке. Отложив отрезки 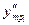от зависимости 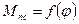найдём точки графика 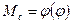, а соединив их кривой получим графическую зависимость 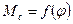, график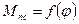и и 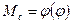сопрягаются в начале холостого хода.

6. О выборе электродвигателя.

Зная полную работу сил сопротивления сил трения 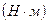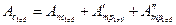можно определить мощность 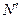электродвигателя (потребную): 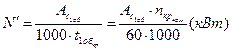, где 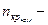частота вращения кривошипа (мин^-1), величина известная. Зная потребную мощность и синхронное число оборотов электродвигателя в линейке (1500, 1000, 750) находят необходимый электродвигатель, по условию 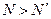, ближайший к 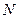. Выписываются характеристики электродвигателя (марка, мощность, синхронную и номинальную частоту вращения, а также значение допустимой перегрузки). Для решения задачи динамики необходимо знать синхронную n_c и номинальную n_н частоту вращения кривошипа. Номинальное число n_н (мин^-1) заданно проектанту. Выбрав электродвигатель известно n_эдн (мин^-1), следовательно можно определить инерционное число 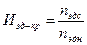. Теперь можно найти синхронную частоту вращения кривошипа .

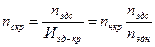Зная 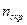, 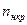вычисляем 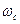и 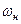по общей формуле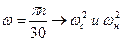

Можно, зная 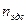и передаточное число .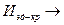

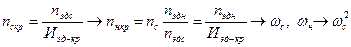Вычислив номинальную частоту вращения кривошипа находим величину номинального момента электродвигателя приведённого к кривошипу.

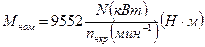
Лекция 9.

9.

;

; ; ;

;

;

; ;

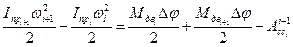
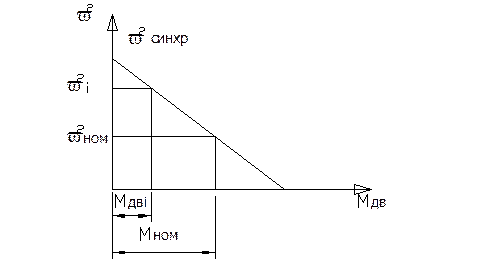
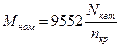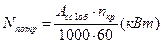
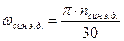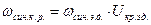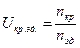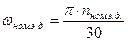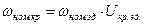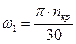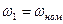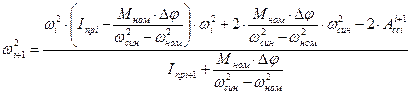
Маховик и его роль в машине.

Маховик – это аккумулятор энергии.

Маховик накапливает энергию на тех участках, где А_дв > А_сс.

Маховик отдаёт энергию, где А_дв < А_сс.

Расчёт энергии маховика:

; .

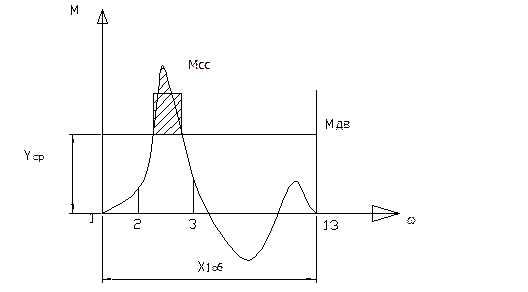
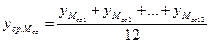
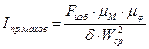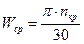Если маховик отсутствует, то график М_дв будет совпадать с М_сс. При бесконечном большом маховике график М_дв будет прямая. При обычных величинах график М_дв будет кривая.

Построение характеристики электродвигателя.

Определение момента инерции маховика.

Колебания величины угловой скорости кривошипа не должны превосходить некоторой величины 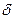. Для станков допускается от 0.02 до 0.05, для кузнечнопрессовых машин от 0.1 до 0.2 и т.д. Величина 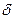вычисляется ; .

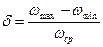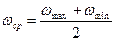Для обеспечения нужного значения 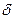необходимо выбрать и установить на валу кривошипа маховик с соответствующим значением момента инерции I_махов. Подбор маховика можно производить следующим образом. На оси ординат графика 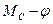в масштабе 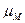откладываются 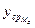(можно отложить М_н, найденное ранее) и проводится горизонтальная прямая. Выше этой прямой окажется часть графика 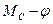. Необходимо найти величину площади между прямой M_н и кривой 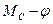. Это будет так называемая избыточная площадь F_изб (мм²). Затем необходимо воспользоваться формулой 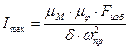, задавшись желательным коэффициентом 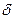. Выбрав маховик, необходимо учесть момент инерции маховика при определении 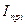как 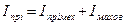, отразив это на графике 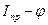, опустив ось абсцисс. Построив зависимость 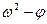можно проверить правильность выбора момента инерции маховика. Это производится путем сравнения 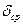и 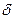заложенного в расчёт. При определени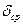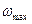и , и 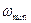берутся с графика зависимости .

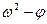Если 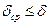, то момент инерции маховика достаточен;

Если 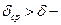момент инерции маховика следует увеличить.

Теория зубчатых зацеплений. Цилиндрические зубчатые колёса. Основные термины и определения.

Определения:

1. полюс – это мгновенный центр скоростей в относительном движении;

2. центройды – это воображаемые окружности, жестко связанные с колёсами, которые катятся друг по другу без скольжения;

3. начальная скорость – это центройда в зацеплении двух колёс.

Под центроидой понимается геометрическое место мгновенных центров скоростей в относительном движении профилей двух звеньев. Мгновенный центр скоростей в относительном движении двух профилей называется полюсом.

Передаточное отношение (U).

; ; ; ; ; ; ; .

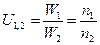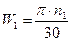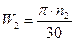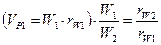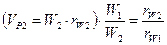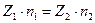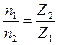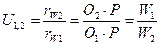Основной закон зацепления.

Нормаль к профилям в точке контакта должна проходить через полюс и делить межосевой перпендикуляр на отрезки обратнопропорциональные угловым скоростям.

Определение: линия зацепления – это путь, пройденный точкой контакта профилей.

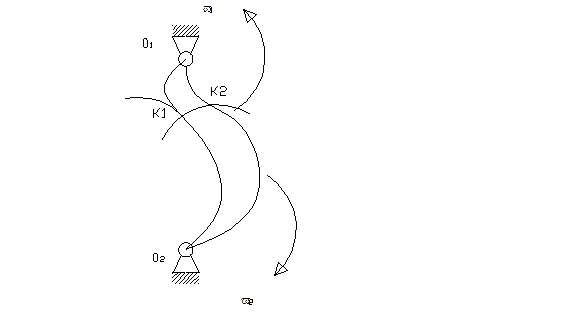
Определение: линия зацепления – это геометрическое место точек контакта профилей, отмеченных в неподвижной плоскости.

В современном машиностроении наиболее распространенным типом механической передачи является зубчатая. В этих передачах движение предаётся с помощью зацепления пары зубчатых колёс. Зубчатые передачи используют при мощностях, начиная от ничтожно малых до измеряемых десятками тысяч киловатт. Передаваемые моменты достигают 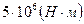. Диаметры колёс судовых установок в передачах на гребной винт достигают 6 метров. Округленные скорости колеблются от ничтожно малых до 150 м/с и обеспечивают передачу движения между произвольно расположенными в пространстве валами без проскальзывания, что обеспечивает постоянное передаточное отношение с наименьшие потери на трение.

Преимущества зубчатых передач по сравнению с другими:

а. высокая надёжность в работе;

б. компактность;

в. высокий КПД (0.96 – 0.97);

г. сравнительно малые нагрузки на валы и подшипники;

д. постоянство передаточного отношения;

е. простота обслуживания.

Недостатки:

а. высокие требования к точности изготовления и монтажа;

б. шум при больших скоростях;

в. большая жёсткость, не позволяющая компенсировать динамические нагрузки.

По взаимному расположению геометрических осей валов: цилиндрическое (косозубые, прямозубые, шевронные, с криволинейными зубьями), конические – при пересекающихся осях, гипоидные конические передачи при перекрещивающихся осях, винтовые – цилиндрические передачи перекрещивающихся осях.

Для преобразования вращательного движения в поступательное и наоборот применяется реечная передача, которая является частным случаем цилиндрической зубчатой передачи. Рейку рассматривают как часть колеса, диаметр которого обращается в бесконечность.

По форме бокового профиля зубья бывают: эвольвентные, циклоидальные и круговые (зацепление Новикова). В современном машиностроении и курсе ТММ широко рассматриваются эвольвентные З.П.

По сравнению с другими видами зацеплений, эвольвентное зацепление имеет некоторые преимущества:

1. использование стандартизованного инструмента с прямолинейными режущими кромками для изготовления эволвентных зубчатых колёс;

2. простота модификации поверхности зуба (преднамеренное отклонение поверхности зуба от теоретической для компенсации действия факторов, отрицательно влияющих на работу эвольвентной зубчатой передачи);

3. возможность изготовления зубчатых колёс с эвольвентным профилем при смещении инструмента для улучшения показателей качества зацепления или при заданном межосевом расстоянии передачи;

4. нечувствительность эвольвентной зубчатой передачи к колебания межосевого расстояния при монтаже (передаточное отношение З.П. не изменяется);

5. взаимозаменяемость эвольвентных З.К. одного модуля.

Свойства эвольвентного зацепления.

Свойства:

1. Линия зацепления – прямая.

2. .

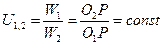3. 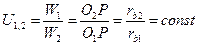. Передаточное отношение остаётся постоянны при изменении межцентрового расстояния.

4. Нарезается по методу обработки инструментом реечного типа.

Основы теории зацепления и передаточное отношение.

При работе зубчатых передач, зубья одного колеса входят в впадины другого, при этом боковая поверхность зуба ведущего колеса давит на боковую поверхность зуба ведомого колеса. Профили зубьев пары колёс должны быть сопряжёнными, т.е. заданному профилю зуба одного колеса должен соответствовать вполне определённый профиль зуба другого колеса. Чтобы обеспечить постоянство передаточного отношения, профили зубьев нужно очертить такими кривыми, которые удовлетворяли бы требованиям основной теоремы зацепления.

Теорема зацепления: общая нормаль, проведённая через точку касания двух профилей, делит межосевое расстояние на части, обратно пропорциональные угловым скоростям сопряжённых колёс.

Для доказательства теоремы рассмотрим пару сопряжённых зубьев в зацеплении. Профили зубьев шестерни и колеса соприкасаются в точке К, называемой точкой зацепления. Центры вращения О₁ и О₂ расположены на неизменном расстоянии друг от друга (межосевое расстояние – 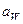). При вращении шестерня с угловой скоростью 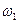давит на зуб колеса, сообщая последнему угловую скорость 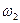. Проведём через точку К общую для обоих профилей касательную ТТ и нормаль NN. Окружные скорости точки К относительно центров вращения О₁ и О₂ 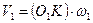и 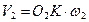. Разложим V₁ и V₂ на составляющие по направлению NN и по направлению ТТ: ; .

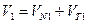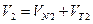Для обеспечения постоянного касания профилей необходимо соблюдение условия 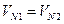, т.к. при 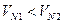зуб шестерни отстанет от зуба колеса, а при 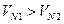произойдёт врезание зубьев. Опустим из центров О₁ и О₂ перпендикуляры О₁А = h₁ и O₂B = h₂ на нормаль NN. Углы, образованные между перпендикуляром h₁ и линией О₁К и перпендикуляром h₂ и линией О₂К обозначим соответственно α₁ и α₂. Так как вектор скорости V₁ перпендикулярен к линии О₁К, а вектор V_N1 перпендикулярен к линии О₁А = h₁, то угол между этими векторами будет равен α₁. Аналогично можно доказать, что угол между векторами V₂ и V_N2 , будет равен α₂.

Из построений получаем ,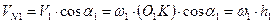

;

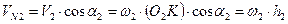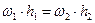или .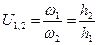

Из подобия треугольников О₁АР и O₂BР запишем, что 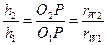или окончательно получим 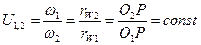, что и требовалось доказать.

Прямая О₁О₂ называется межосевой линией колёс. Общая нормаль NN профилем пересекает межосевую линию О₁О₂ в постоянной точке Р (в соответствии с доказанной теоремой). Эта точка называется полюсом зацепления, её положение на межосевой линии определяется отношением угловых скоростей колёс, т.е. передаточным отношением.

Отрезок общей нормали NN, ограниченной токами А и В и являющийся траекторией общей точки контакта зубьев, называется линией зацепления зубчатой передачи.

Окружности, проходящие через полюс и обозначенные d_W1 и d_W2, называются начальными окружностями. При вращении зубчатых колёс начальные окружности перекрываются друг по другу без скольжения, о чём свидетельствует равенство их окружных скоростей .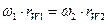

Следует иметь ввиду, что незначительное изменение межосевых расстояний a_n приведёт к изменению и диаметров начальных окружностей, т.к. положение полюса зацепления при этом остаётся неизменным. α_W – носит в дальнейшем название угол профиля – острый угол между линией зацепления и перпендикуляром к межосевой линией, его стандартное значение для эволвентных зацеплений α_W = 20^°.

Эвольвентные окружности и её свойства.

Эвольвентой называется кривая, описываемая любой точкой прямой, перекатываемой без проскальзывания по неподвижной окружности.

Так точка А прямой NN (точки от А₀ до А₈) опишет эвольвенту. Длина дуги окружности, которую проходит точка её контакта с прямой NN, всегда равна длине этой прямой от точки касания с окружностью до эвольвенты (например дуга А₀В₁ = А₁В₁, А₀В₂ = А₂В₂, А₀В₃ = А₃В₃ и т.д.).

Окружность радиусом r_b, по которой перекатывается прямая NN, называется эволютой или основной окружностью, а перекатываемая прямая – производящей прямой. Для построения профиля зуба используется часть эвольвенты.

Свойства эвольвенты:

1. эвольвента не заходит внутрь основной окружности а представляет собой спиральную кривую, начинающуюся от основной окружности и полностью определяющуюся её радиусом;

2. производящая прямая NN является одновременно касательной к основной окружности и нормалью ко всем производимым ею эвольвентам, это свойство вытекает непосредственно из построения эвольвенты;

3. две или семейство эвольвент одной и той же основной окружности эквидистантны. Эквидистантными или равноудалёнными называются две кривые, расстояние между которыми в направлении нормали везде одинаковое, (Р_в) – это шаг по основной окружности;

4. радиус кривизны эвольвенты в любой точке равен длине касательной к основной окружности, проведённой из этой точки. Центр кривизны эвольвенты в данной точке находится на основной окружности. Это свойство так же вытекает непосредственно из построения эвольвенты;

5. с увеличением радиуса r_b основной окружности эвольвента становится более пологой и при 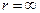обращается в прямую.

Эвольвента и её свойства.

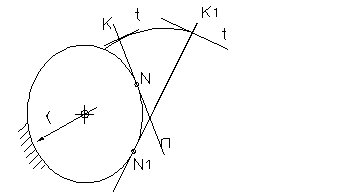
Эвольвента – это след движения точки принадлежащей прямой при её качении по неподвижной окружности без скольжения

Свойства:

- Все нормали в эвольвентах касаются одной и той же основной окружности.

- Все центры кривизны эвольвенты лежат на одной и той же основной окружности.

Основная окружность – это геометрическое место центров кривизны эвольвенты (эволюты).

Эвольвента – симметричная кривая с точкой возврата, лежащей на основой окружности.

Возможность получения удлинённых и укороченных эвольвент.

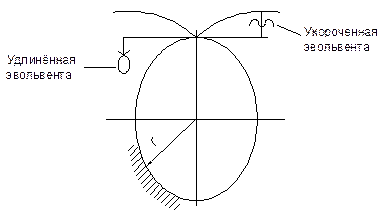
При увеличении r_b эвольвента распрямляется и при 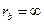становится прямой линией.

Взаимодействие эвольвент.

Рассмотрим взаимодействие эвольвент двух окружностей радиусами r_b1 и r_b2 с центрами О₁ и О₂, вокруг которых могут вращаться эвольвенты 1 и 2.

В первом положении эвольвенты касаются в точке 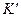. В этой точке они имеют общую нормаль АВ. Эта нормаль является производящей прямой обоих эвольвент и поэтому касается обеих основных окружностей. Из рассмотренного вытекает очень важное свойство эвольвент: у двух сопряжённых эвольвент радиусы кривизны точек касания лежат на общей нормали.

Повернём основную окружность с эвольвентой 1 на некоторый угол 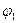вокруг центра О₁. При этом эвольвента 1 окажет давление на эвольвенту 2, это давление 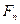может предаваться только по общей нормали к обоим кривым, т.е. по линии АВ. Следовательно общая нормаль является линией давления. Поскольку линия давления не проходит через центр О₂, то вторая основная окружность вместе с эвольвентой 2 повернётся на некоторый угол φ₂. Таким образом, посредством двух эвольвентных профилей можно осуществить передачу движения.

В новом положении эвольвенты соприкасаются в т. 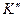, имея общую нормаль АВ. Общая нормаль является геометрическим местом точек касания взаимодействующих эвольвент. Из сказанного следует, что линия зацепления является линией давления.

При повороте эвольвент соответствующие дуги основных окружносте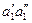й и 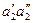равны между собой, поскольку каждая из них равна расстоянию 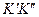по общей нормали, а значит 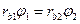. Так как угловые скорости пропорциональны угла поворота, то 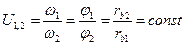, т.е. отношение угловых скоростей двух взаимодействующих эвольвентных профилей обратно пропорционально радиусам их основных окружностей и не зависит от межосевого расстояния этих окружностей.

Начальные окружности перекатываются без скольжения, т.е. эвольвентные профили взаимодействуют различными участками (считая от основания эвольвенты), т.е. дугами различной длины, то их относительное движение происходит со скольжением, чем далее от полюса тем больше скольжение, наибольшее скольжение имеет место у основания эвольвенты. При переходе через полюс изменяется направление скольжения.

Взаимодействие эвольвентных профилей сопровождается трением. Сила трения достигает наибольшего значения вблизи полюса, где скорость скольжения близка к нулю.

Лекция 10.

Методы нарезания зубчатых колёс.

Заготовку зубчатых колёс получают литьём, штамповкой или ковкой, в зависимости от материала, формы и размеров. Существуют два основных метода изготовления зубчатых колёс: метод копирования и метод обкатки.

Метод копирования.

Метод копирования заключается в удалении той части материала заготовки, которая заполняет объём будущей впадины, инструментом с режущим контуром, совпадающим с контуром впадины нарезаемого колеса. После прорезания каждой впадины заготовка поворачивается на угол 360/z. Контур впадины нарезаемого колеса, определяется его параметрами (m, z, mx). С изменением одной из этих характеристик должен быть изменён режущий контур соответствующего инструмента. Колеса, изготовленные методом копирования, нарезаются неточно. Таким образом, данный метод малопроизводителен, неточен и требует большого количества инструмента. При методе обкатки режущему инструменту и заготовке сообщают такое относительное движение, какое имели бы зубчатые колёса в зацеплении. Зацепление производящего колеса с обрабатываемым называют станочным зацеплением. Существуют несколько способов обкатки.

При зубодолблении инструмент (долбяк) совершает возвратно-поступательно движение,, одновременно долбяку и колесу (заготовка) сообщается вращательное движение. Профиль зуба образуется как огибающая последовательных положений зуба долбяка, построенных относительно заготовки.

При нарезании зуба с помощью инструментальной рейки (гребёнки) суппорт с рейкой участвуют в реверсивном движении, при рабочем ходе осуществляется строгание. За время вспомогательного хода заготовка получает перемещение вдоль гребёнки и поворот вокруг своей оси. Это движение осуществляется аналогично процессу зацепления колеса с рейкой.

Более производительным при нарезании колёс с внешним зубчатым венцом считается зубофрезерование с помощь фрез.

Зубья точных зубчатых колёс после нарезания подвергают доводке шевингованием, шлифованием, притиркой или обкаткой.

Шевингование применяется для тонкой обработки незакалённых колёс. Выполняется инструментом – шевером, имеющим вид зубчатого колеса с узкими канавками на поверхности зубьев. Вращаясь в зацеплении с обрабатываемым колесом, шевер снимает режущими кромками канавок волосообразные стружки с зубьев колеса.

Шлифование применяется для тонкой обработки закаленных зубьев. Выполняется шлифовальными кругами способом копирования или обкатки.

Притирка используется для отделки закалённых зубьев колёс. Выполняется притиром – точно изготовленном чугунным колесом с использованием притирочных абразивных паст.

Метод обкатки.

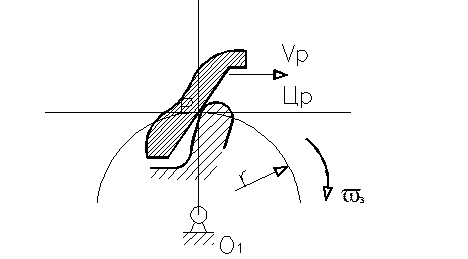
Обкатка применяется для сглаживания шероховатостей на рабочих поверхностях зубьев незакалённых колёс. В течении 1…2 минут зубчатое колесо обкатывается под нагрузкой с эталонным колесом Большой твёрдости.

Основные размеры зубчатых колёс.

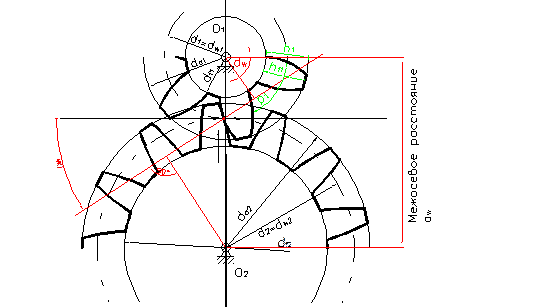
Часть зубчатого колеса, содержащая все зубья, связанные друг с другом прилегающей к ним поверхностью. Тело зубчатого колеса, называется зубчатым венцом.

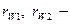радиусы основных окружностей.

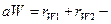межосевое расстояние.

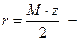радиус делительной окружности.

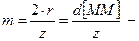модуль [мм].

Модуль – это часть диаметра делительной окружности, приходящейся на 1 зуб.

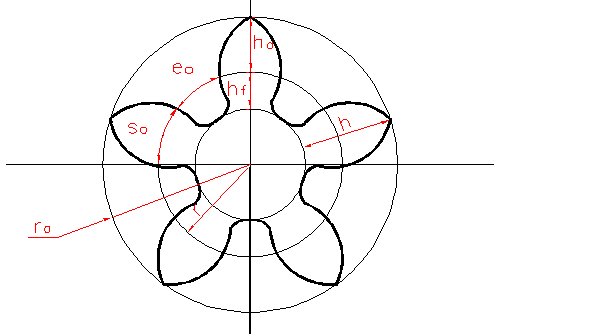
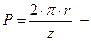шаг – часть длины делительной окружности, приходящейся на 1 круг.

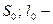ширина впадины.

.

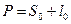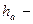высота головки зуба.

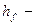высота ножек зуба.

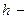полная высота зуба.

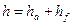
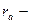радиус окружности головки.

радиус окружности ножек.

.

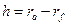Таким образом, окружным делительным модулем 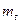зубьев называется линейная величина в 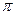раз меньшая делительного окружного шага. Если модуль представить как 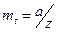, то окружной делительный модуль можно рассматривать как часть диаметра делительной окружности, приходящийся на один зуб. Модуль измеряют в мм. Для пары зацепляющихся колёс модуль должен быть одинаковым. Для обеспечения взаимозаменяемости зубчатых колёс и унификации зуборезного инструмента значение 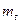гостированы. Из изложенного видно, что диаметр делительной окружности равен произведению числа зубьев на стандартный модуль.

Окружный шаг зубьев по делительной окружности равен сумме толщины зуба и ширины впадины: ; .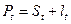

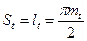Для пары сцепляющихся колёс шаг одинаков. Толщина зубьев 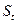и ширина впадины теоретически равны между собой. Практически между зацепляющимися зубьями имеется небольшой боковой зазор.

Основной шаг 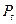измеряется по основной окружности. Из треугольника О₁АР или O₂BР

; ; .

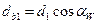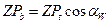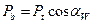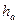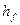Угловым шагом зубьев называется центральный угол окружности в центре зубчатого колеса, равный ?. Делительная окружность делит зуб на головку и ножку, высоты которых соответственно обозначены и . При этом обычно принимают 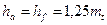, откуда 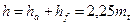. Разница в высоте ножек зубьев одного колеса и высоте головок зубьев другого необходима для образования радиального зазора с: .

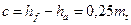Геометрию зубчатого венца характеризуют концентрическими окружностями с центром на оси зубчатого колеса, лежащими в торцевом сечении. Различают делительную 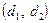, начальную 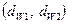, основную 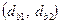, вершин зубьев 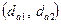, впадин зуба .

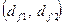Начальными называются окружности, проходящие через полюс П, которые в процессе зацепления перекатываются одна по другой без скольжения. Начальная скорость – центройда относительного движения и зацепления зубчатых колёс в передаче. Под центроидой понимается геометрическое место мгновенных скоростей в относительном профилей двух звеньев. Мгновенный центр скоростей в относительном движении двух профилей – это полюс зацепления.

.

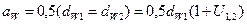Делительной называется окружность, по которой в процессе изготовления зубчатого колеса проводится деление цилиндрической заготовки на z равных частей (технологическая окружность). В нулевых передачах, у которых коэффициент суммы смещений 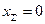и угол зацепления 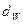равен стандартному углу 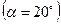профиля зуба исходного контура, делительные окружности совпадают с начальными ( 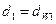, 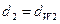). 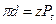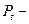Диаметр делительной окружности равен , где окружный шаг зубьев по делительной окружности, т.е. расстояние между одноимёнными профилями соседних зубьев по дуге делительной окружности, z – число зубьев.

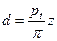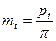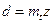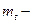Делительная окружность принадлежит отдельно взятому колесу. При изменении межосевого расстояния её диаметр остаётся неизменным ; ; , где окружный диаметральный модуль передачи.

Наибольшее расстояние между торцами звеньев колеса называется шириной венца и обозначается ?. Расчётные окружности прямозубых колёс ; ; .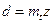

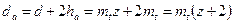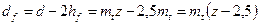Межосевое расстояние прямозубой передачи без смещения: 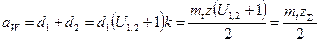, где 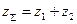. Зная 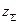определяют число зубьев шестерни 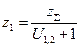и колеса .

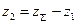Диаметр основной окружности 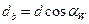, диаметр окружности впадин .

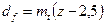Приняв эти выражения, получим 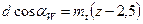; ; 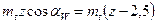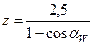, если 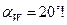, то .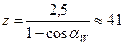

Следовательно, если число зубьев колеса более 41, то диаметр основной окружности меньше диаметра окружности впадин и весь профиль зуба может быть очерчен по эвольвенте. Если же 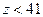, то диаметр основной окружности больше диаметра окружности впадины и только часть профиля зуба, лежащая за пределами основной окружности, очерчен по эвольвенте. Часть профиля зуба, лежащая внутри основной окружности, очерчивается по переходным кривым, не отвечающим требованиям основной теоремы зацепления.

Активная линия зацепления, характерные точки на линии зацепления, профиль зуба.

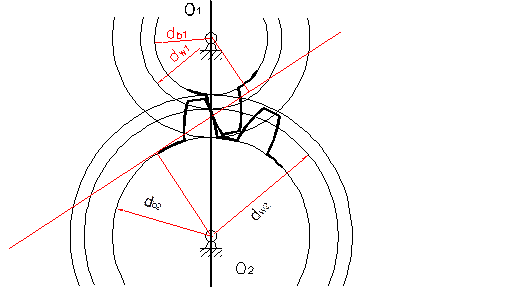
Как указывалось выше. Линией зацепления ЗП является отрезок АВ, который представляет траекторию общей точки контакта двух сопряжённых зубьев за период их зацепления. При этом отрезок АВ определяет предельную длину линии зацепления. При внешнем зацеплении эвольвентные профили являются сопряжёнными только в пределах отрезка АВ линии зацепления, ограниченного точками касания с основными окружностями (точки А и В получены путём восстановления перпендикуляров к производящей прямой соответственно из центров О₁ и О₂). Таким образом, за пределами линии зацепления нарушается основная теорема зацепления. Активной линией зацепления называется отрезок ab (К₁К₂), представляющий собой часть линии зацепления АВ. Активная линия зацепления отсекается на прямой АВ окружностями вершин сопряжённых зубьев. Длину активной линии зацепления будем обозначать буквой .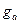

Активной поверхностью зуба называется часть боковой поверхности зуба, на которой происходит взаимодействие с боковой поверхностью зуба парного колеса. Активным профилем зуба называется часть профиля зуба, соответствующая активной поверхности. Профиль головки зуба полностью участвует в зацеплении сопряжённого зуба. Профиль же ножки зуба не весь участвует в зацеплении. Тот участок профиля на котором происходит фактическое касание сопряжённых зубьев, и является его активной частью. Чтобы определить границу активного участка профиля (его верхнюю и нижнюю точки), нужно на ножке зуба найти точку, сопряжённую с вершиной парного зуба.

Чтобы найти активные участки профиля зуба обоих колёс, нужно через начало и конец активной линии зацепления (через точки a и b) провести дуги из центра О₁ радиусом О₁a до встречи с профилем зуба в точке a₁, а через точку b из центра О₂ радиусом О₂b до встречи со своим профилем зуба в точке b₂.

Увеличение активных профилей зубьев возможно вследствие увеличения диаметров окружностей вершин. Однако, если окружность вершин одного из зубчатых колёс будет пресекать линии зацепления за предельными точками А или В, то произойдёт явление интерференции зубьев, при котором профиль головки зуба одного колеса накладывается на профиль ножки второго колеса за пределами линии зацепления. Произойдёт заклинивание колёс.

Коэффициент перекрытия.

Для обеспечения непрерывной безударной работы передачи необходимо, чтобы выход из зацепления одной пары зубьев упреждался входом в зацепление следующей пары зубьев. Это свойство характеризуется коэффициентом перекрытия, которых характеризует плавность работы зубчатой передачи и показывает, какое число зубьев одновременно участвует в перекрытии зацепления.

Теоретически 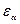может быть равен 1 и это означает что только одна пара зубьев вышла из зацепления, следующая пара сразу же вошла в зацепление. Если 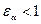, то предыдущая пара зубьев из зацепления вышла, а следующая пара в зацепление не вошла, т.е. передача работает с ударами и её применение недопустимо. Эвольвентная зубчатая передача с прямозубым колесом имеет 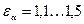, для косозубых колёс коэффициент перекрытия 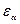увеличивается за счёт коэффициента осевого перекрытия .

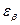Коэффициентом торцевого перекрытия ЗП называется отношение угла торцевого перекрытия зубчатого колеса передачи к его угловому шагу 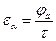, где 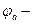угол торцевого перекрытия зубчатого колеса, под которым понимают угол поворота зубчатого колеса от положительного входа зуба в зацепление до выхода его из зацепления; 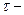угловой шаг передачи.

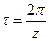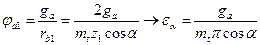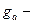; ; длина активной линии зацепления.

; .

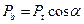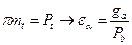Полученное выражение может использоваться только при наличии графических построений зацепления. Для аналитического метода определения 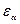воспользуемся рисунком.

; ; ; ; .

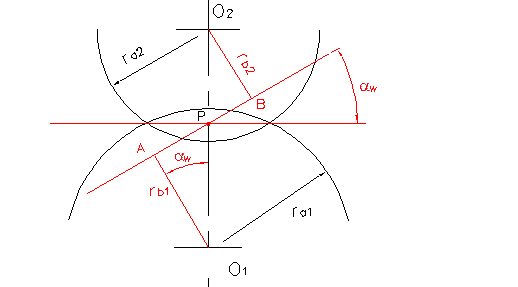
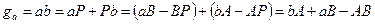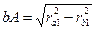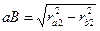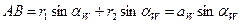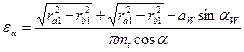В расчётной практике пользуются приближённой формулой: 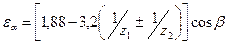; здесь знак + для внешнего, минус для внутреннего зацепления. Величина 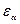зависит от числа зубьев z и угла наклона зубьев 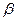. Поэтому выгодно применять колёса с большим числом зубьев или при заданном диаметре d с малым модулем m_t. С увеличением 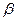растёт окружной шаг P_bt а длина активной линии зацепления 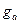остаётся неизменной, при этом 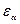уменьшается, что является одной из причин ограничения угла .

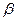Уравнение эвольвенты в полярных координатах.

Точка А – начало эвольвенты.

ОА – линия начала отсчёта углов в полярных координатах.

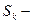радиус кривизны эвольвенты.

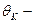полярных угол.

; ; ;

; .

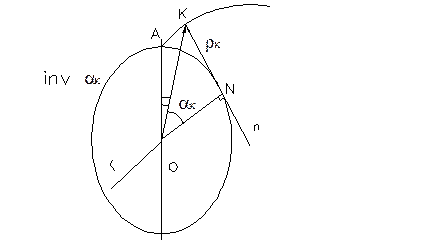
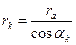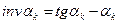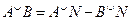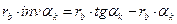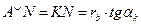Стандартный исходный центр рейки.

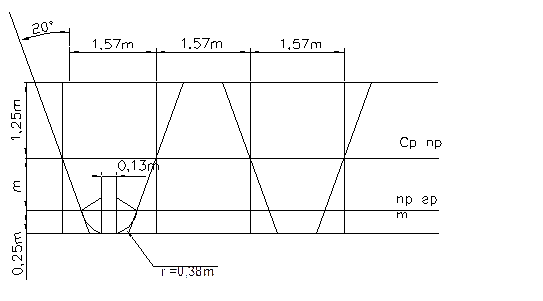
При увеличении числа зубьев до бесконечности, колесо превращается в рейку, а эвольвентный профиль зуба – в прямолинейный, нормальный к линии зацепления.

Строят исходный контур инструментальной зубчатой рейки: проводят линию, принимаемую за среднюю линию (СП) рейки. Вниз от СП последовательно откладывают расстояния 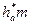и 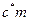( 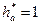, 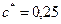). Через них проводят линии граничных точек (ЛГТ) и прямые головок и ножек зубьев рейки. На средней линии (СП) отмечают полюс – точку Р и откладывают расстояния 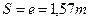(толщину зуба и и ширину впадины соответственно). Через полученные точки на средней линии проводят наклонные линии под углом 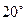к вертикали.

Головки зубьев рейки на углах скругляют сопрягающими дугами. Закругление начинается от линии ЛГТ, отстающей от средней прямой на расстояние m. Центр закругления 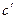находится на пересечении двух прямых: перпендикуляра 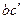к профилю зуба рейки, проведённому и точке b и перпендикуляра dc к прямой головок рейки, проведённому из точки d. Для нахождения точки d необходимо отложить be = ed. Радиус 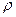закругления головок зубьев рейки равен 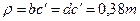. По окончании построения левых и правых закруглений головки зуба рейки делают проверку: расстояние между центрами этих закруглений должно составлять 0,13m.

Лекция 11.

Характерные точки на линии зацепления.

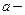последняя рабочая точка над линией зацепления.

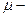характеризует со средней прямой.

Р – полюс зацепления.

N – точка, до которой выдерживается основной закон зацепления.

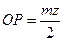; ОР – радиус делительной окружности.

1. Ра > PA: при этом условии возникает явление подреза. Оно характеризуется укорочением головки зуба и утоньшением ножки зуба.

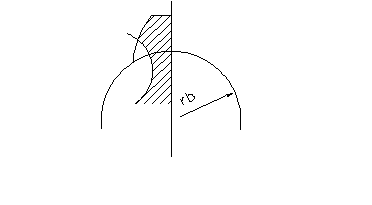
2. Ра = РА; при этом условии подреза нет.

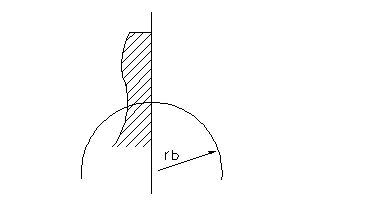
3. Ра < РА.

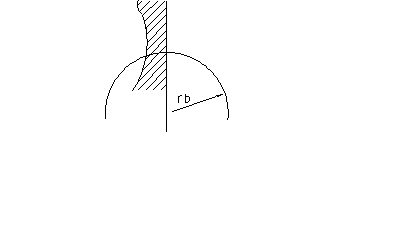
Влияние числа зубьев на подрез.

ЛЗ – линия зацепления.

Уменьшение числа зубьев ведёт к опасности возникновения подреза.

1. 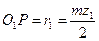; Ра < РА

2. 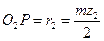; Ра > PA (появляется подрез)

Минимальное число зубьев, нарезаемых без подреза, если а совпадает с А.