Математическая модель силового трансформатора

Цель работы:

- изучить схемы замещения силового трансформатора;

- изучить математические модели различных схем замещения силового трансформатора;

- научиться определять основные параметры силового трансформатора;

Основные теоретические положения:

Трансформатором называют статическое электромагнитное устройство, имеющее две (или более) индуктивно связанные обмотки и предназначенное для преобразования посредством электромагнитной индукции одной системы переменного тока в другую систему переменного тока. При этом число фаз, форма кривой напряжения (тока) и частота остаются неизменными.

Принцип действия трансформатора основан на явлении электромагнитной индукции. При подключении первичной обмотки к источнику переменного тока c напряжением u1 в витках этой обмотки протекает переменный ток i1, который создает в магнитопроводе переменный магнитный поток Ф. Замыкаясь на магнитопроводе, этот поток сцепляется с обеими обмотками (первичной и вторичной) и индуктирует в них ЭДС:

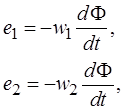(1)

где w₁ и w₂ – число витков в первичной и вторичной обмотках трансформатора.

При подключении нагрузки к выводам вторичной обмотки трансформатора под действием ЭДС е₂ в цепи этой обмотки создается ток i₂, а на выводах вторичной обмотки устанавливается напряжение u₂.

Если взять за основу математической модели трансформатора так называемый идеальный трансформатор с коэффициентом трансформации 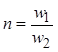, для которого относительная магнитная проницаемость равна бесконечности и ток намагничивания равен нулю, то добавлением к нему элементов, учитывающих основные паразитные эффекты, можно получить полную схему замещения трансформатора (рис 1).

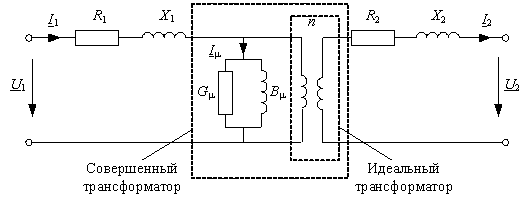
Рис. 1. Полная Т-образная схема замещения трансформатора

Во многих случаях пользуются приведенной Т-образной схемой замещения трансформатора (рис. 2). Получается она приведениям сопротивлений вторичной обмотки к напряжению первичной обмотки по соотношениям:

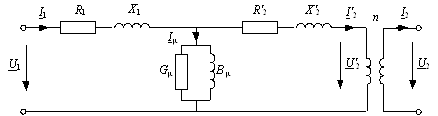
Рис. 2. Приведенная Т-образная схема замещения трансформатора

где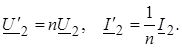

Обычно для силовых трансформаторов более целесообразна так называемая Г-образная схема замещения, элементы которой имеют простой физический смысл и могут быть вычислены или измерены.

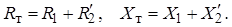
Рис. 3. Г-образная схема замещения трансформатора

Сопротивления и проводимости Г-образной схемы замещения трансформатора, приведенные к напряжению обмотки первичного напряжения, определяются по формулам:

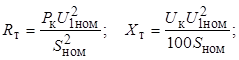
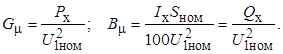
Моделирование элементов схем электрических сетей при использовании специальных программ для расчета их режимов работы удобно выполнять по П-образным схемам замещения.

Из уравнения четырехполюсника

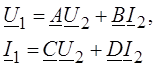
имеем:

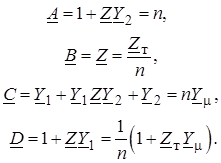
Из полученных соотношений можно найти параметры П-образной схемы замещения трансформатора:

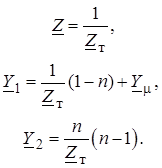
Г-образная схема замещения трансформатора в отличие от П-образной схемы замещения ЛЭП является несимметричной, т. е. Y₁ ≠ Y₂.

Практическое задание:

Построить внешнюю характеристику силового трансформатора по его Г-образной полной и упращенной математическим моделям при неизменном коэффициенте мощности. Сравнить полученные характеристики. Исходные данные приведены в таблицах 2.1 и 2.2.

Таблица 2.1 – Исходные данные

Вариант №	Тип трансформатора	Коэффициент мощности
	ТМН-6300/110	0,7
	ТРДН-25000/110	0,75
	ТМН-2500/110	0,8
	ТМН-6300/110	0,85
	ТДН-16000/110	0,9
	ТРДН-40000/110	0,65
	ТДН-10000/110	0,7
	ТДЦ-80000/110	0,75
	ТДН 25000/110	0,8
	ТДН 63000/110	0,85
	ТДН-16000/110	0,9
	ТДН-10000/110	0,65
	ТДЦ-80000/110	0,75
	ТМН-2500/110	0,8
	ТРДН-25000/110	0,85
	ТДН 80000/110	0,9
	ТМН-6300/110	0,65
	ТРДН-40000/110	0,75
	ТДЦ-80000/110	0,8
	ТДН 25000/110	0,85
	ТДН-10000/110	0,9
	ТДН 80000/110	0,65
	ТДН 63000/110	0,75
	ТРДН-25000/110	0,8
	ТДН 80000/110	0,85
	ТРДН-40000/110	0,9
	ТДН-16000/110	0,65
	ТДН 63000/110	0,75
	ТМН-2500/110	0,8
	ТДН 25000/110	0,85

Таблица 2.2 – Параметры силовых трансформаторов

Тип	ТМН-6300/110	ТДН-10000/110	ТДН-16000/110	ТРДН-25000/110	ТРДН-40000/110	ТДЦ-80000/110	ТМН-2500/110	ТДН 25000/110	ТДН 63000/110	ТДН 80000/110
Sном, МВА	6,3						2,5
UK, %	10,5	10,5	10,5	10,5	10,5		10,5	10,5	10,5	10,5
Iх, %	0,8	0,9	0,7	0,65	0,55	0,6	1,5	0,65	0,5	0,45
∆PK, МВт	0,047	0,058	0,085	0,12	0,17	0,31	0,022	0,12	0,245	0,310
∆Pх, МВт	0,008	0,014	0,018	0,025	0,034	0,085	0,0055	0,025	0,05	0,058
UBH
UHH	6,6; 11	6,6; 11	6,6; 11	6,3; 10,5	6,3; 10,5	6,3;10,5	6,6; 11	38,5	38,5	38,5

Методика решения задачи:

1) Определим параметры силового трансформатора

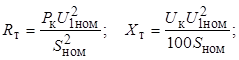
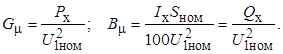
Математическая модель Г-образной схемы замещения имеет вид

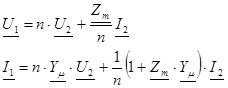, (ХХ)

где n – коэффициент трансформации трансформатора;

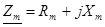- сопротивление трансформатора;

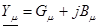- проводимость трансформатора.

Примем ток I₂ фазным, тогда первое уравнение системы (ХХ)

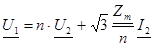
Следовательно,

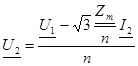
Разделим уравнение на действительную и мнимую часть и получим систему уравнений

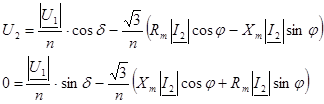
Примем cosφ = 0,7, тогда sinφ = 0,7. Изменяя значения тока вторичной цепи I₂=0..I_2ном построим внешнюю характеристику силового трансформатора.

2) Упрощенная математическая модель имеет вид

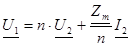, (ХХ)

где n – коэффициент трансформации трансформатора;

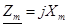- сопротивление трансформатора.

Разделим уравнение на действительную и мнимую часть и получим систему уравнений

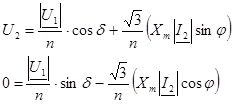
Примем cosφ = 0,7, тогда sinφ = 0,7. Изменяя значения тока вторичной цепи I₂=0..I_2ном построим внешнюю характеристику силового трансформатора.

Сравним внешние характеристики различных математических моделей силовых трансформаторов.

Расчётная работа 3.