Некоторые применения рядов Тейлора

1. Приближенное вычисление значений функции

Допустим, что нам известны значения самой функции f(x) и ее последовательных производных в некоторой точке 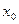и f(x) в окрестности этой точки разлагается в ряд Тейлора. Тогда точное значение функции f(x) в любой точке этой окрестности может быть вычислено по ряду Тейлора, приближенное ее значение по частичной сумме этого ряда.

Возникающую при этом ошибку можно оценивать либо опираясь на теорему об оценке остаточного члена, либо непосредственно оценивая остаток ряда. Если, например, получающийся числовой ряд знакочередующийся, то это делается при помощи теоремы Лейбница; в случае знакоположительного ряда стараются подобрать другой ряд (обычно геометрическую прогрессию), элементы которого больше элементов остатка и, сумму которых мы можем найти.

На практике оценка остатка ряда оказывается более удобной, так как оценка остаточного члена предполагает знание производной нужного нам порядка во всем рассматриваемом интервале. Часто можно получить разложение функций в ряды, вообще не отыскивая производных, а комбинируя известные нам ряды.

Рассмотрим примеры

1) Имеем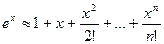

Производя вычисления по этой формуле в интервале [0,M], где М – любое число и учитывая, что 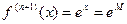по теореме об оценке остаточного члена получим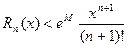

Оценка неудобна тем, что сюда входит величина 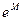. Кроме того, она может оказаться слишком завышенной, так как установлена для всего интервала.

При М=1 получим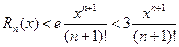

Подсчитаем, например, сколько нужно взять элементов ряда, чтобы получить число е с точностью до 0,00001.

Здесь x=1 и должно быть 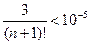. Неравенство справедливо при n=8

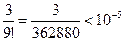. Чтобы получить число е с этой точностью надо в сумме

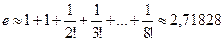все слагаемые брать с точностью 0,00001 во избежание накопления ошибок при арифметических действиях. В результате нашли число е с шестью верными знаками.

Покажем теперь, как можно оценивать ошибку 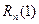, пользуясь всем рядом для .

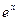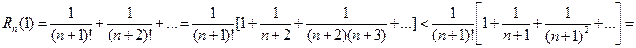
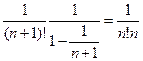. Итак мы получили оценку ошибки 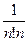, то есть почти в три раза более точную, чем найденную выше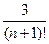

2) Вычислить значение функций sinx и cosx при помощи их разложений в ряды.

Приближенные формулы отличаются здесь очень высокой точностью, а ошибка легко оценивается с помощью теоремы Лейбница.

Положим в разложении функции sinx последовательно n=1,2,3. Считая х>0 получим

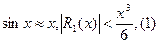
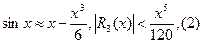
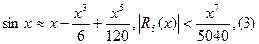
(1) и (3) дают значение функции с избытком, а (2) - с недостатком.

Замечание

Для получения значений sinx с точностью 0,00001 следует пользоваться

(1) в интервале (0<x<0,08)

(2) в интервале (0,08<x<0,4)

(3) в интервале (0,4<x<0,9)

На следующем рисунке представлены графики функций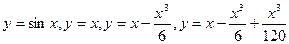

Аналогично получаем приближенные формулы для cosx

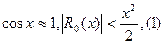
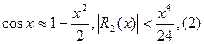
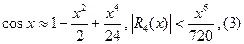
(1) и (3) дают значение функции с избытком, а (2) - с недостатком.

На следующем рисунке представлены графики функций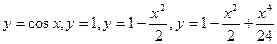

1. Интегрирование функций

Допустим, что нужно найти интеграл 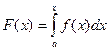, причем известно разложение функции f(x) в ряд Тейлора, а пределы интегрирования лежат внутри интервала сходимости ряда. Тогда можно интегрировать ряд поэлементно. В результате получаем ряд Тейлора для функции F(x), имеющей тот же радиус сходимости, что и ряд для f(x). Если 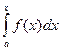выражается через элементарную функцию F(x), то тем самым находим ее разложение в ряд Тейлора. Если же 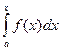в элементарных функциях не выражается, то найденный ряд может служить выражением неэлементарной функции F(x) через самые простые элементарные функции – степенные, но уже бесконечным выражением.

Замечание Зная оценку остаточного члена ряда для f(x) можно на основании теоремы об оценке интеграла можно оценить и остаточный член ряда для интеграла F(x).

Примеры:

1) Пусть дан интеграл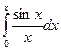

Раскладывая sinx в ряд и деля на x, получаем

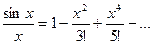интервал сходимости 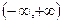. Интегрируем

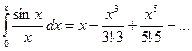
Этот ряд не сходится ни к одной элементарной функции; он является аналитическим заданием новой функции, посредством бесконечного числа операций.

Функция 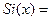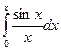(интегральный синус) встречается в теоретической физике. С помощью приведенного ряда составлены подробные таблицы.

2) При изучении теории вероятностей важную роль играет функция

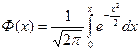- функция Лапласа или интеграл вероятностей. Этот интеграл не выражается в элементарных функциях.

Раскладываем функцию 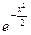, заменяя x на 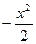. Получаем разложение

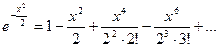тогда для функции

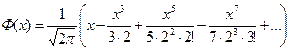
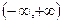Интеграл сходится быстро при |x|<1

3) Вычислить интеграл 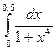. В общем случае неопределенный интеграл выражается в элементарных функциях. Однако это выражение очень сложно и неудобно для вычислений.

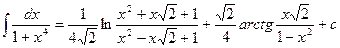
В то же время, разложив подынтегральную функцию в ряд

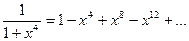получаем

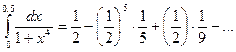
Если ограничиться двумя первыми элементами ряда

(при этом ошибка не превосходит ,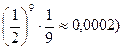

то