Означення. Два цілих числа і називаються конгруентними за модулем , якщо їхня різниця ділиться на .

Відношення конгруентності записується у виді: 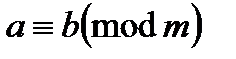, , 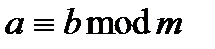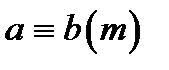. Замість знака конгруентності часто використовується знак рівності. Числа, що мають однакові остачі від ділення на 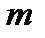, конгруентні за модулем .

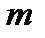Стандартні значення лишків за модулем 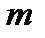належать множині 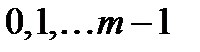(система найменших додатних лишків).

Лишок суми за модулем 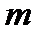дорівнює сумі лишків, зведеної, якщо необхідно, ще раз за модулем 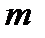. Аналогічну властивість має лишок добутку.

18. Кільце класів лишків.

Відношення конгруентності дозволяє розбити множину 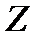цілих чисел на класи. Елементи одного класу мають однакові лишки за модулем 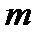. Очевидно, класи не перерізаються. Кожному класу відповідає один найменший додатний лишок і навпаки.

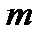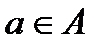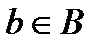Лишок суми або добутку за модулем елементів і не залежить від вибору цих елементів, а залежить лише від вибору класів 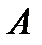і .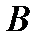

Можна побудувати кільце, елементами якого є класи, а операції виконуються через дії над відповідними найменшими додатними лишками.

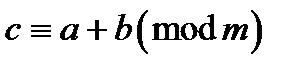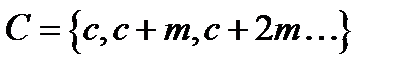Наприклад, якщо , те клас, що містить , є множиною виду . Оскільки множина 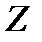цілих чисел є кільцем, то наша відповідність між класами і лишками 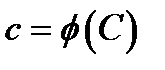є гомоморфізмом кілець. Образ цього гомоморфізму (кільце класів лишків за модулем 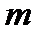) називається фактором-кільцем кільця цілих чисел за модулем 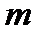і звичайно позначається 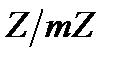. Зауважимо, що нулем у кільці лишків у кільці 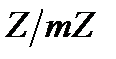є клас .

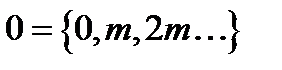При зашифруванні інформації використовуються взаємно однозначні перетворення даних. Для знаходження обернених елементів у кільці 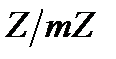можна використовувати розширений алгоритм Евкліда

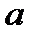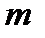Алгоритм Евклида показує, що для взаємно простих чисел і завжди існує число 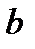таке, що 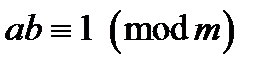. Таке число називається оберненим до 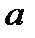за модулем 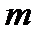і позначається .

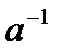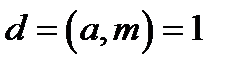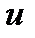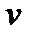Дійсно, якщо , то відносно і розв'язуване рівняння 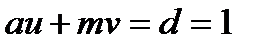. Приводячи за модулем 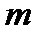обидві частини зазначеної рівності, одержимо порівняння 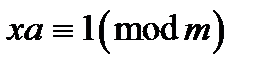, тобто .

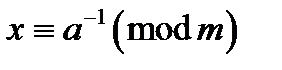Якщо модуль є простим числом 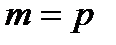, усі ненульові лишки за модулем 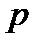взаємно прості з модулем. Отже, кільце .

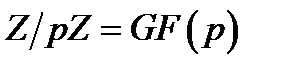19. Кільце класів лишків многочленів над полем.

За аналогією з кільцем лишків за модулем 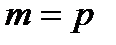, можна побудувати кільце лишків поліномів за модулем нормованого незвідного полінома 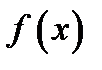над полем .

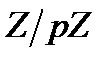Для цього досить розглянути множину залишків від ділення всіх поліномів із коефіцієнтами з 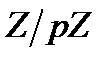та помітити, що розширений алгоритм Евкліда може бути переформульований для розв’язування рівняння аналогічного 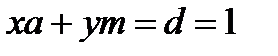, а саме: .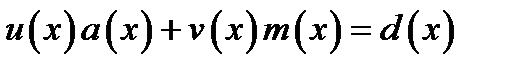

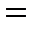
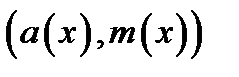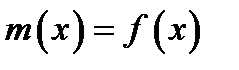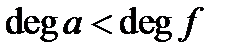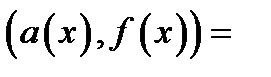
Якщо покласти , то, при , 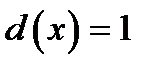і співвідношення 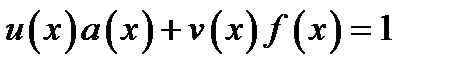, після зведення за модулем 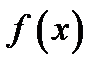дає 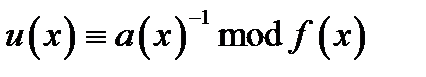. Тому всі ненульові елементи нашого кільця оборотні тобто воно є полем.

Оскільки коефіцієнти поліномів обчислюються за правилами арифметики 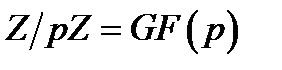, то число 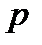є характеристикою нашого поля 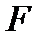. Очевидно, що кількість елементів 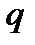поля 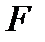дорівнює кількості поліномів, степеня меншої .

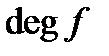Для визначення 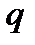зауважимо, що набору коефіцієнтів кожного полінома степеня меншого 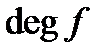, відповідає вектор, кількість координат якого дорівнює 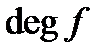. Кожна координата може приймати лишь значення 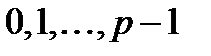. Отже, 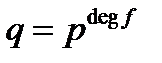. Таким чином, .

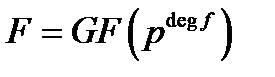Довільний вектор можна розглядати як набір коефіцієнтів деякого полінома. При цьому сумі поліномів буде відповідати сума зазначених векторів. Результатом добутку векторів є вектор коефіцієнтів залишку від ділення добутку поліномів на .

У підсумку, елементи поля 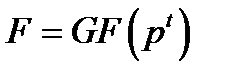можна розглядати як 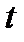- вимірні вектори з координатами з підполя .

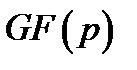Число 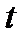називається степенем розширення .

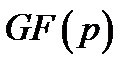Елемент 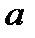поля 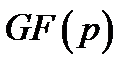представляється в поле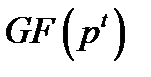 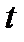- вимірним вектором (розширеним числом) виду .

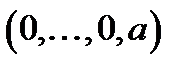20. Функція Ейлера та її властивості.

Порядки чисел за модулем 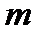різні. Існують числа, що є порядком одночасно для всіх чисел, взаємно простих с. 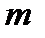Одне з них дорівнює значенню функції Ейлера 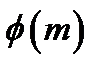, що визначається як число чисел, взаємно простих з .

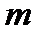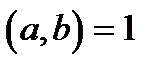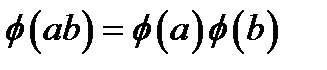Функція Ейлера є мультиплікативною: якщо , те і .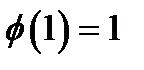

Нехай 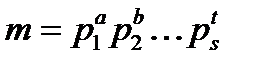, тоді .

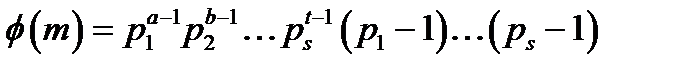Число 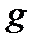називається первісним коренем (первісним елементом) за модулем 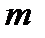, якщо його порядок за модулем 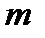дорівнює .

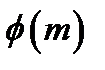При 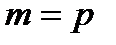первісні корені завжди існують.

Відомо, що в кожному скінченному полі також існує первісний елемент (генератор поля). Степені первісного елемента 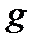представляють усі ненульові елементи поля.

Зокрема, якщо 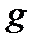первісний елемент поля 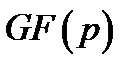, то конгруенція 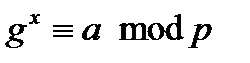розв'язувана для ненульових лишків 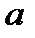за модулем .

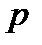Показник 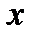у цій конгруенції називається дискретним логарифмом числа 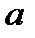за основою 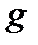. Дискретні логарифми часто називають індексами і позначають 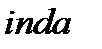або .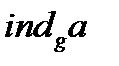

21. Теореми Ейлера і Ферма.

Теорема Ейлера. Якщ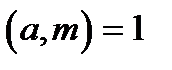о , то .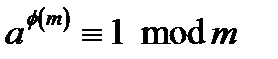

З теореми Ейлера випливає

Мала теорема Ферма: 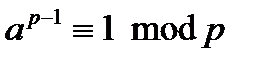, де 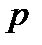- просте, .

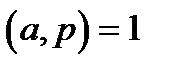Ці теореми інтенсивно використовуються в асиметричній криптографії і, крім того, дуже корисні для скорочення обчислень.

Як наслідок, з теореми Ейлера випливає, що елемент 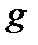є первісним коренем за модулем 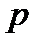тоді і тільки тоді, коли виконуються співвідношення: 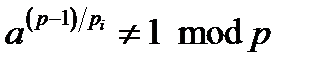, де .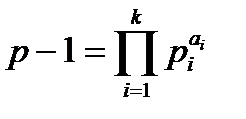

Зауважимо, що в кожному скінченному полі 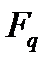, при 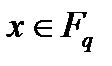, , 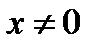виконується співвідношення 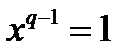. Це зв'язано з тим, що число 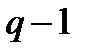є порядком мультиплікативної групи поля.

Щоб врахувати значення 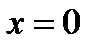, помножимо обидві частини зазначеного співвідношення на 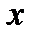. Одержимо, що для будь-якого елемента 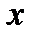кінцевого поля вірне співвідношення .

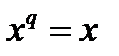Нагадаємо, що розширення скінченного поля може бути представлене як кільце лишків многочленів за модулем незвідного многочлена, 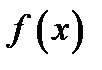над простим полем: .

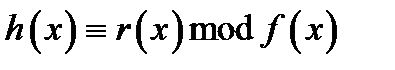Для деяких незвідних многочленів послідовність 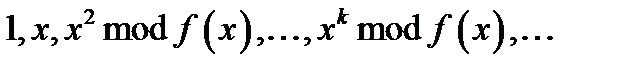пробігає всі можливі лишки, тобто всі елементи поля. Такі многочлени називаються примітивними.

22. Лінійні конгруенції.

Конгруенції виду 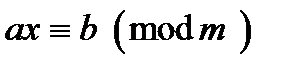можуть мати декілька розв’язків, мати єдиний розв’язок або не мати розв’язків взагалі.

Якщо 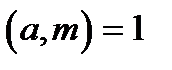, то розв’язок єдиний: .

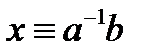Відзначимо, що якщо модуль і коефіцієнти конгруенції 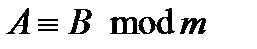розділити або помножити як цілі числа на одне й те саме число, те отримана конгруенція буде істинною. Це випливає з того, що якщо 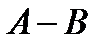ділиться н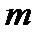а , а 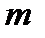ділиться на 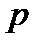, те 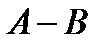ділиться на .

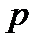Теорема. Розв’язки конгруенції 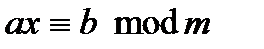існують тоді і тільки тоді, коли 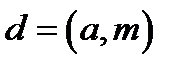ділить .

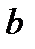У цьому випадку, крім вихідної конгруенції, розв'язувані конгруенції виду 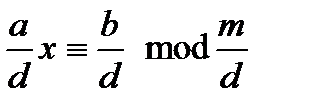з єдиним розв’язком .

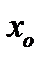Очевидно, всі розв’язки вихідної конгруенції в діапазоні 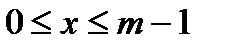є числами виду , .

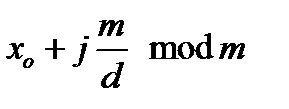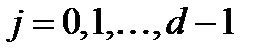Зокрема, якщо 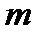просте, то конгруенція 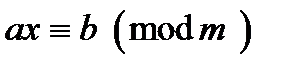має не більш одного розв’язку.

23. Китайська теорема про остачі.

Нехай числа 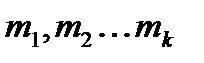попарно взаємно прості і 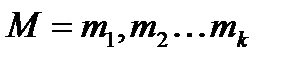. Тоді існує єдиний за модулем 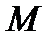розв’язок системи порівнянь , .

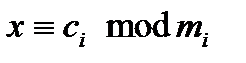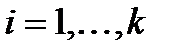При цьому, 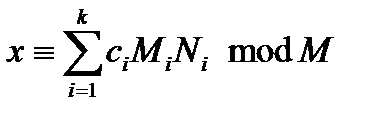, де , .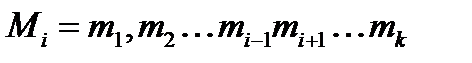

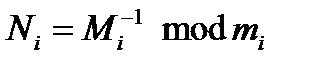Дійсно, у зазначеному вирзі для 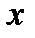, один доданок порівнянний з 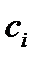за модулем 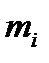, а всі інші порівнянні з нулем.

Коефіцієнти можна обчислити заздалегідь і розв’язувати кілька систем, підставляючи їхні праві частини в лінійну форму.

Китайська теорема про остачі показує, що розв’язок конгруенції 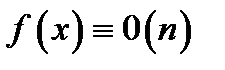можна знайти, якщо знати розв’язки цієї конгруенції за модулями, рівними степеням простих чисел, що входять у канонічний розклад числа 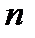на співмножники.