Параметры затухания колебаний

Затухание колебаний характеризуют несколькими параметрами. Во-первых, коэффициент затухания, который характеризует уменьшение амплитуды со временем, согласно формуле (15.4). Пусть за некоторое время τ, называемое временем релаксации, амплитуда уменьшилась в e = 2,72 раза, тогда 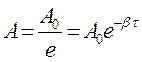, откуда 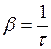. Коэффициент затухания характеризует уменьшение амплитуды колебаний со временем и равен величине, обратной времени релаксации.

Во-вторых, параметром затухания является логарифмический декремент. По определению он равен логарифму отношения амплитуд двух соседних колебаний:

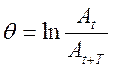, (15.5)

где 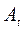– амплитуда в момент времени t, 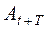– амплитуда через один период .

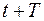Установим связь между логарифмическим декрементом и коэффициентом затухания 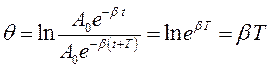, то есть 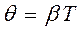. Используя это соотношение уравнение для амплитуды (15.4) можно записать как функцию числа совершенных колебаний N. Подставив время 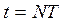и коэффициент затухания 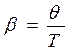, получим 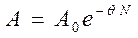. Отсюда видно, что логарифмический декремент характеризует уменьшение амплитуды в зависимости от числа колебаний и равен величине, обратной числу колебаний, в течение которых амплитуда уменьшается в е = 2,72 раза.

Логарифмический декремент характеризует потери энергии. Полная энергия колебаний равна 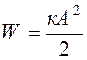, или 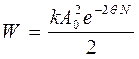. Потери энергии за малое число колебаний определим, дифференцируя функцию энергии 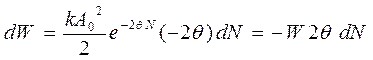. Примем число совершенных колебаний равное половине колебания 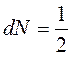и получим 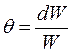. То есть, логарифмический декремент равен относительным потерям энергии за половину периода.

Амортизаторы вагона

На железнодорожном транспорте для смягчения ударных сил применяют рессорное подвешивание вагонов, локомотивов. Но чтобы колебания, вызванные ударом, например стыка рельс, не продолжалось слишком долго, применяют для затухания колебаний амортизаторы. На грузовых вагонах роль амортизаторов выполняют листовые рессоры, а на пассажирских – гидравлические амортизаторы.

Рассмотрим затухание колебаний вагона на листовых рессорах. В рессорах между листами возникают силы сухого трения F_тр = μN, где N – сила сжатия листов рессоры. Силы трения почти постоянны по величине, только меняют направление с изменением направления скорости скольжения трущихся поверхностей. Они не зависят от скорости скольжения листов. Представим рессору вагона в виде пружины и амортизатора из трущихся листов, соединенных параллельно (рис. 15.2а). Приложим внешнюю возрастающую силу F к рессоре. До тех пор, пока эта сила не превысит силу трения скольжения листов, смещения листов рессоры не будет (рис 15.2,б). Только при дальнейшем увеличении внешней силы F начнется скольжение. Деформация рессоры х, согласно уравнению равновесия 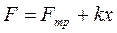, будет возрастать по линейному закону (линия 1–2). Достигнув для данной силы F максималь
ной деформации, 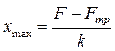, листы перестанут скользить.

Теперь начнем уменьшать внешнюю силу с тем, чтобы началось смещение листа рессоры в противоположном направлении. Автоматически сила трения покоя сначала уменьшится до нуля, а потом изменит направление. Но скольжения не будет до тех пор (линия 2–3), пока сила упругости не превысит разности между внешней силой и силой трения скольжения 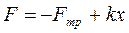. При дальнейшем уменьшении внешней силы до нуля рессора не вернется в исходное положение на величину остаточной деформации 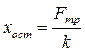. После смены направления внешней силы деформация рессоры будет происходить по линии х_ост – 4.

При колебаниях вагона на рессорах сила действия на рессору будет циклически изменяться, а график F(x) примет вид петли. Ее называют петлей гистерезиса. Так как, согласно графическому смыслу, работа силы равна площади графика «сила–смещение» F(x), то разность работ растяжения и сжатия будет равна площади петли гистерезиса. Эта разность работ равна потерям энергии колебаний за один период колебаний. Площадь петли гистерезиса можно оценить как площадь параллелограмма: ΔW = 2 x_max2F_тр. В свою очередь, сила трения равна произведению коэффициента трения скольжения на силу сжатия листов рессоры, которая практически равна силе тяжести вагона: F_тр=μmg.

По физическому смыслу логарифмического декремента, потери энергии за период можно определить как ΔW=2Wθ. Подставив энергии упругой деформации 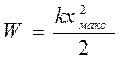, получим значение логарифмического декремента колебаний 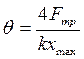. Сопоставив, получим формулу для расчета логарифмического декремента

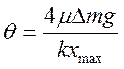. (15.6)

По этой же формуле можно рассчитать параметры рессоры при выбранном значении логарифмического декремента.