Экспоненциальное сглаживание с учетом одновременно тренда и сезонности (метод Винтерса)

Метод Хольта обобщается для временных рядов, содержа­щих наряду с трендом ярко выраженную сезонную компонен­ту. Новый метод линейного и сезонного экспоненциального сгла­живания - метод Винтера - является трехпараметрическим, так как включает три сглаживающие константы. Он содержит три уравнения: к двум уравнениям, сглаживающим наблюде­ния и тренд, добавляется уравнение для сглаживания сезонных изменений.

6.5.1. Метод Винтерса – первый способ

Построение модели Винтера первым способом, не содержит в себе не каких сложностей и во многом схож с алгоритмом построения модели Хольта.

Шаг 1. Установим галочку на пересечении строки Linear trend (Линейный тренд) и столбца Additive (Аддитивно).

Шаг 2. В опции Season components Lag ___ (Лаг сезонной компоненты) укажем значение равное 4 (т.к. длина волны составляет 4 квартала).

Шаг 3. Проведем поиск параметров модели на сетке решений, для этого обратимся к вкладке Grid search нажмем кнопкувкладку Perform grid search. Результаты оценки представим в таблице 6.6.

Таблица 6.6 - Варианты поиска для модели Винтерса ряда среднедушевых денежных доходов населения на сетке решений при а₁ = 0 и y₁=0 индекс сезонности равен 1 (приведена часть исходной таблицы)

	Alpha	Delta	Gamma	Mean Error	Mean Abs Error	Sums of Squares	Mean Squares	Mean % Error	Mean Abs Error
	0,4	0,9	0,4	36,712	197,157		60275,46	-0,104	6,132
	0,4	0,8	0,4	37,788	197,938		62206,26	-0,092	6,072
	0,4	0,9	0,6	30,107	205,065		62235,44	-0,001	6,469

Согласно полученным результатам с установленными параметрами наилучшими признаны 4 модели.

Воспользуемся оцененными параметрами по моделям и рассчитаем прогнозы на 2006г. (результаты представим в таблице 6.7).

Таблица 6.7 – Прогнозные значения по экспоненциальным моделям среднедушевых денежных доходов населения метод Винтерса (первый способ)

Варианты моделей	I/2006	II/2006	III/2006	IV/2006	% средней относительной ошибки
Фактические значения	7873,0	9575,8	9988,2	-	-
Alpha=0,4 Delta=0,9 Gamma=0,4 (а1 = 0 и y1=0)	8337,92	9366,02	9730,30	11140,20	6,13
Alpha=0,4 Delta=0,8 Gamma=0,4 (а1 = 0 и y1=0)	8368,49	9366,86	9754,64	11136,33	6,07
Alpha=0,4 Delta=0,9 Gamma=0,6 (а1 = 0 и y1=0)	8393,16	9461,03	9850,54	11295,20	6,47

6.5.2. Метод Винтерса – второй способ

Шаг 1. Воспользуемся установками из пункта 6.5.1 и добавим в поле Initial trend значение а₁ = 156,418.

Шаг 2. Установим галочку в опции User-def. initial value (Установка значение пользователем) и укажем значение первого уровня ряда y₁=1259,1.

Шаг 3. Найдем на сетке решения оптимальные значения сглаживающих констант для этого обратимся к вкладке Grid search нажмем кнопкувкладку Perform grid search. Результаты оценки представим в таблице 6.8.

Таблица 6.8 - Варианты поиска для модели Винтерса ряда среднедушевых денежных доходов населения на сетке решений при а₁ = 156,418 и y₁=1259,1 индекс сезонности равен 1 (приведена часть исходной таблицы)

	Alpha	Delta	Gamma	Mean Error	Mean Abs Error	Sums of Squares	Mean Squares	Mean % Error	Mean Abs Error
	0,3	0,9	0,5	64,752	182,265		49356,45	1,223	5,106
	0,3	0,9	0,4	74,993	178,374		49954,69	1,402	4,926
	0,3	0,9	0,8	47,060	189,521		51077,67	0,908	5,509

Прогнозы на четыре шага вперед по трем моделям представим в таблице 6.9.

Таблица 6.9 – Прогнозные значения по экспоненциальным моделям среднедушевых денежных доходов населения метод Винтерса (второй способ)

Варианты моделей	I/2006	II/2006	III/2006	IV/2006	% средней относительной ошибки
Фактические значения	7873,0	9575,8	9988,2	-	-
Alpha=0,3 Delta=0,9 Gamma=0,5 (а1 = 156,418 и y1=1259,1)	8284,16	9344,05	9705,14	11145,25	5,11
Alpha=0,3 Delta=0,9 Gamma=0,4 (а1 = 156,418 и y1=1259,1)	8251,06	9290,60	9637,92	11063,27	4,93
Alpha=0,3 Delta=0,9 Gamma=0,8 (а1 = 156,418 и y1=1259,1)	8360,62	9466,90	9855,04	11327,90	5,51

Сравнивая результаты построения моделей Винтерса можно сделать вывод, что второй способ дает лучшие результаты, т.к. процент средней относительной ошибки получен значительно ниже.

Тесты для самоконтроля

1) Для описания динамического ряда с помощью экспоненциального сглаживания содержащего тренд составляющую используют:

а) метод Брауна

б) метод Хольта

в) метод Винтера

2) Для описания динамического ряда с помощью экспоненциального сглаживания содержащего тренд и сезонную составляющую используют:

а) метод Брауна

б) метод Хольта

в) метод Винтера

3) Для описания динамического ряда с помощью экспоненциального сглаживания не содержащего тренд и сезонную составляющую используют:

а) метод Брауна

б) метод Хольта

в) метод Винтера

4) Следующее уравнение 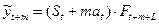используется для прогноз на m периодов вперед при:

а) простом экспоненциальном сглаживание

б) экспоненциальном сглаживании с учетом тренда и сезонности

в) экспоненциальном сглаживании с учетом тренда

5) Следующее уравнение 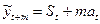используется для прогноз на m периодов вперед при:

а) простом экспоненциальном сглаживание

б) экспоненциальном сглаживании с учетом тренда и сезонности

в) экспоненциальном сглаживании с учетом тренда

6) Приведенные выражения S_t=ay_t+(l-a)(S_t-1+а_t-1), а_t=g (S_t-S_t-1)+(1-g)а_t-1 используются при:

а) однопараметри­ческий методе экспоненциального сглаживания

б) двухпараметри­ческий методе экспоненциального сглаживания

в) трехпараметри­ческий методе экспоненциального сглаживания

7) Приведенные выражения S_t=a(y_t/F_t-L)+(1-a)(S_t-1+а_t-1), F_t=d(y_t/S_t)+(1-d)F_t-L, а_t=g(S_t-S_t-1)+(1-g)а_t-1 используются при:

а) однопараметри­ческий методе экспоненциального сглаживания

б) двухпараметри­ческий методе экспоненциального сглаживания

в) трехпараметри­ческий методе экспоненциального сглаживания

8) Приведенное выражение 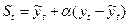используется при:

а) однопараметри­ческий методе экспоненциального сглаживания

б) двухпараметри­ческий методе экспоненциального сглаживания

в) трехпараметри­ческий методе экспоненциального сглаживания